K-均值对地图上的点进行聚类（2）

3. 对地图上的点进行聚类

示例：对于地理数据应用二分K-均值算法

(1)收集数据：使用Yahoo! placeFinder API收集数据。
(2)准备数据：只保留经纬度信息。
(3)分析数据：使用matplotlib来构建一个二维数据图，其中包含簇与地图。
(4)训练算法：训练不适用无监督学习。
(5)测试算法：使用上篇中的bikmeans（）函教。
(6)使用算法：最后的输出是包含簇及簇中心的地图。

3.1 收集数据

# -*- coding: utf-8 -*-
import urllib
import json
def geoGrab(stAddress, city): 
    apiStem = 'http://where.yahooapis.com/geocode?'  
    params = {}
    params['flags'] = 'J'  # 返回JSON
    params['appid'] = 'aaa0VN6k'
    params['location'] = '%s %s' % (stAddress, city)
    url_params = urllib.urlencode(params)  # 将params字典转换为可以通过URL进行传递的字符串格式
    yahooApi = apiStem + url_params      
    print yahooApi  # 输出URL
    c=urllib.urlopen(yahooApi)  #读取返回值
    return json.loads(c.read())  # 返回一个字典

from time import sleep
def massPlaceFind(fileName):
    fw = open('places.txt', 'w')
    for line in open(fileName).readlines():
        line = line.strip()
        lineArr = line.split('\t')  # 是以tab分隔的文本文件
        retDict = geoGrab(lineArr[1], lineArr[2]) # 读取2列和第3列
        if retDict['ResultSet']['Error'] == 0: # 检查输出字典，判断有没有出错
            lat = float(retDict['ResultSet']['Results'][0]['latitude'])  # 读取经纬度
            lng = float(retDict['ResultSet']['Results'][0]['longitude'])
            print "%s\t%f\t%f" % (lineArr[0], lat, lng)
            fw.write('%s\t%f\t%f\n' % (line, lat, lng))  # 添加到对应的行上
        else: print 'error fetching' # 有错误时不需要抽取经纬度
        sleep(1)  # 避免频繁调用API，过于频繁的话请求会被封掉
    fw.close()


geoGrab('1 VA Center', 'Augusta,ME')

Yahoo! placeFinder API：

为了使用该服务，需要注册以获得一个APIkey。具体地，需要在Yahoo！开发者网络（Http://developer.yahoo.com)中进行注册。创建一个桌面应用后会获得一个appid。需要appid来使用geocoder。一个geocoder接受给定地址，然后返回该地址对应的经纬度。

JSON：

是一种用于序列化数组和字典的文件格式。JSON是javascript object
Notation的缩写，接下来使用urllib的urlencode（）函数将创建的字典转换为可以通过URL进行传递的字符串格式。最后，打开URL读取返回值。由于返回值是json格式的，所以可以使用JSON的Python模块来将其解码为一个字典。一旦返回了解码后的字典，也就意味着成功地对一个地址进行了地理编码。

这里没能实现，只是对代码分析了下。。

3.2 对地理坐标进行聚类

# -*- coding: utf-8 -*-
from numpy import *
# K-均值聚类支持函数
def loadDataSet(fileName):      
    dataMat = []                
    fr = open(fileName)
    for line in fr.readlines():
        curLine = line.strip().split('\t')
        fltLine = map(float,curLine) 
        dataMat.append(fltLine)
    return dataMat

# 计算两个向量的欧式距离
def distEclud(vecA, vecB):
    return sqrt(sum(power(vecA - vecB, 2))) 

# 为给定数据集构建一个包含k个随机质心的集合,是以每列的形式生成的
def randCent(dataSet, k):
    n = shape(dataSet)[1]
    centroids = mat(zeros((k,n))) 
    for j in range(n):  
        minJ = min(dataSet[:,j])  # 找到每一维的最小
        rangeJ = float(max(dataSet[:,j]) - minJ) # 每一维的最大和最小值之差
        centroids[:,j] = mat(minJ + rangeJ * random.rand(k,1)) # 生成随机值
        #print centroids[:,j]
    return centroids  # 返回随机质心,是和数据点相同的结构

# k--均值聚类算法(计算质心--分配--重新计算)
def kMeans(dataSet, k, distMeas=distEclud, createCent=randCent): # k是簇的数目
    m = shape(dataSet)[0]  # 得到样本的数目
    clusterAssment = mat(zeros((m,2))) #  创建矩阵来存储每个点的簇分配结果
                                       #  第一列：记录簇索引值，第二列：存储误差，欧式距离的平方
    centroids = createCent(dataSet, k)  # 创建k个随机质心
    clusterChanged = True
    while clusterChanged:  # 迭代使用while循环来实现
        clusterChanged = False  
        for i in range(m):  # 遍历每个数据点，找到距离每个点最近的质心
            minDist = inf; minIndex = -1
            for j in range(k):  # 寻找最近的质心
                distJI = distMeas(centroids[j,:],dataSet[i,:])
                if distJI < minDist:
                    minDist = distJI; minIndex = j
            if clusterAssment[i,0] != minIndex: # 更新停止的条件
                clusterChanged = True
            clusterAssment[i,:] = minIndex,minDist**2 # minDist**2就去掉了根号         
        for cent in range(k):  # 更新质心的位置
            ptsInClust = dataSet[nonzero(clusterAssment[:,0].A==cent)[0]] 
            centroids[cent,:] = mean(ptsInClust, axis=0) # 然后计算均值，axis=0:沿列方向 
    #print 'centroids:',centroids
    return centroids, clusterAssment # 返回簇和每个簇的误差值，误差值是当前点到该簇的质心的距离

# 二分k--均值聚类算法
def biKmeans(dataSet, k, distMeas=distEclud):
    m = shape(dataSet)[0] 
    clusterAssment = mat(zeros((m,2))) # 存储数据集中每个点的簇分配结果及平方误差
    centroid0 = mean(dataSet, axis=0).tolist()[0] # 计算整个数据集的质心：1*2的向量
    centList =[centroid0] # []的意思是使用一个列表保存所有的质心,簇列表,[]的作用很大
    for j in range(m):  # 遍历所有的数据点，计算到初始质心的误差值，存储在第1列
        clusterAssment[j,1] = distMeas(mat(centroid0), dataSet[j,:])**2
    while (len(centList) < k):  # 不断对簇进行划分，直到k
        lowestSSE = inf  # 初始化SSE为无穷大
        for i in range(len(centList)): # 遍历每一个簇
            #print 'i:',i               # 数组过滤得到所有的类别簇等于i的数据集
            ptsInCurrCluster = dataSet[nonzero(clusterAssment[:,0].A==i)[0],:]
            # 得到2个簇和每个簇的误差，centroidMat：簇矩阵  splitClustAss：[索引值,误差]
            centroidMat, splitClustAss = kMeans(ptsInCurrCluster, 2, distMeas) # centroidMat是矩阵
            sseSplit = sum(splitClustAss[:,1])  # 求二分k划分后所有数据点的误差和     
                                             # 数组过滤得到整个数据点集的簇中不等于i的点集
            #print nonzero(clusterAssment[:,0].A!=i)[0]
            sseNotSplit = sum(clusterAssment[nonzero(clusterAssment[:,0].A!=i)[0],1])# 所有剩余数据集的误差之和
            #print "sseSplit and notSplit: ",sseSplit,',',sseNotSplit
            if (sseSplit + sseNotSplit) < lowestSSE: # 划分后的误差和小于当前的误差，本次划分被保存
                #print 'here..........'
                bestCentToSplit = i  # i代表簇数
                bestNewCents = centroidMat  # 保存簇矩阵
                #print 'bestNewCents',bestNewCents
                bestClustAss = splitClustAss.copy() # 拷贝所有数据点的簇索引和误差
                lowestSSE = sseSplit + sseNotSplit  # 保存当前误差和
        # centList是原划分的簇向量，bestCentToSplit是i值
        #print 'len(centList) and  bestCentToSplit ',len(centList),',',bestCentToSplit
                  # 数组过滤得到的是新划分的簇类别是1的数据集的类别簇重新划为新的类别值为最大的类别数
        bestClustAss[nonzero(bestClustAss[:,0].A == 1)[0],0] = len(centList) 
                  # 数组过滤得到的是新划分的簇类别是0的数据集的类别簇重新划为新的类别值为i
        bestClustAss[nonzero(bestClustAss[:,0].A == 0)[0],0] = bestCentToSplit
        #print 'the bestCentToSplit is: ',bestCentToSplit   # 代表的是划分的簇个数-1
        #print 'the len of bestClustAss is: ', len(bestClustAss) # 数据簇的数据点个数
                                   # 新划分簇矩阵的第0簇向量新增到当前的簇列表中
        centList[bestCentToSplit] = bestNewCents[0,:].tolist()[0] 
        #print 'centList[bestCentToSplit]:',centList[bestCentToSplit]
                        # 新划分簇矩阵的第1簇向量添加到当前的簇列表中
        centList.append(bestNewCents[1,:].tolist()[0]) # centList是列表的格式
        #print 'centList',centList
                    # 数组过滤得到所有数据集中簇类别是新簇的数据点
        clusterAssment[nonzero(clusterAssment[:,0].A == bestCentToSplit)[0],:]= bestClustAss
    return mat(centList), clusterAssment # 返回质心列表和簇分配结果


# 球面距离计算，这里是利用球面余弦定理
def distSLC(vecA, vecB):  # 经度和纬度用角度作为单位，这里用角度除以180然后乘以pi作为余弦函数的输入
    a = sin(vecA[0,1]*pi/180) * sin(vecB[0,1]*pi/180) 
    b = cos(vecA[0,1]*pi/180) * cos(vecB[0,1]*pi/180) * \
                      cos(pi * (vecB[0,0]-vecA[0,0]) /180)
    return arccos(a + b)*6371.0  # 返回地球表面两点之间的距离


import matplotlib
import matplotlib.pyplot as plt
# 及簇绘图函数 
def clusterClubs(numClust=5):  # 希望分得的簇数
    datList = []  # 创建一个空列表
    for line in open('places.txt').readlines():
        lineArr = line.split('\t')
        datList.append([float(lineArr[4]), float(lineArr[3])])  # 对应的是纬度和经度
    datMat = mat(datList) # 创建一个矩阵
    myCentroids, clustAssing = biKmeans(datMat, numClust, distMeas=distSLC)
    fig = plt.figure() # 创建一幅图
    rect=[0.1,0.1,0.8,0.8] # 创建一个矩形来决定绘制图的哪一部分
    scatterMarkers=['s', 'o', '^', '8', 'p', 'd', 'v', 'h', '>', '<'] # 构建一个标记形状的列表来绘制散点图
    axprops = dict(xticks=[], yticks=[])
    ax0=fig.add_axes(rect, label='ax0', **axprops)  # 创建一个子图
    imgP = plt.imread('Portland.png')  # imread()函数基于一幅图像来创建矩阵
    ax0.imshow(imgP) # imshow()绘制该矩阵
    ax1=fig.add_axes(rect, label='ax1', frameon=False) # 在同一张图上又创建一个字图
    for i in range(numClust): # 遍历每一个簇
        ptsInCurrCluster = datMat[nonzero(clustAssing[:,0].A==i)[0],:]
        markerStyle = scatterMarkers[i % len(scatterMarkers)]
        ax1.scatter(ptsInCurrCluster[:,0].flatten().A[0], ptsInCurrCluster[:,1].flatten().A[0], marker=markerStyle, s=90)
    ax1.scatter(myCentroids[:,0].flatten().A[0], myCentroids[:,1].flatten().A[0], marker='+', s=300)
    plt.show()    


# 主函数
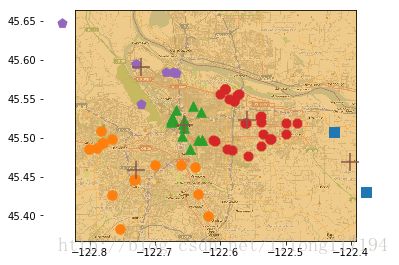
clusterClubs(5)

由于源代码里给出了从Yahoo! placeFinder API得到的数据，所以这里直接拿来用了，得到的结果：

也可以通过改变聚类簇数来查看聚类效果，在此不再演示。

4. 注意的几点：

4.1球面距离公式是计算球面上两点间距离的公式

设所求
点 A ：纬度 β1 ，经度 α1 ；
点 B ：纬度 β2 ，经度 α2 ；
则距离 S=R⋅arccos[cosβ1cosβ2cos（α1−α2）+sinβ1sinβ2]
其中 R 为球体半径。

4.2 fig.add_axes()和Subplot（）用法

ax3 = fig.add_axes([0.1, 0.1, 0.8, 0.8])  
ax4 = fig.add_axes([0.72, 0.72, 0.16, 0.16])  

这里看几个例子：

Axes - Subplot - Axis 之间的关系：

figure就是画板，是画纸的载体，但是具体画画等操作是在画纸上完成的。在pyplot中，画纸的概念对应的就是Axes/Subplot。

（1）subplot的操作

import matplotlib
import matplotlib.pyplot as plt
fig = plt.figure()  
ax = fig.add_subplot(111)  
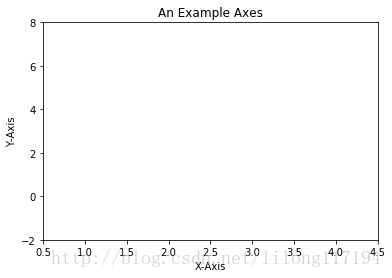
ax.set(xlim=[0.5, 4.5], ylim=[-2, 8], title='An Example Axes', ylabel='Y-Axis', xlabel='X-Axis')  
plt.show()

运行结果：

（2）Axes 和 Subplot 的区别

Axes的使用：

fig = plt.figure()  
ax3 = fig.add_axes([0.1, 0.1, 0.8, 0.8])  
ax4 = fig.add_axes([0.72, 0.72, 0.16, 0.16])  
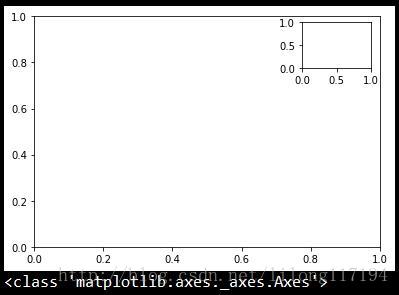
plt.show()
print type(ax3) 

运行结果：

这里轴域（Axes）可以理解成一些轴（Axis）的集合，当然这个集合还有很多轴（Axis）的属性，标注等等。

我们用add_axes()方法生成一个轴域（Axes），括号里面的值前两个是轴域原点坐标（这里指的是以整个figure为参照，前两个值是相对于figure的左下角而言的，而不是当前子图的起始坐标），后两个是显示坐标轴的长度（这里指的是子图的轴长，也是相对于figure的长度而言的）。当我们生成了轴域的时候，从结果上看确实是生成了一个可以画图的子图。

我们还可以分别在两个轴域（Axes）中画图。 对比两种方法，两种对象，我们可以总结总结： add_subplot()方法在生成子图过程，简单明了，而用add_axes()方法,则生成子图的灵活性更强，完全可以实现add_subplot()方法的功能，可以控制子图显示位置，甚至实现相互重叠的效果。下面是几个例子：

subplot

fig = plt.figure()  
ax1 = fig.add_subplot(211)  
ax2 = fig.add_subplot(212)  
plt.show()

Axes

fig = plt.figure()  
ax3 = fig.add_axes([0, 0, 0.5, 0.5], title='An Example Axes', ylabel='Y-Axis', xlabel='X-Axis')  
ax4 = fig.add_axes([0.6, 0.6, 0.2, 0.16], title='An Example Axes', ylabel='Y-Axis', xlabel='X-Axis')  
plt.show()

可以看出ax3是从画板的原点（0，0）开始画，横纵坐标轴都是0.5
ax4是从画板的（0.6，0.6）开始画，横纵坐标轴分别是0.2和0.6

fig = plt.figure()  
ax3 = fig.add_axes([0, 0, 0.3, 1], title='An Example Axes', ylabel='Y-Axis', xlabel='X-Axis')  
ax4 = fig.add_axes([0.6, 0.3, 0.2, 0.3], title='An Example Axes', ylabel='Y-Axis', xlabel='X-Axis')  
plt.show()

参考：https://www.zhihu.com/question/51745620

4.3 scatterMarkers[i % len(scatterMarkers)]

markerStyle = scatterMarkers[i % len(scatterMarkers)]

使用：

>>> scatterMarkers=['s', 'o', '^', '8', 'p', 'd', 'v', 'h', '>', '<']
>>> for i in range(5):
...     markerStyle = scatterMarkers[i % len(scatterMarkers)]
...     print markerStyle
... 
s
o
^
8
p
>>> 

类似于列表推到式，但此还有一个特殊的地方是可以循环使用，也就是更多簇时，可以循环标记。