互补滤波器

互补滤波器

从 RC 电路 到 数字滤波器 。

参考：wikiPedia

by luoshi006

原理

低通滤波器

一阶低通滤波器

传递函数

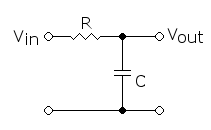
常见的 RC 电路构成的一阶低通滤波器的输入(U) 输出(Y)关系如下：

YU=11+RC⋅S Y U = 1 1 + R C ⋅ S

其中，滤波器的截止频率为： wc=1RC w c = 1 R C 。

将传函转换为微分形式：

y(t)+RCdy(t)dt=x(t) y ( t ) + R C d y ( t ) d t = x ( t )

dy(t)dt=差分=y(k)−y(k−1)Δt d y ( t ) d t = 差 分 = y ( k ) − y ( k − 1 ) Δ t ，代入得到差分形式：

y(k)=RCΔt+RCy(k−1)+ΔtΔt+RCx(k) y ( k ) = R C Δ t + R C y ( k − 1 ) + Δ t Δ t + R C x ( k )

由近似公式：

11+Δt/RC=˙1−ΔtRC 1 1 + Δ t / R C = ˙ 1 − Δ t R C

可得：

y(k)=(1−ΔtRC)y(k−1)+ΔtRCx(k) y ( k ) = ( 1 − Δ t R C ) y ( k − 1 ) + Δ t R C x ( k )

即，一阶低通滤波的差分形式。

---

二阶低通滤波

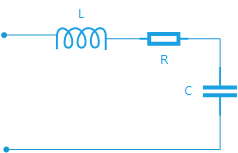
过程略；

y(k)=2(1+σΔt)1+2σΔt+ω20Δt2y(k−1)−11+2σΔt+ω20Δt2y(k−2)+ω20Δt21+2σΔt+ω20Δt2x(k) y ( k ) = 2 ( 1 + σ Δ t ) 1 + 2 σ Δ t + ω 0 2 Δ t 2 y ( k − 1 ) − 1 1 + 2 σ Δ t + ω 0 2 Δ t 2 y ( k − 2 ) + ω 0 2 Δ t 2 1 + 2 σ Δ t + ω 0 2 Δ t 2 x ( k )

其中， σ=R2L,ω20=1LC σ = R 2 L , ω 0 2 = 1 L C 。

---

高通滤波器

依然使用RC电路为模型。
传递函数为：

G(s)=11+1RC⋅S G ( s ) = 1 1 + 1 R C ⋅ S

=RC⋅SRC⋅S+1 = R C ⋅ S R C ⋅ S + 1

******************* 内容仅作参考 *******************************
由 $s=\frac {Z-1}{T}$变换：

$$U\cdot RC \cdot Z - U\cdot RC=Y\cdot RC \cdot Z- Y\cdot RC+Y\cdot T$$

Z反变换：

$$Y(k+1)=U(k+1)-U(k)+(1-\frac{T}{RC}) Y(k)$$

将传函转化为微分形式：

RC⋅dy(t)dt+y(t)=RC⋅dx(t)dt R C ⋅ d y ( t ) d t + y ( t ) = R C ⋅ d x ( t ) d t

转换为差分形式：

y(k)=RCRC+Ty(k−1)+RCRC+T(x(k)−x(k−1)) y ( k ) = R C R C + T y ( k − 1 ) + R C R C + T ( x ( k ) − x ( k − 1 ) )

---

互补滤波器

综上，可知：
低通滤波器：

y(k)=RCRC+Ty(k−1)+TRC+Tx(k) y ( k ) = R C R C + T y ( k − 1 ) + T R C + T x ( k )

高通滤波器：

y(k)=RCRC+T[y(k−1)+Δx(k)] y ( k ) = R C R C + T [ y ( k − 1 ) + Δ x ( k ) ]

故，互补滤波器：

y(k)=RCRC+T[y(k−1)+Δxgyro(k)]+TT+RCxacc(k) y ( k ) = R C R C + T [ y ( k − 1 ) + Δ x g y r o ( k ) ] + T T + R C x a c c ( k )

angle = (factor) * (angle + gyro * dt ) + (1 - factor) * (x_acc);
其中，factor 为互补滤波因子，定义域：( 0 , 1 )。

---

the end

本文简单介绍了一阶互补滤波的理论和实现，以期望对刚开始接触数字滤波的朋友有所帮助。

互补滤波使用较多的 mahony 滤波，限于篇幅，另外介绍。

如果在文中，发现错误或不妥当的地方，请直接留言，或 邮箱 交流。不胜感激~

---