基于Verilog的32位并行进位加法器设计
1、功能概述:
先行进位加法器是对普通的全加器进行改良而设计成的并行加法器,主要是针对普通全加器串联时互相进位产生的延迟进行了改良。超前进位加法器是通过增加了一个不是十分复杂的逻辑电路来做到这点的。
设二进制加法器第i位为Ai,Bi,输出为Si,进位输入为Ci,进位输出为Ci+1,则有:
Si=Ai⊕Bi⊕Ci (1-1)
Ci+1 =Ai * Bi+ Ai Ci+ BiCi =Ai * Bi+(Ai+Bi)* Ci (1-2)
令Gi = Ai * Bi , Pi = Ai+Bi,则Ci+1= Gi+ Pi *Ci
当Ai和Bi都为1时,Gi = 1, 产生进位Ci+1 = 1
当Ai和Bi有一个为1时,Pi = 1,传递进位Ci+1= Ci
因此Gi定义为进位产生信号,Pi定义为进位传递信号。Gi的优先级比Pi高,也就是说:当Gi = 1时(当然此时也有Pi = 1),无条件产生进位,而不管Ci是多少;当Gi=0而Pi=1时,进位输出为Ci,跟Ci之前的逻辑有关。
下面推导4位超前进位加法器。设4位加数和被加数为A和B,进位输入为Cin,进位输出为Cout,对于第i位的进位产生Gi = Ai·Bi ,进位传递Pi=Ai+Bi , i=0,1,2,3。于是这各级进位输出,递归的展开Ci,有:
C0 = Cin
C1=G0 + P0·C0
C2=G1 + P1·C1 = G1 + P1·G0 + P1·P0 ▪C0
C3=G2 + P2·C2 = G2 + P2·G1 + P2·P1·G0 + P2·P1·P0·C0
C4=G3 + P3·C3 = G3 + P3·G2 + P3·P2·G1 + P3·P2·P1·G0 + P3·P2·P1·P0·C0 (1-3)
Cout=C4
由此可以看出,各级的进位彼此独立产生,只与输入数据Ai、Bi和Cin有关,将各级间的进位级联传播给去掉了,因此减小了进位产生的延迟。每个等式与只有三级延迟的电路对应,第一级延迟对应进位产生信号和进位传递信号,后两级延迟对应上面的积之和。实现上述逻辑表达式(1-3)的电路称为超前进位部件(Carry Lookahead Unit),也称为CLA部件。通过这种进位方式实现的加法器称为超前进位加法器。因为各个进位是并行产生的,所以是一种并行进位加法器。
从公式(1-3)可知,更多位数的CLA部件只会增加逻辑门的输入端个数,而不会增加门的级数,因此,如果采用超前进位方式实现更多位的加法器,从理论上讲,门延迟不变。但是由于CLA部件中连线数量和输入端个数的增多,使得电路中需要具有大驱动信号和大扇入门,这会大大增加门的延迟,起不到提高电路性能的作用。因此更多位数的加法器可通过4位CLA部件和4位超前进位加法器来实现,如图2所示。
将式(1-3)中进位C4的逻辑方程改写为:
C4=Gm0 + Pm0·C0 (1-4)
C4表示4位加法器的进位输出,Pm0、Gm0分别表示4位加法器的进位传递输出和进位产生输出,分别为:
Pm0 = P3·P2·P1·P0
Gm0 = G3 + P3·G2 + P3·P2·G1 + P3·P2·P1·G0
将式(1-4)应用于4个4位先行进位加法器,则有:
C4=Gm0 + Pm0·C0
C8= Gm1 + Pm1·C4 = Gm1 + Pm1·Gm0 + Pm1·Pm0 ▪C0
C12= Gm2 + Pm2·C8 = Gm2 + Pm2·Gm1 + Pm2·Pm1·Gm0 + Pm2·Pm1·Pm0·C0
C16=Gm3+Pm3·C12=Gm3+Pm3·Gm2+Pm3·Pm2·Gm1+Pm3·Pm2·Pm1·Gm0+Pm3·Pm2·Pm1·Pm0·C0 (1-5)
比较式(1-3)和式(1-5),可以看出这两组进位逻辑表达式是类似的。不过式(1-3)表示的是组内进位,式(1-5)表示的是组间的进位。实现逻辑方程组(1-5)的电路称为成组先行进位部件。图1a为所设计的32位超前进位加法器的结构框图,该加法器采用三级超前进位加法器设计,组内和组间均采用超前进位。由8个4位超前进位加法器与3个BCLA部件构成。图1b为采用超前进位和进位选择实现的32位先行进位加法器结构图。
//一位全加器
module adder(X,Y,Cin,F,Cout);
input X,Y,Cin;
output F,Cout;
assign F = X ^ Y ^ Cin;
assign Cout = (X ^ Y) & Cin | X & Y;
endmodule
//一位全加器测试代码
`timescale 1ns/1ns
module adder_tb;
reg x;
reg y;
reg cin;
wire f;
wire cout;
adder adder(
.X(x),
.Y(y),
.Cin(cin),
.F(f),
.Cout(cout)
);
initial begin
x = 0;
y = 0;
cin = 0;
#5 x = 0;y = 1;cin = 1;
#5 x = 1;y = 0;cin = 1;
#5 x = 1;y = 0;cin = 0;
end
endmodule
/******************4位CLA部件************************/
module CLA(c0,c1,c2,c3,c4,p1,p2,p3,p4,g1,g2,g3,g4);
input c0,g1,g2,g3,g4,p1,p2,p3,p4;
output c1,c2,c3,c4;
assign c1 = g1 ^ (p1 & c0),
c2 = g2 ^ (p2 & g1) ^ (p2 & p1 & c0),
c3 = g3 ^ (p3 & g2) ^ (p3 & p2 & g1) ^ (p3 & p2 & p1 & c0),
c4 = g4 ^ (p4 & g3) ^ (p4 & p3 & g2) ^ (p4 & p3 & p2 & g1) ^(p4 & p3 & p2 & p1 & c0);
endmodule
//四位并行进位加法器
module adder_4(x,y,c0,c4,F,Gm,Pm);
input [4:1] x;
input [4:1] y;
input c0;
output c4,Gm,Pm;
output [4:1] F;
wire p1,p2,p3,p4,g1,g2,g3,g4;
wire c1,c2,c3;
adder adder1(
.X(x[1]),
.Y(y[1]),
.Cin(c0),
.F(F[1]),
.Cout()
);
adder adder2(
.X(x[2]),
.Y(y[2]),
.Cin(c1),
.F(F[2]),
.Cout()
);
adder adder3(
.X(x[3]),
.Y(y[3]),
.Cin(c2),
.F(F[3]),
.Cout()
);
adder adder4(
.X(x[4]),
.Y(y[4]),
.Cin(c3),
.F(F[4]),
.Cout()
);
CLA CLA(
.c0(c0),
.c1(c1),
.c2(c2),
.c3(c3),
.c4(c4),
.p1(p1),
.p2(p2),
.p3(p3),
.p4(p4),
.g1(g1),
.g2(g2),
.g3(g3),
.g4(g4)
);
assign p1 = x[1] ^ y[1],
p2 = x[2] ^ y[2],
p3 = x[3] ^ y[3],
p4 = x[4] ^ y[4];
assign g1 = x[1] & y[1],
g2 = x[2] & y[2],
g3 = x[3] & y[3],
g4 = x[4] & y[4];
assign Pm = p1 & p2 & p3 & p4,
Gm = g4 ^ (p4 & g3) ^ (p4 & p3 & g2) ^ (p4 & p3 & p2 & g1);
endmodule
//四位并行进位加法器测试代码
`timescale 1ns/1ns
module adder_4_tb;
reg [4:1] x;
reg [4:1] y;
reg c0;
wire c4;
wire [4:1] F;
integer i,j;
adder_4 adder_4(
.x(x),
.y(y),
.c0(c0),
.c4(c4),
.F(F),
.Pm(),
.Gm()
);
initial begin
x = 4'd0; y = 4'd0; c0 = 0;
#5;
for (i = 0; i < 16; i = i + 1)begin
for (j = 0 ; j < 16; j = j + 1) begin
y = y + 1;
#5;
end
x = x + 1;
#5;
end
#5; c0 = 1; x = 4'd0; y = 4'd0;
for (i = 0; i < 16; i = i + 1)begin
for (j = 0 ; j < 16; j = j + 1) begin
y = y + 1;
#5;
end
x = x + 1;
#5;
end
$stop;
end
endmodule
//16位CLA部件
module CLA_16(A,B,c0,S,px,gx);
input [16:1] A;
input [16:1] B;
input c0;
output gx,px;
output [16:1] S;
wire c4,c8,c12;
wire Pm1,Gm1,Pm2,Gm2,Pm3,Gm3,Pm4,Gm4;
adder_4 adder1(
.x(A[4:1]),
.y(B[4:1]),
.c0(c0),
.c4(),
.F(S[4:1]),
.Gm(Gm1),
.Pm(Pm1)
);
adder_4 adder2(
.x(A[8:5]),
.y(B[8:5]),
.c0(c4),
.c4(),
.F(S[8:5]),
.Gm(Gm2),
.Pm(Pm2)
);
adder_4 adder3(
.x(A[12:9]),
.y(B[12:9]),
.c0(c8),
.c4(),
.F(S[12:9]),
.Gm(Gm3),
.Pm(Pm3)
);
adder_4 adder4(
.x(A[16:13]),
.y(B[16:13]),
.c0(c12),
.c4(),
.F(S[16:13]),
.Gm(Gm4),
.Pm(Pm4)
);
assign c4 = Gm1 ^ (Pm1 & c0),
c8 = Gm2 ^ (Pm2 & Gm1) ^ (Pm2 & Pm1 & c0),
c12 = Gm3 ^ (Pm3 & Gm2) ^ (Pm3 & Pm2 & Gm1) ^ (Pm3 & Pm2 & Pm1 & c0);
assign px = Pm1 & Pm2 & Pm3 & Pm4,
gx = Gm4 ^ (Pm4 & Gm3) ^ (Pm4 & Pm3 & Gm2) ^ (Pm4 & Pm3 & Pm2 & Gm1);
endmodule
//32位并行进位加法器顶层模块
module adder32(A,B,S,C32);
input [32:1] A;
input [32:1] B;
output [32:1] S;
output C32;
wire px1,gx1,px2,gx2;
wire c16;
CLA_16 CLA1(
.A(A[16:1]),
.B(B[16:1]),
.c0(0),
.S(S[16:1]),
.px(px1),
.gx(gx1)
);
CLA_16 CLA2(
.A(A[32:17]),
.B(B[32:17]),
.c0(c16),
.S(S[32:17]),
.px(px2),
.gx(gx2)
);
assign c16 = gx1 ^ (px1 && 0), //c0 = 0
C32 = gx2 ^ (px2 && c16);
endmodule
`timescale 1ns/1ns
module adder32_tb;
reg [32:1] A;
reg [32:1] B;
wire [32:1] S;
wire c32;
adder32 adder32(
.A(A),
.B(B),
.S(S),
.C32(c32)
);
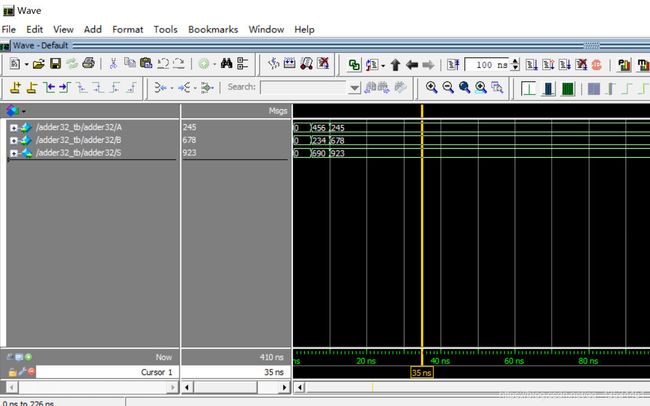
initial begin
A = 32'd0; B = 32'd0;
#5; A = 32'd 456; B = 32'd234;
#5; A = 32'd 245; B = 32'd678;
$stop;
end
endmodule