栈和队列经典题目汇总
实现一个栈,要求实现Push(出栈)、Pop(入栈)、Min(返回最小值的操作)的时间复杂度为O(1)
1.用两个栈实现
入栈:一个栈作为数据栈,一个栈作为最小值栈,往数据栈中直接压入数据,比较此时数据栈栈顶元素和min栈栈顶元素的大小,若min栈的栈顶元素小,则往min栈中压入栈顶元素,若要数据栈栈顶元素小,则压入数据栈栈顶元素。
出栈:数据栈和min栈同时pop
取最小值:取min栈的栈顶元素
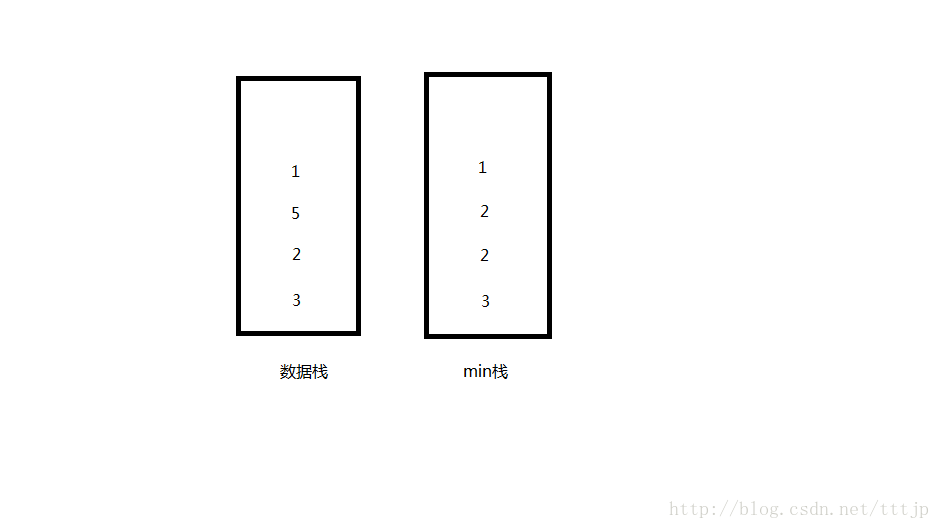
//用两个栈实现
template<class T>
class Stack1
{
public:
void Push(T d)
{
sData.push(d);
if (sMin.empty() || sMin.top() > d)
sMin.push(d);
else
sMin.push(sMin.top());
}
void Pop()
{
if (!sData.empty())
{
sData.pop();
sMin.pop();
}
else
return;
}
T& Min()
{
assert(!sMin.empty());
return sMin.top();
}
private:
stack2.用一个栈实现
入栈:min值的确定方法和两个栈时一样,不过数据和min值压入同一个栈,数据先压入,min值后压入。
出栈:pop两次。
取最小值:取栈顶元素值。

//用一个栈实现
template<class T>
class Stack2
{
public:
void Push(T d)
{
if (s.empty() || s.top() > d)
{
s.push(d);
s.push(d);
}
else
{
T tmp = s.top();
s.push(d);
s.push(tmp);
}
}
void Pop()
{
if (!s.empty())
{
s.pop();
s.pop();
}
else
return;
}
T& Min()
{
assert(!s.empty());
return s.top();
}
private:
stackpush和pop都只进行了常数次,所以时间复杂度为O(1)
使用两个栈实现一个队列
1.保证在整个过程中,一个栈为空,则另外一个栈要么为空,要么有数据,不能出现两个栈同时有数据的情况,这样就可以借助为空的那个栈进行push和pop等操作了。
template<class T>
class Queue1
{
public:
void Push(T d)
{
if (s1.empty() && s2.empty())
{
s1.push(d);
}
else if (!s1.empty() && s2.empty())
{
s1.push(d);
}
else
{
s2.push(d);
}
}
void Pop()
{
if (!s1.empty() && s2.empty())
{
while (!s1.empty()) //把所有的数放到s2中去
{
s2.push(s1.top());
s1.pop();
}
s2.pop(); //真正要删除的那个数
while (!s2.empty()) //把剩下的数放回s1中
{
s1.push(s2.top());
s2.pop();
}
}
else if (s1.empty() && !s2.empty())
{
while (!s2.empty()) //把所有的数放到s1中去
{
s1.push(s2.top());
s2.pop();
}
s1.pop(); //真正要删除的那个数
while (!s1.empty()) //把剩下的数放回s2中
{
s2.push(s1.top());
s1.pop();
}
}
else
return;
}
T& Front()
{
assert(!s1.empty() || !s2.empty());
if (!s1.empty() && s2.empty())
{
while (!s1.empty()) //把所有的数放到s2中去
{
s2.push(s1.top());
s1.pop();
}
T top = s2.top(); //保存队头
while (!s2.empty()) //把所有的数放回s1中
{
s1.push(s2.top());
s2.pop();
}
return top;
}
else if (s1.empty() && !s2.empty())
{
while (!s2.empty()) //把所有的数放到s1中去
{
s1.push(s2.top());
s2.pop();
}
T top = s1.top(); //保存队头
while (!s1.empty()) //把所有的数放回s2中
{
s2.push(s1.top());
s1.pop();
}
return top;
}
}
T& Back()
{
assert(!s1.empty() || !s2.empty());
if (!s1.empty() && s2.empty())
{
return s1.top();
}
else if (s1.empty() && !s2.empty())
{
return s2.top();
}
}
bool Empty()
{
return s1.empty() && s2.empty();
}
size_t Size()
{
return s1.size() + s2.size();
}
private:
stack s1;
stack s2;
}; 2.确保其中一个栈只能push,另一个栈只能pop
template<class T>
class Queue2
{
public:
void Push(T d)
{
sIn.push(d);
}
void Pop()
{
if (sOut.empty())
{
while (!sIn.empty())
{
sOut.push(sIn.top());
sIn.pop();
}
sOut.pop(); //队列真正要删除的数
}
else
{
sOut.pop();
}
}
T& Front()
{
assert(!sIn.empty() || !sOut.empty());
if (sOut.empty())
{
while (!sIn.empty())
{
sOut.push(sIn.top());
sIn.pop();
}
return sOut.top(); //保存队头
}
else
{
return sOut.top(); //保存队头
}
}
T& Back()
{
assert(!sIn.empty() || !sOut.empty());
if (!sIn.empty())
{
return sIn.top();
}
else
{
while (!sOut.empty())
{
sIn.push(sOut.top());
sOut.pop();
}
return sIn.top();
}
}
bool Empty()
{
return s1.empty() && s2.empty();
}
size_t Size()
{
return s1.size() + s2.size();
}
private:
stack使用两个队列实现一个栈
template<class T>
class Stack
{
public:
void Push(T d)
{
if (!q1.empty() && !q2.empty())
{
q1.push(d);
}
else if (!q1.empty() && q2.empty())
{
q1.push(d);
}
else
{
q2.push(d);
}
}
void Pop()
{
if (!q1.empty() && q2.empty())
{
while (q1.size() != 1)
{
q2.push(q1.front());
q1.pop();
}
q1.pop(); //栈真正要删除的数
}
else if (q1.empty() && !q2.empty())
{
while (q2.size() != 1)
{
q1.push(q2.front());
q2.pop();
}
q2.pop(); //栈真正要删除的数
}
else
return;
}
T& Top()
{
assert(!q1.empty() || !q2.empty());
if (!q1.empty() && q2.empty())
{
return q1.back();
}
else if (q1.empty() && !q2.empty())
{
return q2.back();
}
}
bool Empty()
{
return q1.empty() && q2.empty();
}
size_t Size()
{
return q1.size() + q2.size();
}
private:
queue元素出栈、入栈顺序的合法性。如入栈的序列(1,2,3,4,5),出栈序列为(4,5,3,2,1)
bool IsPopOrder(const int *pPush, const int *pPop, int pushSize, int popSize)
{
assert(pushSize == popSize);
stack<int> s;
int i = 0;
int j = 0;
//1.把入栈序列中的元素压入栈,直至栈顶的数等于出栈序列的元素
for (i = 0; i < pushSize; i++)
{
s.push(pPush[i]);
//2.栈顶的数等于出栈序列的元素时,弹出栈顶元素
while (!s.empty() && s.top() == pPop[j])
{
s.pop();
++j;
}
}
//3.若栈为空,则序列合法
return s.empty() == 1 ? true : false;
}一个数组实现两个栈
1.栈1用数组的奇数位实现,栈2用数组的偶数位实现。
2.把数组的中间位置当做栈底,栈1的栈顶朝左走,栈2的栈顶朝右走。
3.数组首元素位置作为栈1的栈底,数组尾元素位置作为栈2的栈底,栈1和栈2的栈顶都朝数组的中间走。
当栈1和栈2的数据个数相差较大时,第一种方法和第二种方法都会浪费数组空间,而第三种方法可以避免空间的浪费,故在此只实现第三种方法。
template
class TwoStack
{
public:
TwoStack()
:_arr(NULL)
, _top1(0)
, _top2(0)
, _capacity(0)
{
_CreateStack();
}
~TwoStack()
{
if (_arr)
delete[] _arr;
}
void Push1(const T& d)
{
_CheckCapacity();
_arr[_top1] = d; //从0号位置放元素,_top1指向下一个未放元素的位置
_top1++;
}
void Push2(const T& d)
{
_CheckCapacity();
_arr[_top2] = d; //从_capacity-1号位置放元素,_top2指向下一个未放元素的位置
_top2--;
}
void Pop1()
{
if (_top1 > 0)
{
_top1--;
}
}
void Pop2()
{
if (_top2 < _capacity - 1)
{
_top2++;
}
}
T& Top1()
{
if (_top1 > 0)
return _arr[_top1-1];
}
T& Top2()
{
if (_top2 < _capacity - 1)
return _arr[_top2+1];
}
size_t Size1()
{
return _top1;
}
size_t Size2()
{
return _capacity - 1 - _top2;
}
bool Empty1()
{
return _top1 == 0;
}
bool Empty2()
{
return _top2 == _capacity-1;
}
void Print1()
{
for (int i = 0; i < _top1; i++)
{
cout << _arr[i] << " ";
}
cout << endl;
}
void Print2()
{
for (int i = _capacity - 1; i > _top2; i--)
{
cout << _arr[i] << " ";
}
cout << endl;
}
protected:
void _CreateStack()
{
if (_arr == NULL)
{
_capacity = 3;
_arr = new T[_capacity];
//对数组进行初始化
for (int i = 0; i < _capacity; i++)
{
_arr[i] = 0;
}
_top1 = 0;
_top2 = _capacity - 1;
}
}
void _CheckCapacity()
{
if (_top1 == _top2)
{
size_t oldCapacity = _capacity;
_capacity *= 2;
T* tmpArr = new T[_capacity];
//栈1的数据正着拷
for (size_t i = 0; i < _top1; i++)
{
tmpArr[i] = _arr[i];
}
//栈2的数据倒着拷
size_t j = _capacity - 1;
for (size_t i = oldCapacity - 1; i>_top2; i--)
{
tmpArr[j] = _arr[i];
j--;
}
delete[] _arr;
_arr = tmpArr;
_top2 += _capacity / 2;
}
}
protected:
T* _arr; //数组
size_t _top1; //栈1的栈顶
size_t _top2; //栈2的栈顶
size_t _capacity; //数组的容量
};