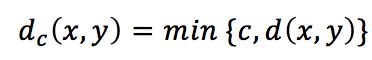OSPA距离

OSPA（Optimal Sub-patten Assignment) 最优次模式分配。

 

2019.1.17

考虑两个集合X={x1,x2,⋯,xm}和Y={y1,y,⋯,yn}。其中，n,m∈N0={0,1,⋯}。向量x∈X和y∈Y是状态空间W∈RN的子集。X,Y∈F(W)代表集合W所有有限子集的集合。OSPA度量标准定义为在χ=F(W)上的距离。

在向量x,y∈X中，引入截止距离：

其中，c>0是截止距离的一个相关参数，代表最小截止距离，表示x和y之间的距离在c处截断。

截止参数c和阶数1≤p≤∞的条件下，OSPA距离表示为：

其中，Πn代表从集合｛１，２，…，”冲取出ｍ个元素进行排列 的集合。

将称为带有截止c的p阶的OSPA度量。其中OSPA为最优子模式分配。若m=n=0，则为0。

 

原---

OSPA是一种目标跟踪系统整体性能评价的一致性度量方法，在系统状态空间上定义一种测度距离，可以用来衡量真实航迹和估计航迹之间的误差大小。

OSPA距离可将真实航迹和估计航迹之间的误差分离成两个部分，包括距离误差和关联误差。 在误差分离的基础上，该距离测度还采用了两个可调参数，即距离敏感性参数ｐ和关联敏感性参数ｃ。

距离敏感性参数ｐ(1<=ｐ<=∞ ）

可调整OSPA对于真实点集和估计点集之间距离误差的权重。在c固定不变的情况下，p的取值越大，由状态估计算法引起的位置估计偏差也会被阶数p放大，则距离相对于位置估计误差的权重得到提升。

关联敏感性参数ｃ(c>0)

可调整OSPA距离对于真实点集和估计点集之间数量不同的关联误差权重。在p固定不变的情况下，c的取值越大，由航迹起始、数据关联引起的点集数量误差会被系数c放大，因此距离，相对于点迹数量不对应的权重会得到提升。

参数调节

敏感参数p和c的取值在实际工作中采取方式简单：固定其中一个参数，调整另一个参数，从而调整某部分误差权重，综合使敏感幅值更明显。

 

参考文献

[1]D. Schuhmacher, B.-T. Vo, and B.-N. Vo, “A consistent metric for performance evaluation of multi-object filters,” IEEE Trans. Signal Processing, vol. 56, no. 8, pp. 3447–3457, Aug. 2008.

[2] 程华, 杜思伟, 林家骏. 估计融合算法的一类敏感指标研究[J]. 计算机与数字工程, 2013, 41(2):198-200.

[3] 刘国营, 陈秀宏. 多目标跟踪算法的最优子模式分配概率度量[J]. 计算机工程, 2013, 39(5):293-296.