浅谈傅里叶

最近看了一些傅里叶变换频谱的理论，由于之前学校开的课程太烂了（教材都是盗印的，理论讲的一塌糊涂）导致这部分学的其实不好。后来根据另一位老师所上的Matlab课程，讲了一些的傅里叶知识，让我才算有些懂了，在这里跟大家分享，也算我自己总结一遍，有谬误之处欢迎指正呀o(￣▽￣)ブ。

1.傅里叶级数

要讲傅里叶，就必须先从傅里叶级数开始讲起。想必大家在高数或者数分课上都讲过，就是将周期信号分解为傅里叶级数。这其中两点要注意。第一，周期信号才能分解成离散的级数，而这本身就是傅里叶积分在特定条件下的一种简化。第二，按照下面的公式。

$x\left(t\right)=\frac{a_0}{2}+{\sum }_{n=1}^{\infty }\left(a_n\cos \left(n{\omega }_{0}t\right)+b_n\sin \left(n{\omega }_{0}t\right)\right)$

啊啊啊手打LateX公式好累，我就贴图了，有没有简单点的方法啊啊啊啊）

其中的${\omega }_0$就是原周期函数的频率。可见这样分解出来的频率是有俩个，一个$a_n$，一个$b_n$，这两个都是实数，即傅里叶变换后应该是两个独立的变量的。
根据欧拉公式，将上述公式可以变为复数形式，公式如下。

这里很重要的提醒，时刻注意这个$c_n$是个复数，也就是仍有2个自由度，虚部和实部是两个独立的变量。

2.傅里叶变换

对于非周期性函数，显然它的分解不可能按照级数，因为周期的函数一直累加怎么也不会变成非周期的啊。所以显然要用积分的方法。原先离散的频率变成连续的，就形成了频谱，公式如下。

反变换如下。

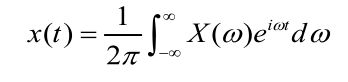
这里再添加一个帕斯瓦尔定理

很显然，帕斯瓦尔定理描述的是一种能量的守恒，即频域和时域的能量是相同的。因为很显然，积分的时候$e^{-i\omega t}$无论t和$\omega$取多少，模都是1，因此能量不会增减。
但是，很重要的一点是，这里积分出来后，频谱$X(\omega )$依然是一个复数，也就是还是有两个独立的变量，实部和虚部，也即幅值和相位。我们平常所说的频谱，大多是指，$X(\omega )$幅值和频率的关系。
显然，通过上述的关系式，可见傅里叶级数其实是傅里叶变换的一种特殊形式，因为当原函数$x(t)$为周期函数的时候，按照傅里叶变换后$X(\omega )$只有在几个倍频上才可能不为零，否则在其他不是倍频的时候，函数值是一定为0的。即，傅里叶级数只是傅里叶变换在原函数是周期函数时的一种特殊形式。
再提醒一点，当频率用$\omega$（或者叫角频率）表示时，前面会多一个$2\pi$为系数，当频率用f表示时，就没有这个系数。

这里特别提一个函数，$\delta (t)$函数。这个函数如下。

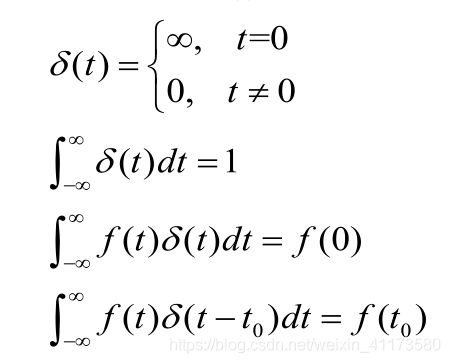
根据上述公式，我们对$\delta (t)$函数做傅里叶变换，很显然就有如下性质。

$$F[\delta (t)]={\int }_{-\infty }^{\infty }\delta (t)e^{-i\omega t}dt=1$$

这里之所以提到$\delta$函数，是因为这个函数我们即将用到，这个即将，是指下一节。

自从傅里叶傅老师发明这个东西以来，大家都惊呼，哇这个东西好用啊，很多东西时域上乱七八糟，但是频域上反而特征鲜明，所以得到了广泛的应用，尤其是工程上。

3.离散傅里叶变换（DFT)

但是一用到工程上，攻城狮们就又觉得不大趁手，因为傅里叶变换针对的是一个时域上连续的函数，这个函数式还得已知。但是工程上，采集信号肯定是一个一个点采集的，举个离子，比如设定好采样频率如100 Hz，那么你1秒只内就只能采100个点，也即每隔0.01秒采集一个点。因此也根本不可能得到一个连续的信号的，更遑论得到这个信号的表达式了。（废话这个表达式往往根本就没有，难道要插值？还是拟合？是不是在觉得我在逗你笑？）
既然得到的信号是离散的点，且不知道表达式，这个信号我们该怎么样分析频谱呢？
这个时候傅老师呵呵一笑：“你以为离散的点我就拿你没招了吗。没了我，还有离散傅里叶变换（DFT, Discrete Fourier Transform)。”这个时候就请出我们上文提到的$\delta (t)$函数。
假设这个信号的原函数是$x(t)$，那么我们每隔$\Delta t$取一个点，那么总共过了$N\Delta t$的时间，取了$N$个点。假设从0时刻开始，那么我们所取的信号就分别是：
$$x(0),x(\Delta t),x(2\Delta t),x(3\Delta t)...x((N-1)\Delta t)$$。注意，这里我们仅以$x(t)$表示这个连续的函数，我们依旧是不知道这个函数的具体表达式的，但是通过$\delta (t)$函数，我们可以将这些测量得到的点这样表示：
$$x(t)\delta (t-0),x(t)\delta (t-\Delta t),x(t)\delta (t-2\Delta t),x(t)\delta (t-3\Delta t)...x(t)\delta (t-(N-1)\Delta t)$$
(这里很重要?）

也即，这一串离散的信号可以表示为

$$\sum _{n=0}^{N-1}x(t)\delta (t-n\Delta t)$$

注意，通过这样的手段，这一串离散的信号就被这样表示成了上面这个连续的函数。既然连续了，不就可以进行傅里叶了？【滑稽】

那么这样推导，傅里叶变换之后的结果如下。为方便起见，我们这里将频域的自变量换为$f$。

$$X(f)={\int }_{-\infty }^{\infty }\sum _{n=0}^{N-1}x(t)\delta (t-n\Delta t)e^{-i2\pi ft}dt$$

根据我以前数分里学的，好像是原函数满足一致连续的条件就可以把积分号和求和号互换（这条定理我忘了，应该有误，有人提醒的话，或者以后看书，一定改正）。一般情况下我们的信号什么条件都满足，那么我们就可以得到。

$$X(f)=\sum _{n=0}^{N-1}{\int }_{-\infty }^{\infty }x(t)\delta (t-n\Delta t)e^{-i2\pi ft}dt=\sum _{n=0}^{N-1}x(n\Delta t)e^{-i2\pi fn\Delta t}$$

根据上述公式，我们就可以画出一个频谱来，而且这个频谱还是连续的，即每一个$f$都可以计算出一个相对应的而且还可能不为零的$X(f)$。但是是不是说我们这样就可以随便取频率呢？首先，由于总时长$T=N\delta t$是一定的，那么采样频率的分辨率就只有$\Delta f=1/T$。也即，从0开始，我们所能分辨的最小频率为$\Delta f$。因此，实际上我们能得到的还是一个离散的频谱，这个频谱如下,$f_k=\frac{k}{T}=\frac{k}{N\Delta t}$，其中$k=0,1,2,3,...N-1$。

$$X_k=X(f_k)=\sum _{n=0}^{N-1}x(n\Delta t)e^{-i2\pi f_{k}n\Delta t}=\sum _{n=0}^{N-1}{x}_n{e}^{-i2\pi nk/N}$$

这样绕来绕去，我们就得到了一个离散的频谱。显然上式最右端，已经可以整理成一个跟频率没有关系，而是跟总数N有关系的式子，为了方便区分大小x，用y表示频谱，即上图的$X$，（这也是为了跟Matlab匹配）这样我们可以写成如下形式。
$$\begin{array}{l}\left[\begin{array}{c}{y}_0\\ y_1\\ y_2\\ ⋮\\ y_{n-1}\end{array}\right]=\left[\begin{array}{ccccc}{\omega }^0& {\omega }^0& {\omega }^0& \cdots & {\omega }^0\\ {\omega }^0& {\omega }^1& {\omega }^2& \cdots & {\omega }^{n-1}\\ {\omega }^0& {\omega }^2& {\omega }^4& \cdots & {\omega }^{2(n-1)}\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ {\omega }^0& {\omega }^{n-1}& {\omega }^{2(n-1)}& \cdots & {\omega }^{{(n-1)}^2}\end{array}\right]\left[\begin{array}{c}{x}_0\\ x_1\\ x_2\\ ⋮\\ x_{n-1}\end{array}\right]\\ \end{array}$$
（我靠LateX手打公式真的累）
其中$\omega =e^{-i2\pi /n}$，不信的可以自己把这个矩阵算算，拆开看看是不是上面那个求和的式子【滑稽*2】。上面那个庞大的矩阵就是著名的傅里叶矩阵，根据这一个矩阵，我们就能得到这样的左侧这样一个矩阵列，这就是我们所要的频谱。

等下，慢着。好像哪里不对。我们这样进行变换之后，所能得到的频谱共有N个数，但是频谱的分辨率是$\Delta f=1/T=1/N\Delta t$，那么所能得到的频谱的最大值就是$f_{max}=1/\Delta t=f_s$。而根据Nyquist采样定理，要求$f_{max}=f_s/2$。也就是说频谱中频率大于$f_s$的部分就会发生混叠，是不可信的，只有频谱的前一半是可用的，因此必须去掉后一半。
值得注意的是，这里得到的频谱$y_k$依旧是复数，也就是两个自由度的，有实部和虚部两个变量，因此我们通常关注的频谱就是$y_k$的绝对值频率与$f$的关系。

4. 快速傅里叶变换(FFT)

其实到这里，上面的DFT已经能够解决工程上的大部分问题了，唯一的缺点是，计算量比较大，这是因为工程上采样率往往较高，有时会达到几万赫兹，因此产生的数据量巨大，矩阵乘法太慢了。由于这个傅里叶矩阵非常有特点，因此会有很多数学上的技巧进行快速的计算，因此就产生了快速傅里叶变换，也就是说没有什么新东西，只是一些数学上加快计算的技巧罢了。
限于我是个咸鱼，也是由于篇幅有限，这里就不介绍这种技巧了（实际上我也不知道）。
下面我们讲讲Matlab里的fft函数的用法，主要是来看看该怎样快速的生成一个离散信号的频谱。

Fs = 1000;            % Sampling frequency                    
T = 1/Fs;             % Sampling period       
L = 1500;             % Length of signal
t = (0:L-1)*T;        % Time vector

然后随便生成了个信号X。利用fft函数，代码如下。

Y = fft(X);
P2 = abs(Y/L);
P1 = P2(1:L/2+1);
P1(2:end-1) = 2*P1(2:end-1);

f = Fs*(0:(L/2))/L;
plot(f,P1) 
title('Single-Sided Amplitude Spectrum of X(t)')
xlabel('f (Hz)')
ylabel('|P1(f)|')

其中Y/L（L就是采样的总点数）是一种归一化的表现，是为了使得频谱信号的幅值不会随着采样点数的增加而增加。最后P1只取了P2的一半，这就是如上文所说，摒弃了超过$f_s/2$的部分。

好啦，这一次把我目前想清楚的部分都给大家交代啦，有什么疑问和指正，欢迎大家随时和我讨论呀，开心★,°:.☆(￣▽￣)/$:.°★ 。