为什么要停止过度使用置换重要性来寻找影响特征
数据分析师通常为了某些任务需要计算特征重要度。特征重要度可以帮助使用者了解数据中是否存在偏差或者模型中是否存在缺陷。并且特征重要度可用于理解底层流程和做出业务决策。模型最重要的特性可能会给我们进一步的特征工程提供灵感。
目前计算特征重要性的方法有很多种。其中一些方法基于特定的模型,例如线性回归模型中的回归系数、基于树的模型中的增益重要性或神经网络中的批处理范数参数(批处理参数通常用于NN pruning,即神经网络剪枝压缩)。其他一些方法是“通用的”,它们几乎可以应用于任何模型: SHAP 值、置换重要性(permutaion importance)、删除和重新学习方法(drop-and-relearn approach)等。
尽管机器学习模型的黑箱可解释性是模型开发研究的一个重要组成部分,但是Harmanpreet等人的一项研究显示,并非所有的数据分析师和科学家都知道如何正确地解释模型。这些方法的有效性和易用性使得它们几乎成为不二选择。实际上,如果可以通过运行pip install lib, lib.explain(model)来解决问题,为什么还要费心具体的理论呢。
在这篇文章中,主要想要说明一个认知偏差,即过度使用置换重要性来寻找影响特征。本文将说明在某些情况下,置换重要性给出了错误的、误导性的结果。
置换重要性(Permutation Importance)
置换重要性是一种常用的特征重要性类型。其核心思想在于:如果用随机排列的值替换特征,会导致模型分数的下降。它是通过几个简单的步骤来计算的:
- 使用训练数据集(X_train,y_train)来训练模型;
- 对训练数据集进行预测(X_train,y_hat),计算准确度得分(
score, 得分越高越好); - 计算每个特征(feature_i)的置换重要性:
- (1) 置换训练数据集中的第
i个特征的值(feature_i),保持其它特征不变。生成置换后的训练数据集(X_train_permuted); - (2) 用第2步训练好的模型以及X_train_permuted数据集进行预测(y_hat_permuted);
- (3)计算对应的准确度得分(score_permuted);
- (4)每个特征的置换重要性即为对应的差异系数(
score_permuted - score)。
- 上述步骤重复若干次并取平均值,以避免随机置换的不确定性影响。
用于说明计算的代码如下:
def calculate_permutation_importance(
model,
X: pd.DataFrame,
y: pd.Series,
scoring_function: Callable = sklearn.metrics.roc_auc_score,
n_repeats: int = 3,
seed: int = 42,
) -> Tuple[any, float, Dict[str, float], np.array]:
"""
Example of permutation importance calculation
:param model: sklearn model, or any model with `fit` and `predict` methods
:param X: input features
:param y: input target
:param scoring_function: function to use for scoring, should output single float value
:param n_repeats: how many times make permutation
:param seed: random state for experiment reproducibility
:return:
"""
# step 1 - train model
model.fit(X, y)
# step 2 - make predictions for train data and score (higher score - better)
y_hat_no_shuffle = model.predict(X)
score = scoring_function(*(y, y_hat_no_shuffle))
# step 3 - calculate permutation importance
features = X.columns
items = [(key, 0) for key in features]
importances = collections.OrderedDict(items)
for n in range(n_repeats):
for col in features:
# copy data to avoid using previously shuffled versions
X_temp = X.copy()
# shuffle feature_i values
X_temp[col] = X[col].sample(X.shape[0], replace=True, random_state=seed+n).values
# make prediction for shuffled dataset
y_hat = model.predict(X_temp)
# calculate score
score_permuted = scoring_function(*(y, y_hat))
# calculate delta score
# better model <-> higher score
# lower the delta -> more important the feature
delta_score = score_permuted - score
# save result
importances[col] += delta_score / n_repeats
importances_values = np.array(list(importances.values()))
importance_ranks = rank_array(importances_values)
return model, score, importances, importance_ranks
置换重要性很容易解释、实现和使用。虽然计算需要对训练数据进行n_features次预测,但与模型再训练或精确SHAP值计算相比,置换重要性不需要大量的重新计算。此外,置换重要性允许选择特征:如果置换数据集上的分数高于正常数据集,那么就表明应该删除该特征并重新训练模型。基于这些原因,置换重要性在许多机器学习项目中得到了广泛的应用。
存在的问题
虽然置换重要性是一个非常有吸引力的模型解释选择,但它有几个问题,特别是在特征具有一定相关性关系时。Giles Hooker和Lucas Mentch在他们的论文https://arxiv.org/abs/1905.03151中阐述如下:
- Strobl等人(2007)注意到在CART-builded树中置换重要性度量偏向于与其他特征相关和/或具有多个类别的特征,并进一步表明bootstrapping增强了这一影响效果;
- Archer和Kimes(2008)探讨了类似的问题,并注意到当真正的特征(那些与响应相关的特征)与噪声特征不相关时,置换重要性判断性能得到改善;
- Nicodemus等人(2010)在一个大规模的模拟研究中开展调查,并再次发现置换重要性方法高估了相关预测因子的重要性。
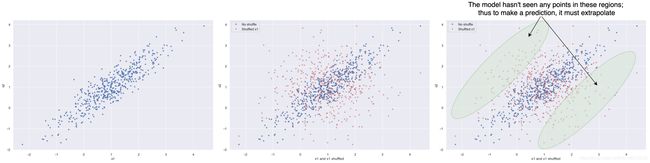
对这一问题可能的解释是模型的外推性能。假设模型是使用两个高度正相关的特征x1和x2(下图中的左图)进行训练的。为了计算特征x1的重要性,我们对特征进行随机化处理,并对“随机”点(中心图上的红色点)进行预测。但这个模型在左上角和右下角都没有看到x1的任何训练例子。因此,要做出预测,它必须外推到以前看不见的区域(右图)。我们知道,所有模型的外推性能都很糟糕,因此做出了出乎意料的预测。这些“来自新区域的分数”强烈影响最终分数,当然也影响置换重要性。
Giles Hooker和Lucas Mentch提出了几种替代方法来代替置换重要性:
- 约束置换重要性——有条件地置换特征,基于剩余特征的值来避免“看不见的区域”;
- 舍弃置换重要性——类似于Lei等人提出的保留一个协变量的方法:舍弃特征,再训练模型,比较得分。
- 置换再学习重要性——置换特征,再训练模型,比较得分。
测试
为了了解特征相关性对置换重要性和其他特征重要性方法的影响程度,本文进行了以下实验。
测试方法
首先,生成一个具有指定数量的特性和样本的正态分布数据集(n_features=50,n_samples=10000)。所有特征的平均值为0,标准差为1。所有的数据集特征通过最大相关度(max_correlation)相互关联。
生成数据集后,为每个特征添加了均匀分布的噪声。每个特征的噪声量是从([-0.5noise_magnitude_max,0.5noise_magnitude_max],noise_magnitude_max=var)的均匀分布中随机选择的。这样做是为了降低特征相关性。至此,特征就生成完毕了。
现在我们需要创建一个指标。对于每个特征,生成了一个权重,它是从具有指定gamma和scale参数(gamma=1,scale=1)的gamma分布中采样的。选择Gamma分布是因为它看起来非常类似于典型的特征重要性分布。然后将每个特征权重除以权重之和,使权重之和等于1。这样做是为了减少随机权重生成对最终结果的影响。
然后将指标设置为特征与相应特征权重的线性组合。
对于生成的数据集和目标,本文使用以下参数训练了一个LightGBM模型:
learning_rate: 0.01
n_estimators: 100
random_state: 42
所有其他参数均为默认值。并且使用内置的增益重要性、SHAP重要性和置换重要性算法来计算每个特征的重要性等级(置换重复五次,得分取平均值)。
然后计算特征的重要性与实际重要性之间的Spearman秩相关系数。实际重要性等于秩(-weights)。最佳可能的相关性系数为1.0,即特征重要性与实际重要性(特征权重)的顺序相同。
每个实验的数据(数据集统计相关性,模型重要性与内置增益重要性、SHAP重要性和置换重要性之间的Spearman秩相关系数)被保存以供进一步分析。这个实验用不同的初始值,用不同的最大相关系数和噪声幅值最大值组合(max_correlation,noise_magnitude_max)进行了50次试验。也用“舍弃置换重要度”和“置换再训练重要度”方法进行了同样的实验,但由于需要大量的计算,只进行了5次。
示例分析
为了直观理解,接下来将拿一个实验举例说明。实验的具体代码可以在这里找到:示例实验。实验参数为:
TASK = "classification"
OBJECTIVE = "binary"
METRIC = roc_auc_score
MU = 0
VAR = 1
N_FEATUES = 50
N_SAMPLES = 10_000
NOISE_MAGNITUDE_MAX = 1
SEED = 42
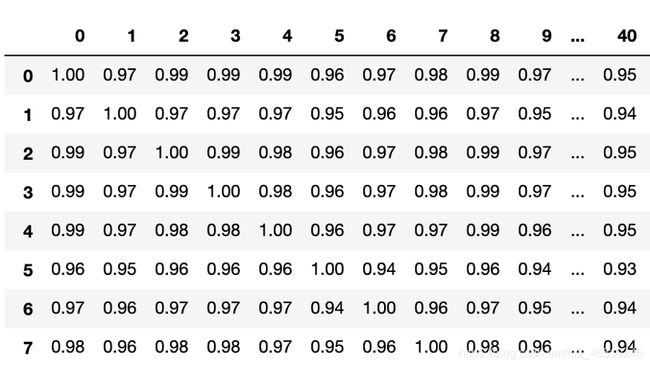
生成数据集的相关矩阵的一部分:
我们可以看到这些特征之间高度相关(平均绝对相关约为0.96)。相关统计:
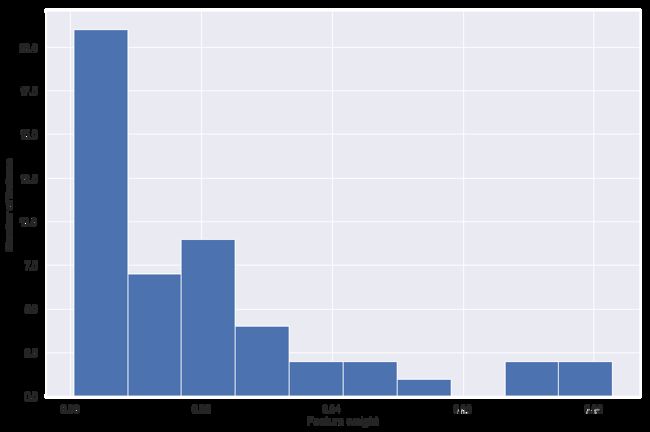
生成特征权重的分布:
计算的特征重要性和实际重要性之间的Spearman rank相关性:
Model's score [train data]: 0.9998
Permutation spearman corr: 0.5724
SHAP spearman corr: 0.4721
LGB gain spearman corr: 0.4567
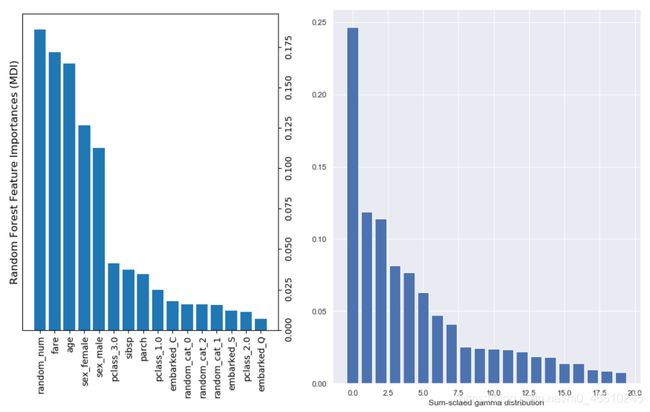
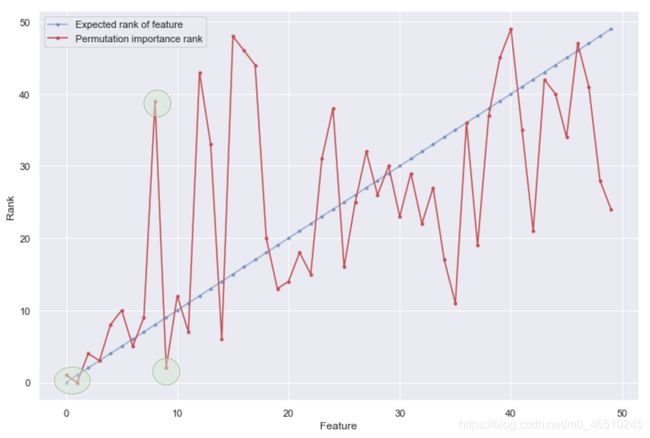
以及实际和计算特征重要性的图示如下:
我们可以在这里看到几个问题(用绿色圆圈标记):
- 最重要和第二重要的特征排序不匹配;
- 根据置换重要性,第三个最重要的特征应该是第九个特征;
- 如果我们相信置换重要性,实际的第8个重要特征下降到第39位。
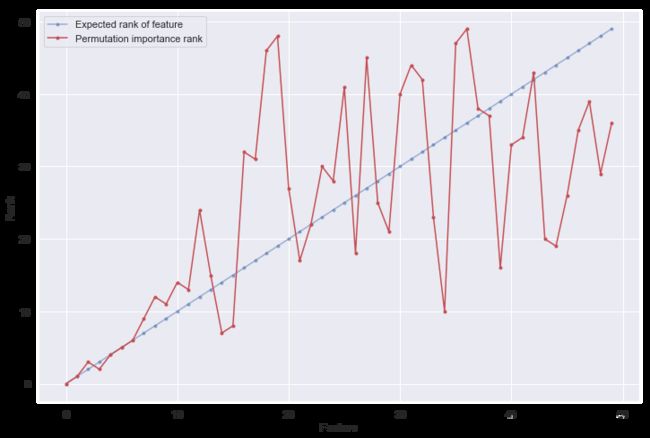
以下是对相同实验参数的实际和计算的特征重要性排序的说明,noise_magnitude_max=10(abs_correlation_mean从0.96下降到0.36):
Model's score [train data]: 0.9663
Permutation spearman corr: 0.6430
SHAP spearman corr: 0.7139
LGB gain spearman corr: 0.6978
仍然不是完美的,但是对于前十位重要特征排序效果良好。
实验结果
本节介绍实验以及对应结果。“permutaions vs SHAP vs Gain”实验总共进行了1200次,而“permutaions vs Relearning”实验则进行了120次。
permutaions vs SHAP vs Gain
在本小节中,将比较使用置换重要性、SHAP值和内置增益计算的特征重要性排序。
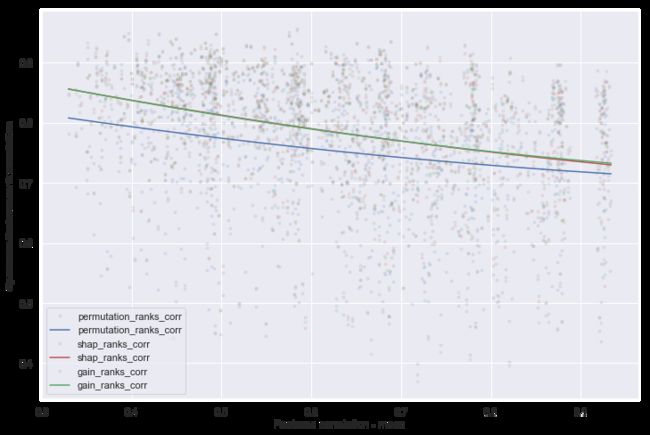
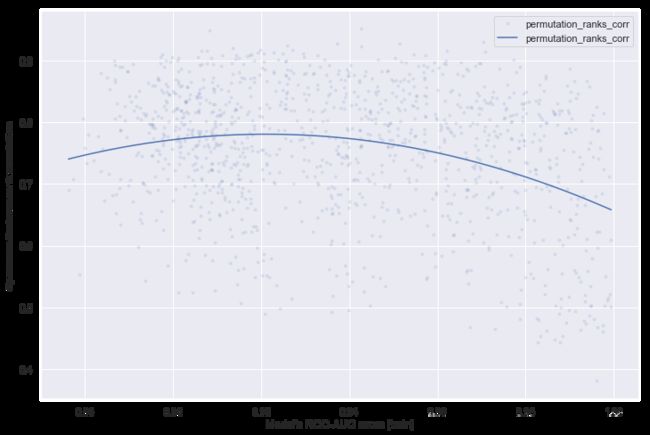
从下面的图中,我们可以看到实际特征重要性与计算特征重要性(置换重要性、SHAP值、内置增益重要性)之间的相关性,正如预期的那样,与特征相关性的平均值和最大值呈负相关。置换重要性受高度相关特征的影响最大。内置增益和SHAP计算的重要性没有区别。
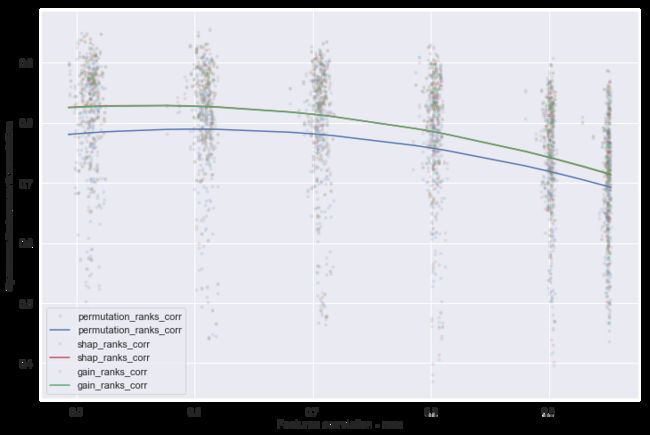
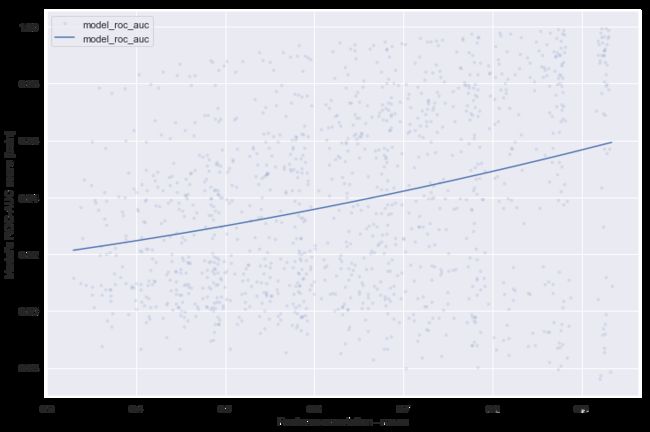
此外,我们可以看到实际特征重要性和计算结果之间的相关性取决于模型的得分:得分越高,相关性越低(图10)。目前还不清楚为什么会发生这种情况,但可以假设,更多的相关特征会导致更精确的模型(从图11中可以看出),因为特征空间更密集,“未知”区域更少。
Permutations vs Relearning
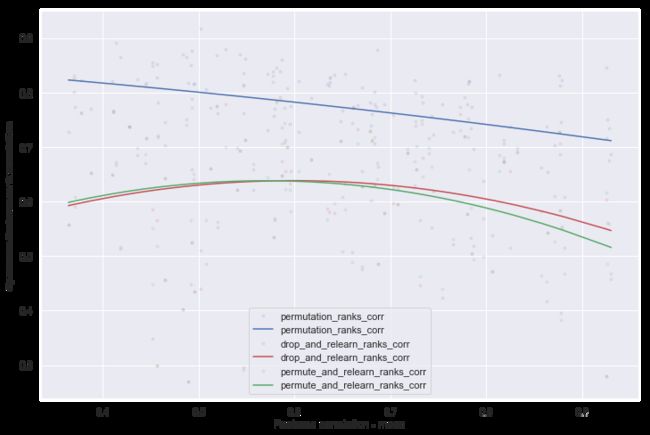
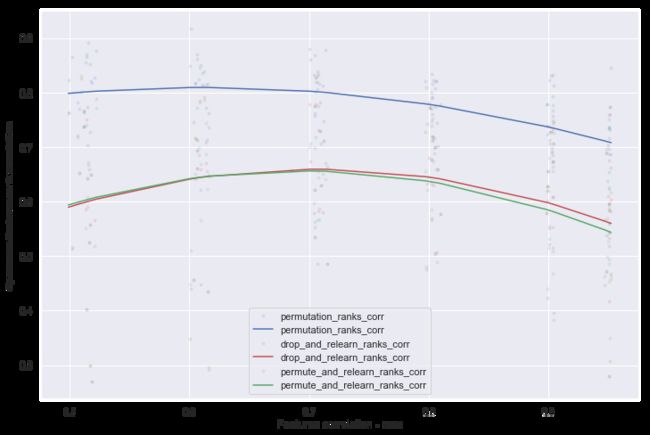
在本小节中,将置换重要性与再学习方法进行比较。
令人惊讶的是,再学习方法在所有相关关系中的表现明显比置换差,这可以从下面的图中看出。另外,再学习方法花费了大约n_features数倍的时间来运行。
结论
- 不要使用置换重要性来解释基于树的模型(或任何在看不见的区域内插得很差的模型)。
- 使用SHAP值或内置的“增益重要性”。
- 不要使用“置换并重新学习”或“删除并重新学习”的方法来查找重要特性。
总结
在这篇文章中,描述了置换重要性方法以及与之相关的问题。展示了高度相关的特征如何以及为什么会影响置换重要性,这将导致误导性的结果。做了一个实验,结果表明置换重要性受高度相关特征的影响最大。还展示了,尽管重新学习方法被认为是有希望的,但是它们的表现比置换的重要性更差,并且需要更多的时间来运行。
这篇文章的主题和实验都是受到了Giles Hooker 和Lucas Mentch.的作品Please Stop Permuting Features An Explanation and Alternatives (https://arxiv.org/abs/1905.03151) 的启发。
作者:Denis Vorotyntsev
本文代码:https://github.com/DenisVorotyntsev/StopPermutingFeatures
deephub翻译组