手写代码实现mini_batch以及神经网络预测波士顿房价（百度飞桨paddle公开课2020/8/12）感谢百度，2333，给个礼物波，muamua

关于波士顿房价数据集的下载与安装

首先说百度的paddle真的可以解放我们双手与大脑，看看我本文中的工作量就清楚了，另外matlab都能禁，万一tf torch也给和谐了，对吧。所以多学个框架对我们也是很有好处的。同时感谢百度免费的公开课，谢谢，谢谢。
回到正文，本文采用keras.datasets中的boston数据集，导入方法如下图所示：

from keras.datasets import boston_housing
(train_x,train_y),(test_x,test_y)=boston_housing.load_data()

但是没有的伙计估计下不了，这里你可以先从网上找到波士顿数据集的文件，然后放置于：C:\Users\你家电脑用户名的名称s\datasets。然后直接运行上方代码，就可以成功运行了。

关于神经网络

神经网络的手动搭建需要用到numpy库进行矩阵运算。
同时补充最关键的数学知识
if y=np.matmul(x,w)+b
dy/dx=np.matmul(dy,w.T)
dy/dw=np.matmul(x.T,dy)
dy/db=dy
关于神经网络的原理就不多说了

关于mini_batch的实现

sklearn库里有skfold函数，挺好用的，这里手写mini_batch主要是为了玩耍。
参数有四个：输入数据集，Label，batch_size，是否正则化，是否洗牌。

def creat_bunch(Input,Label,bunch_size,random_shuffle=False,normalization=False):
   
    if not isinstance(Input,np.ndarray):
        Input=np.array(Input)
    
    if normalization==True:
        MAX=Input.max(axis=1)
        MIN=Input.min(axis=1)
        MEAN=Input.sum(axis=1)/Input.shape[0]
        for i in range(Input.shape[1]):
            Input[:,i]=(Input[:,i]-MEAN)/(MAX-MIN)
        print("normalization ready")
        print("  ")
        
   if random_shuffle==True:
	    EVEN=1
        if Input.shape[0]//2!=0:
            EVEN=0
        if EVEN==1:
            mid=Input.shape[0]/2
            for i in range(int(mid)):
                index_choice=int(np.random.randint(0,mid))
                index2=int(index_choice+mid-1)
                Input[[index_choice,0,index2],:]
                Label[[index_choice,0,index2]]
        else:
            mid=(Input.shape[0]+1)/2
            for i in range(int(mid)-1):
                index_choice=int(np.random.randint(0,mid))
                index2=int(2*(mid-1)-index_choice)
                Input[[index_choice,0,index2],:]
                Label[[index_choice,0,index2]]
        print("shuffle ready")
        print("  ")

    Size=len(Label)
    
    if Size//bunch_size==0:
        Bunch_num=Size/bunch_size
    else:
        Bunch_num=Size//bunch_size+1
    
    Input_bunch=[]
    Label_bunch=[]
    print("total {0} pieces".format(Bunch_num))
    for i in range(Bunch_num):
        print("{0}th bunch is ready!".format(i+1))
        if i!=Bunch_num-1:
            Input_bunch.append(Input[i*bunch_size:(i+1)*bunch_size,:])
            Label_bunch.append(Label[i*bunch_size:(i+1)*bunch_size])
        else:
            Input_bunch.append(Input[(i-1)*bunch_size:Input.shape[0],:])
            Label_bunch.append(Label[(i-1)*bunch_size:Input.shape[0]])
    print("complete!")
    return Input_bunch,Label_bunch

ok，mini_batch实现了。如果直接运行我的有问题的话，可以找找缩进是否存在错误，我写的源代码是没有错的。

房价预测之一层神经网络的实现

由于该数据集不大，所以我没有minibatch处理，直接干拉。
标准化feature

def normoralization(data):
    try:
        MAX=data.max(axis=1)
        MIN=data.min(axis=1)
        MEAN=data.sum(axis=1)/data.shape[0]
        for i in range(data.shape[1]):
            data[:,i]=(data[:,i]-MEAN)/(MAX-MIN)
        return data
    except Exception as result:
        print(result)
train_x=normoralization(train_x)

一层神经网络的实现without激活函数

class network:
    def __init__(self,Input,Label):
        self.weighten=np.random.random((Input.shape[1],1))
        self.bias=np.random.random((Input.shape[0],1))
        self.Input=Input
        self.Label=Label
    def predict(self):
        self.predict_=np.matmul(self.Input,self.weighten)+self.bias
        return self.predict_
    def cost(self):
        error=(self.predict_-self.Label.reshape(-1,1))
        self.error_=error
        for i in range(error.shape[0]):
            error[i]=error[i]*error[i]
        self.error=error
        return np.sum(self.error)/self.error.shape[0]
    def backward(self,leraning_rate):
        for i in range(self.weighten.shape[0]):
            dic=np.mean(self.error_*(-self.Input[:,i]*0.0001)*leraning_rate)
            self.weighten[i]=self.weighten[i]+abs(dic)
        self.bias=self.bias+abs(self.error_*0.0001)

模型训练并且绘制损失函数

import matplotlib.pyplot as plt
%matplotlib inline
net=network(train_x,train_y)
net.predict()
loss=[]
for i in range(5000):
    net.predict()
    net.cost()
    net.backward(0.0000000000001)
    loss.append(net.cost())
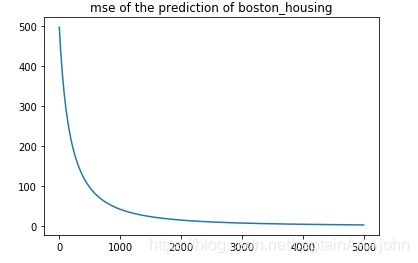
plt.title("mse of the prediction of boston_housing")
plt.plot(loss)
plt.show()

损失函数图像：

最后我简单地实现了一下两层神经网络的实现，基于反向传播

两层神经元简单实现

定义各类函数
relu

class relu():
    def __init__(self):
        pass
    def prediction(self,Input):
        for i in range(Input.shape[0]):
            for j in range(Input.shape[1]):
                Input[i,j]=max(Input[i,j],0)
        return Input
    def backward(self,diff):
        for i in range(diff.shape[0]):
            for j in range(diff.shape[1]):
                if diff[i,j]>0:
                    diff[i,j]=1
                else:
                    diff[i,j]=0
        return diff

matmul

class matmul():
    def __init__(self):
        pass
    def prediction(self,x,w,b):
        result=np.matmul(x,w)+b
        return result
    def backward(slef,diff,x,w,b):
        b_diff=diff
        w_diff=np.matmul(x.T,diff)
        return b_diff,w_diff,np.matmul(diff,w.T)

mse（mean squared error）

class mean_squared_error:
    def __init__(self):
        pass
    def prediction(self,y,label):
        cost=(y-label.reshape(-1,1))
        return cost*cost
    def backward(self,diff,y,label):
        return 2*(y-label.reshape(-1,1))*y

定义参数

#parameters
Epoch=20
Learning_rate=1e-20*3

初始化变量

w1=np.random.random((train_x.shape[1],5))
b1=np.random.random((train_x.shape[0],5))
w2=np.random.random((5,1))
b2=np.random.random((train_x.shape[0],1))

开始训练

mse=mean_squared_error()
matmul=matmul()
activation=relu()

接上

for j in range(100000):
        
        #prediction
        y1=matmul.prediction(train_x,w1,b1)
        y2=activation.prediction(y1)
        y3=matmul.prediction(y2,w2,b2)
        
        #optimize
        cost=mse.prediction(y3,train_y)
        error=np.mean(cost,axis=0)
        
        #backward
        diff=mse.backward(0.00001,cost,train_y)
        b2_diff,w2_diff,diff2=matmul.backward(diff,y2,w2,b2)
        diff3=activation.backward(diff2)
        b1_diff,w1_diff,diff4=matmul.backward(diff3,train_x,w1,b1)
        
        b2-=b2_diff*Learning_rate
        w2-=w2_diff*Learning_rate
        b1-=b1_diff*Learning_rate
        w1-=w1_diff*Learning_rate
        print("the {0} turn's loss is {1}".format(j,error))

完成，请大佬指出不足。也请各位施舍个赞，谢谢各位。比我还要新手的新手，建议不要把时间花在这上面，一方面算法用CPP可能写的更nice一点，另一方面学下paddle吧，可以让你事半功倍。