数据结构-链式二叉树（前序遍历-中序遍历-后续遍历-层序遍历）

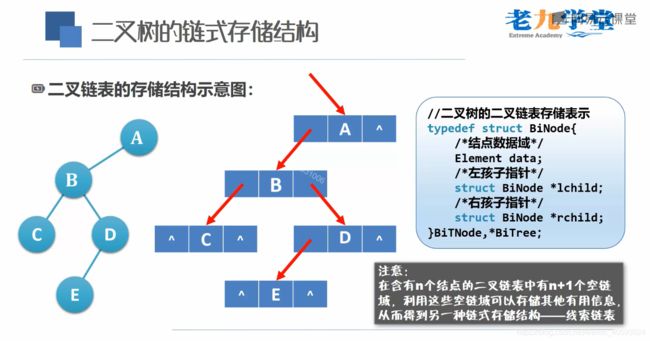
数据结构-链式二叉树

1、前言

2、n遍历

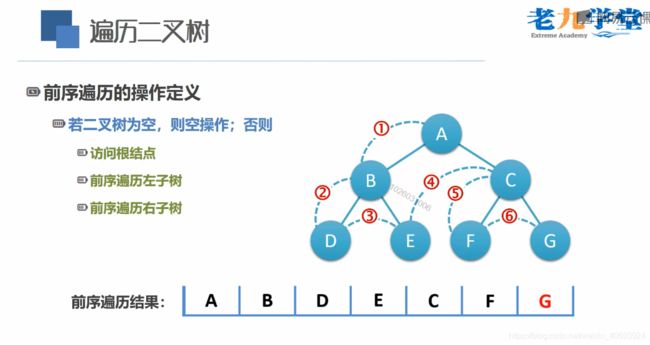
（1）前序遍历

它是树结构插入、删除、修改、查找和排序运算的前提，是二叉树一切运算的基础和核心。

遍历二叉树----从根结点出发，按照某种次序依次访问二叉树中所有结点，使得每个结点均被访问一次且仅被访问一次。

前序遍历的操作意义

心法口诀：根 - 左 - 右

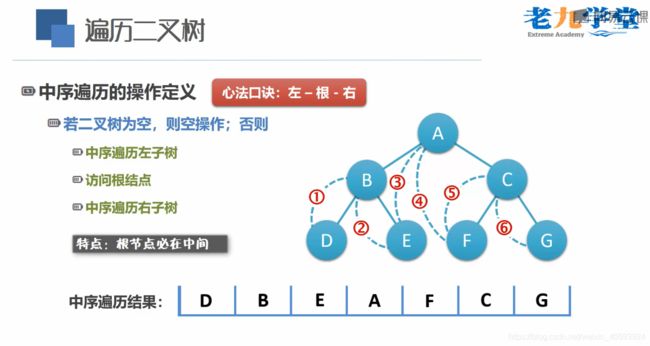
（2）中序遍历

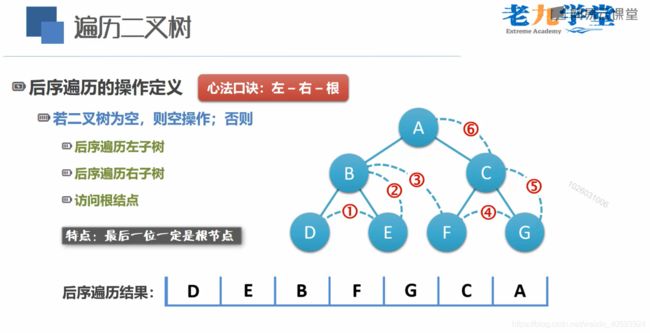
（3）后序遍历

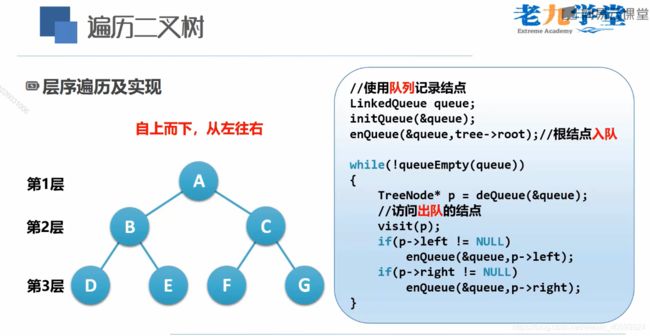
（4）层序遍历

总结

上代码：

#pragma warning(disable:4996)
#include
#include
#include
#include
#include
#include
using namespace std;

#define MAX_SIZE 1024
// 用来实现结点id的自增长
static int id = 0;

// 1、 数据元素
struct ElementType
{
	int id;
	char name[MAX_SIZE];
};

// 2、树结点
struct TreeNode
{
	ElementType data;			// 树结点的数据域
	struct TreeNode* left;		// 左子树
	struct TreeNode* right;		// 右子树
};

/** 3、二叉链表的实现*/
struct BinaryTree
{
	TreeNode* root;			// 二叉链的根结点
	int length;				// 二叉链结点的总数
	int depth;				// 二叉链表的深度
	int diameter;			// 直径-从叶结点到叶结点的最长路径
};


/** 4、初始化空二叉树*/
void InitBinaryTree(BinaryTree* tree);

// 5、创建二叉树(外部需要事先对结点分配内存)
// 返回值为0时，表示创建失败（不创建）
int CreateBinaryTree(TreeNode* root);

// 6、前序遍历：也叫做先根遍历、先序遍历、前序周游。可以记做根 - 左 - 右
void PreOrderTraverse(TreeNode* node);

// 7、模仿用户输入的顺序
char* nodeNames[] = { "A", "B", "D", "#", "#", "E", "#", "#", "C", "F", "#", "#", "G", "#", "#" };
static int nodeNameIndex = 0;
// 8、测试版的创建函数
// 返回值为0时，表示创建失败（不创建）
int CreateBinaryTree_Test(TreeNode* root);

// 9、中序遍历：也叫做中根遍历、中序周游。顺序：左 - 中 - 右 
void InOrderTraverse(TreeNode* node);

// ======================================使用栈实现中序遍历=====================



// 10、为了实现非递归方式的二叉链表遍历，我们自定义一个链栈结构
// 栈结点
struct StackNode
{
	TreeNode* data;			// 数据域 - 与之前实现的链栈有所不同
	StackNode* next;		// 指针域
};


// 11、链栈结构
struct LinkedStack
{
	StackNode* top;				// 栈顶指针
	int length;					// 栈长度
};

// 12、初始化链栈
void InitLinkedStack(LinkedStack* linkedStack);

// 13、入栈
int Push(LinkedStack* linkedStack, TreeNode* node);

// 14、出栈
int Pop(LinkedStack* linkedStack, TreeNode** node);

// 15、// 非递归方式的中序遍历
void InOrderTraverse_Re(TreeNode* node);

// 17、判断栈是否为空
int IsLinkedStackEmpty(LinkedStack* linkedStack);

// 18、后序遍历：也叫做后根遍历、后序周游。 左 - 右 - 根
void PostOrderTraverse(TreeNode* node);

// =======================链队列 - 用于二叉链表的层序遍历===========================
// 19、链队结点
struct QueueNode
{
	TreeNode* data;			// 数据域
	QueueNode* next;			// 指针域
};

// 20、链队列
struct LinkedQueue
{
	QueueNode* qFront;		// 队头指针
	QueueNode* qRear;		// 队尾指针
};

// 21、初始化队列
void InitLinkedQueue(LinkedQueue* linkedQueue);

// 22、入队
void EnQueue(LinkedQueue* linkedQueue, TreeNode* data);

// 23、出队
TreeNode* DeQueue(LinkedQueue* linkedQueue);

// 24、队列是否为空
int IsLinkedQueueEmpty(LinkedQueue* linkedQueue);

// 25、层序遍历：不需要递归，遍历时需要用到队列
void ZOrderTraverse(TreeNode* node);

// ============================测试=====================
void TestBinaryTree()
{
	cout << "=============测试代码=============" << endl;
	BinaryTree tree;
	InitBinaryTree(&tree);
	// 容易遗漏的点：根结点需要事先分配内存
	tree.root = new TreeNode();
	cout << "请输入根结点： ";
	// 下面函数根据用户自己输入创建二叉树
	//CreateBinaryTree(tree.root);
	// 下面函数根据数组创建二叉树
	CreateBinaryTree_Test(tree.root);
	cout << "==============前序遍历结果=============" << endl;
	PreOrderTraverse(tree.root);

	cout << "===============中序遍历结果============" << endl;
	InOrderTraverse(tree.root);

	cout << "=================非递归的中序遍历==============" << endl;
	InOrderTraverse_Re(tree.root);
	
	cout << "==================后序遍历结果======================" << endl;
	PostOrderTraverse(tree.root);

	cout << "===================层序遍历==========================" << endl;
	ZOrderTraverse(tree.root);

	delete(tree.root);


}


int main()
{

	TestBinaryTree();

	system("pause");
}

/** 4、初始化空二叉树*/
void InitBinaryTree(BinaryTree* tree)
{
	tree->root = NULL;
	tree->depth = 0;
	tree->diameter = 0;
	tree->length = 0;
}

// 5、创建二叉树(外部需要事先对结点分配内存)
int CreateBinaryTree(TreeNode* root)
{
	// 根结点如果为空，就退出创建过程
	if (!root) return 0;
	char inputName[MAX_SIZE];		// 用户输入的结点名
	cin >> inputName;
	// 用户输入回车表示结束当前子树的创建
	if (strcmp(inputName, "#") == 0)  return 0;

	// 创建当前结点
	root->data.id = ++id;
	strcpy(root->data.name, inputName);
	// 为输入左右结点做准备-为左右结点指针分配内存
	root -> left = new TreeNode();
	root->right = new TreeNode();
	// 分别递归创建左子树和右子树
	cout << "左结点： ";
	if (CreateBinaryTree(root->left) == 0)
	{
		// 不再创建这个结点则销结点刚分配的内存
		delete(root->left);
		root->left = NULL;
	}
	cout << "右结点： ";
	if (CreateBinaryTree(root->right) == 0)
	{
		delete(root->right);
		root->right = NULL;
	}
	return 1;
}

// 6、前序遍历：也叫做先根遍历、先序遍历、前序周游。可以记做根 - 左 - 右
void PreOrderTraverse(TreeNode* node)
{
	// 先访问根结点，然后遍历左子树，最后遍历右子树
	if (node)
	{
		cout << node->data.id << "    " << node->data.name << endl;
		PreOrderTraverse(node->left);
		PreOrderTraverse(node->right);
	}
}
// 8、测试版的创建函数
// 返回值为0时，表示创建失败（不创建）
int CreateBinaryTree_Test(TreeNode* root)
{
	// 根结点如果为空，就退出创建过程
	if (!root) return 0;
	char inputName[MAX_SIZE];		// 用户输入的结点名
	// cin >> inputName;
	strcpy(inputName, nodeNames[nodeNameIndex++]);
	// 用户输入回车表示结束当前子树的创建
	if (strcmp(inputName, "#") == 0)  return 0;

	// 创建当前结点
	root->data.id = ++id;
	strcpy(root->data.name, inputName);
	// 为输入左右结点做准备-为左右结点指针分配内存
	root->left = new TreeNode();
	root->right = new TreeNode();
	// 分别递归创建左子树和右子树
	//cout << "左结点： ";
	if (CreateBinaryTree_Test(root->left) == 0)
	{
		// 不再创建这个结点则销结点刚分配的内存
		delete(root->left);
		root->left = NULL;
	}
	//cout << "右结点： ";
	if (CreateBinaryTree_Test(root->right) == 0)
	{
		delete(root->right);
		root->right = NULL;
	}
	return 1;
}

// 9、中序遍历：也叫做中根遍历、中序周游。顺序：左 - 中 - 右 
void InOrderTraverse(TreeNode* node)
{
	if (node)
	{
		InOrderTraverse(node->left);
		cout << node->data.id << "    " << node->data.name << endl;
		InOrderTraverse(node->right);
	}
}


// 12、初始化链栈
void InitLinkedStack(LinkedStack* linkedStack)
{
	linkedStack->top = NULL;
	linkedStack->length = 0;
}

// 13、入栈
int Push(LinkedStack* linkedStack, TreeNode* node)
{
	StackNode* tempNode = new StackNode();
	tempNode->data = node;
	tempNode->next = linkedStack->top;
	linkedStack->top = tempNode;
	linkedStack->length++;
	return 1;
}

// 14、出栈
int Pop(LinkedStack* linkedStack, TreeNode** node)
{
	StackNode* tempNode;
	if (linkedStack->top == NULL || linkedStack->length == 0)
	{
		return 0;
	}
	// 返回栈中的数据域 - 理解难点
	*node = linkedStack->top->data;
	tempNode = linkedStack->top;
	linkedStack->top = linkedStack->top->next;
	delete(tempNode);
	linkedStack->length--;
	return 1;
}

// 15、// 非递归方式的中序遍历
void InOrderTraverse_Re(TreeNode* node)
{
	// 思路：
	// 根据中序遍历的顺序，对任意结点来讲，优先访问左孩子，而左孩子又可以看作一个根结点
	// 然后继续访问左孩子结点为空的结点，按照相同的规则访问右子树
	LinkedStack linkedStack;
	InitLinkedStack(&linkedStack);
	TreeNode *root = node;
	// currNode用来保存每个出栈的结点指针
	TreeNode* currNode = new TreeNode();
	// 还需要一个临时指针，用来确保最后释放掉上面分配的内存
	TreeNode* tempNode = currNode;
	while (root || !IsLinkedStackEmpty(&linkedStack))
	{
		if (root)
		{
			Push(&linkedStack, root);
			root = root->left;
		}
		else
		{
			// 难点
			Pop(&linkedStack, &currNode);
			cout << currNode->data.id << "    " << currNode->data.name << endl;
			root = currNode->right;
		}
	}

	delete(tempNode);
}

// 17、判断栈是否为空
int IsLinkedStackEmpty(LinkedStack* linkedStack)
{
	if (linkedStack->top == NULL || linkedStack->length == 0)
	{
		return 1;
	}
	return 0;
}

// 18、后序遍历：也叫做后根遍历、后序周游。 左 - 右 - 根
void PostOrderTraverse(TreeNode* node)
{
	if (node)
	{
		PostOrderTraverse(node->left);
		PostOrderTraverse(node->right);
		cout << node->data.id << "    " << node->data.name << endl;
	}
}


// 21、初始化队列
void InitLinkedQueue(LinkedQueue* linkedQueue)
{
	linkedQueue->qFront = new QueueNode();
	linkedQueue->qFront->next = NULL;
	linkedQueue->qRear = linkedQueue->qFront;
}

// 22、入队
void EnQueue(LinkedQueue* linkedQueue, TreeNode* data)
{
	QueueNode* node = new QueueNode();
	node->data = data;
	node->next = NULL;
	linkedQueue->qRear->next = node;
	linkedQueue->qRear = node;
}

// 23、出队
TreeNode* DeQueue(LinkedQueue* linkedQueue)
{
	TreeNode* data = NULL;			// 用来返回
	if (linkedQueue->qFront == linkedQueue->qRear) return data;
	QueueNode* node = linkedQueue->qFront->next;
	data = node->data;
	linkedQueue->qFront->next = node->next;
	if (linkedQueue->qRear == node)
	{
		linkedQueue->qRear = linkedQueue->qFront;
	}
	delete(node);

	return data;
}

// 24、队列是否为空
int IsLinkedQueueEmpty(LinkedQueue* linkedQueue)
{
	if (linkedQueue->qFront == linkedQueue->qRear)
	{
		return 1;
	}
	return 0;
}

// 25、层序遍历：不需要递归，遍历时需要用到队列
void ZOrderTraverse(TreeNode* node)
{
	LinkedQueue queue;
	InitLinkedQueue(&queue);
	// 根结点入队
	EnQueue(&queue, node);
	while (!IsLinkedQueueEmpty(&queue))
	{
		TreeNode* node = DeQueue(&queue);
		cout << node->data.id << "    " << node->data.name << endl;
		if (node->left != NULL)
		{
			EnQueue(&queue, node->left);
		}
		if (node->right != NULL)
		{
			EnQueue(&queue, node->right);
		}
	}
}