SLAM算法评估中的轨迹拟合与外参求解
文章同步更新到github pages,欢迎收藏
文章目录
- 问题描述
- 数学关系
- 求解方法
- 求解$_{gp}^{gv}T$
- 求解$_{lp}^{lv}T$
- 交替迭代优化
- 时间戳对齐
- 实验结果
- 参考文献
问题描述
SLAM中常常碰到对齐(align)两个不同设备采集的轨迹的问题。比如通过VICON跟踪获得了一组轨迹,手机通过SLAM算法也获得一组轨迹,要评估SLAM算法的精度,就需要将手机获得的轨迹与作为真值的VICON轨迹对齐。
数学关系
设 l p g p T _{lp}^{gp}T lpgpT代表手机(phone)从当前局部坐标系(local)到SLAM算法定义的世界坐标系(global)的变换,即当前手机在SLAM算法定义的世界坐标系下的位姿。
设 l v g v T _{lv}^{gv}T lvgvT代表从VICON的当前刚体坐标系到VICON定义的世界坐标系的变换,即VICON跟踪的刚体在VICON世界坐标系下的位姿。
设 g p g v T _{gp}^{gv}T gpgvT代表两个世界坐标系之间的变换
设 l p l v T _{lp}^{lv}T lplvT代表当前刚体坐标系与手机坐标系之间的变换
这几个变换满足:
g p g v T ∗ l p g p T = l v g v T ∗ l p l v T _{gp}^{gv}T\ *\ _{lp}^{gp}T\ =\ _{lv}^{gv}T\ *\ _{lp}^{lv}T gpgvT ∗ lpgpT = lvgvT ∗ lplvT
其中 l p g p T _{lp}^{gp}T lpgpT和 l v g v T _{lv}^{gv}T lvgvT均是已知量,多个 l p g p T _{lp}^{gp}T lpgpT和 l v g v T _{lv}^{gv}T lvgvT各自构成了两条运动轨迹,轨迹中的每一帧记为 l p g p T i _{lp}^{gp}T_i lpgpTi和 l v g v T j _{lv}^{gv}T_j lvgvTj。 g p g v T _{gp}^{gv}T gpgvT和 l p l v T _{lp}^{lv}T lplvT是待求解的未知量。如果手机与VICON刚体是刚性连接的,在整个运动过程中, g p g v T _{gp}^{gv}T gpgvT和 l p l v T _{lp}^{lv}T lplvT的值是定值。
求解方法
优化的目标函数为:
min g p g v T , l p l v T ∑ i ∥ g p g v T ∗ l p g p T i − l v g v T j ( i ) ∗ l p l v T ∥ F 2 \min_{_{gp}^{gv}T,\ _{lp}^{lv}T} \sum_{i}\Vert\ _{gp}^{gv}T\ *\ _{lp}^{gp}T_i\ -\ _{lv}^{gv}T_{j(i)}\ *\ _{lp}^{lv}T\ \Vert_F^2 gpgvT, lplvTmini∑∥ gpgvT ∗ lpgpTi − lvgvTj(i) ∗ lplvT ∥F2
其中 l v g v T j ( i ) _{lv}^{gv}T_{j(i)} lvgvTj(i)表示在时间戳上与 l p g p T i _{lp}^{gp}T_i lpgpTi对应的某一帧。
上式不好直接优化,原因在于
- 自由度过大,如果旋转用四元数表示,上式要同时优化12个自由量。
- 约束不足,存在奇异解,比如 g p g v T _{gp}^{gv}T gpgvT和 l p l v T _{lp}^{lv}T lplvT均为零,显然是上式的一个极小解。
因此考虑分部优化。
求解 g p g v T _{gp}^{gv}T gpgvT
首先假定 l p l v T _{lp}^{lv}T lplvT已知,只求解 g p g v T _{gp}^{gv}T gpgvT,相当于是寻找一个刚体变换将已知轨迹 l p g p T _{lp}^{gp}T lpgpT变换为另一个已知轨迹 l v g v T ∗ l p l v T _{lv}^{gv}T\ *\ _{lp}^{lv}T lvgvT ∗ lplvT,并满足最小二乘。这类问题有一个高效的线性解法。
设 l v g v T ∗ l p l v T = l p g p T _{lv}^{gv}T\ *\ _{lp}^{lv}T\ =\ _{lp}^{gp}T lvgvT ∗ lplvT = lpgpT,两条轨迹的translation部分分别为 l p g p t _{lp}^{gp}t lpgpt和 l p g v t _{lp}^{gv}t lpgvt,将轨迹中的所有translation求均值得到质心 l p g p t ˉ _{lp}^{gp}\bar{t} lpgptˉ和 l p g v t ˉ _{lp}^{gv}\bar{t} lpgvtˉ,然后减去质心,得到中心化后的轨迹
Δ l p g p t i = l p g p t i − l p g p t ˉ Δ l p g v t j = l p g v t j − l p g v t ˉ \begin{aligned} \Delta_{lp}^{gp}t_i&=\ _{lp}^{gp}t_i -\ _{lp}^{gp}\bar{t} \\ \Delta_{lp}^{gv}t_j&=\ _{lp}^{gv}t_j -\ _{lp}^{gv}\bar{t} \end{aligned} ΔlpgptiΔlpgvtj= lpgpti− lpgptˉ= lpgvtj− lpgvtˉ
之后计算两条中心化轨迹中所有translation的协方差矩阵,即
S = 1 n ∑ i n Δ l p g p t i ∗ Δ l p g v t j ( i ) T S=\frac{1}{n}\sum_i^n\Delta_{lp}^{gp}t_i\ *\ \Delta_{lp}^{gv}t_{j(i)}^T S=n1i∑nΔlpgpti ∗ Δlpgvtj(i)T
对协方差矩阵做奇异值分解:
S = U Σ V T S=U\Sigma V^T S=UΣVT
则两条轨迹之间的旋转和位移分别为(证明见参考文献[1]):
g p g v R = V U T g p g v t = l p g v t ˉ − g p g v R ∗ l p g p t ˉ \begin{aligned} _{gp}^{gv}R &= VU^T \\ _{gp}^{gv}t &=\ _{lp}^{gv}\bar{t} - ~_{gp}^{gv}R\ *\ _{lp}^{gp}\bar{t} \end{aligned} gpgvRgpgvt=VUT= lpgvtˉ− gpgvR ∗ lpgptˉ
若 d e t ( V U T ) = − 1 det(VU^T)=-1 det(VUT)=−1,将 V V V的最后一列乘以 − 1 -1 −1后再用上式计算 g p g v R _{gp}^{gv}R gpgvR。
求解 l p l v T _{lp}^{lv}T lplvT
通过上面的方法求出 g p g v T _{gp}^{gv}T gpgvT,将其带回等式,并作为已知量固定,再来单独求解 l p l v T _{lp}^{lv}T lplvT。 l p l v T _{lp}^{lv}T lplvT是右乘量,不能描述为刚体变换。这里提供三种求解方法。
第一种方法,使用数值优化,目标函数与约束如下:
min l p l v T ∑ i ∥ g p g v T ∗ l p g p T i − l v g v T j ( i ) ∗ l p l v T ∥ F 2 s . t . ∥ l p l v q ∥ = 1 \begin{aligned} &\min_{_{lp}^{lv}T} \sum_{i}\Vert\ _{gp}^{gv}T\ *\ _{lp}^{gp}T_i\ -\ _{lv}^{gv}T_{j(i)}\ *\ _{lp}^{lv}T\ \Vert_F^2 \\ &s.t.\ \ \ \ \Vert\ _{lp}^{lv}q\ \Vert = 1 \end{aligned} lplvTmini∑∥ gpgvT ∗ lpgpTi − lvgvTj(i) ∗ lplvT ∥F2s.t. ∥ lplvq ∥=1
其中, l p l v T _{lp}^{lv}T lplvT中的旋转量使用四元数表示,并要求四元数的模长为1。 将约束项作为惩罚项合并到目标函数中,可以得到无约束的非线性优化问题:
min l p l v T ∑ i ∥ g p g v T ∗ l p g p T i − l v g v T j ( i ) ∗ l p l v T ∥ F 2 + w ( ∥ l p l v q ∥ − 1 ) 2 \min_{_{lp}^{lv}T} \sum_{i}\Vert\ _{gp}^{gv}T\ *\ _{lp}^{gp}T_i\ -\ _{lv}^{gv}T_{j(i)}\ *\ _{lp}^{lv}T\ \Vert_F^2 + w( \Vert\ _{lp}^{lv}q\ \Vert - 1)^2 lplvTmini∑∥ gpgvT ∗ lpgpTi − lvgvTj(i) ∗ lplvT ∥F2+w(∥ lplvq ∥−1)2
我们目前将 w w w设为了轨迹中帧的数目。
第二种方法,可以推导出一种线性解法。设已知量 g p g v T ∗ l p g p T i = l p g v T i _{gp}^{gv}T\ *\ _{lp}^{gp}T_i\ =\ _{lp}^{gv}T_i gpgvT ∗ lpgpTi = lpgvTi,并将所有的变换矩阵 T T T表示为旋转矩阵 R R R和位移矢量 t t t,由
l p g v T i = l v g v T j ( i ) ∗ l p l v T _{lp}^{gv}T_i\ =\ _{lv}^{gv}T_{j(i)}\ *\ _{lp}^{lv}T lpgvTi = lvgvTj(i) ∗ lplvT
可得
l p l v R = l v g v R j ( i ) T ∗ l p g v R i l p l v t = l v g v R j ( i ) T ∗ ( l p g v t i − l v g v t j ( i ) ) \begin{aligned} _{lp}^{lv}R\ &=\ _{lv}^{gv}R^T_{j(i)}\ *\ _{lp}^{gv}R_i \\ _{lp}^{lv}t\ &=\ _{lv}^{gv}R^T_{j(i)}\ *\ (\ _{lp}^{gv}t_i\ -\ _{lv}^{gv}t_{j(i)}\ ) \end{aligned} lplvR lplvt = lvgvRj(i)T ∗ lpgvRi= lvgvRj(i)T ∗ ( lpgvti − lvgvtj(i) )
其中,每一对 l p g v T i _{lp}^{gv}T_i lpgvTi和 l v g v T j ( i ) _{lv}^{gv}T_{j(i)} lvgvTj(i)均能求出一组 l p l v R _{lp}^{lv}R lplvR和 l p l v t _{lp}^{lv}t lplvt。最终的位移矢量 l p l v t _{lp}^{lv}t lplvt只需对所有通过上式求得的矢量取平均即可。但是,旋转量由于分布在流形上,要用特殊的方式进行平均。
首先设上式求得的每一个旋转量为 l p l v R i _{lp}^{lv}R_i lplvRi,将他们全部转换为四元数 l p l v q i _{lp}^{lv}q_i lplvqi,将四元数视为4x1的矢量,构成如下4xN矩阵:
Q = [ l p l v q 1 , l p l v q 2 , . . . , l p l v q n ] Q=[\ _{lp}^{lv}q_1,\ _{lp}^{lv}q_2,\ ...,\ _{lp}^{lv}q_n\ ] Q=[ lplvq1, lplvq2, ..., lplvqn ]
然后对4x4矩阵 Q ∗ Q T Q*Q^T Q∗QT求特征值和特征向量,平均后的旋转量 l p l v q _{lp}^{lv}q lplvq即为最大特征值对应的特征向量(证明见参考文献[2])
第三种方法,将其也转换为刚体变换问题。设已知量 g p g v T ∗ l p g p T i = l p g v T i _{gp}^{gv}T\ *\ _{lp}^{gp}T_i\ =\ _{lp}^{gv}T_i gpgvT ∗ lpgpTi = lpgvTi,则将原问题中的变换矩阵都求逆后,可得到如下优化问题:
min l v l p T ∑ i ∥ g v l p T i − l v l p T ∗ g v l v T j ( i ) ∥ F 2 \min_{_{lv}^{lp}T} \sum_{i}\Vert\ _{gv}^{lp}T_i\ -\ _{lv}^{lp}T * \ _{gv}^{lv}T_{j(i)}\ \Vert_F^2 lvlpTmini∑∥ gvlpTi − lvlpT∗ gvlvTj(i) ∥F2
然后使用求解 g p g v T _{gp}^{gv}T gpgvT的方法求出 l v l p T _{lv}^{lp}T lvlpT,最终有 l p l v T = l v l p T − 1 _{lp}^{lv}T~=~_{lv}^{lp}T^{-1} lplvT = lvlpT−1。
三种方法在相同的输入与停止条件下,得到的结果基本上是一致的,只存在较小差异。某些输入下,某种方法要略好于其他,而另一种输入下,又可能略逊与其他。
交替迭代优化
求解出 l p l v T _{lp}^{lv}T lplvT后,又可以带回原等式,作为已知量,然后再次求解 g p g v T _{gp}^{gv}T gpgvT。即不断进行上文的两个求解过程,交替优化 g p g v T _{gp}^{gv}T gpgvT和 l p l v T _{lp}^{lv}T lplvT,直到两个轨迹的绝对误差不再缩小或小于某个阈值。
这个迭代的开始需要给 l p l v T _{lp}^{lv}T lplvT一个初值,由于VICON刚体与手机Body之间的位置差异不大,因此以单位变换作为初值即可。
时间戳对齐
以上算法求解的关键在于找到两个轨迹的对应帧 l p g v T i _{lp}^{gv}T_i lpgvTi和 l v g v T j ( i ) _{lv}^{gv}T_{j(i)} lvgvTj(i),如果两个设备采集时的时间戳是完全同步的,即 j ( i ) = i j(i)=i j(i)=i,则直接根据时间戳找对应关系即可。但是,实际上大多数设备在时间同步后,任然会有不同长度的时间差,少则几毫秒,多则几秒。为了解决这个问题,在执行上文算法前需要对两个轨迹数据估计时间差,并对齐时间戳。
时间戳和轨迹是离散记录的,无法直接使用优化方法得出时间差。常用方法为将轨迹通过样条插值变为连续曲线,这样就得到了时间和位姿的近似连续量,然后使用非线性优化的方式求时间差,详细可见参考文献[3]。
我们使用了一种搜索算法,实现更简单,计算效率更高,但精度稍低(毫秒级精度)。
首先假设两个轨迹的时间差在 ± 10 \pm 10 ±10秒以内,以某条轨迹作为reference(一般选帧率较高的一个,比如VICON),改变另外一条轨迹的时间戳,减10秒,减9秒,直到加9秒,加10秒,步长为1秒。这样就得到20条修改时间戳后的轨迹,每一条轨迹都和reference通过时间戳找对应帧(时间戳相差最小的帧),然后使用求解 g p g v T _{gp}^{gv}T gpgvT的算法拟合两条轨迹,并计算绝对误差(只考虑帧之间的位置,不考虑姿态),取误差最小的轨迹对应的时间差,比如说 − 5 -5 −5秒。然后在 − 5 ± 0.1 -5\pm 0.1 −5±0.1秒的区间内以 0.1 0.1 0.1秒的步长再次做上述操作。直到以 0.001 0.001 0.001秒作为步长搜索后结束。本质上是一种分层次搜索算法。为了提高搜索精度,还可以在使绝对误差最小的时间差附近拟合一条二次曲线(自变量是时间差,因变量是绝对误差),取二次曲线的最小值处的时间差作为最终结果。
实验结果
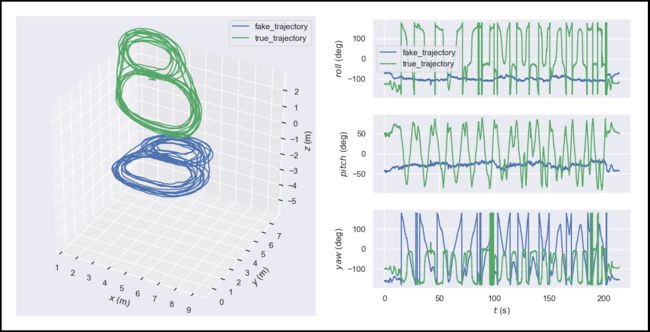
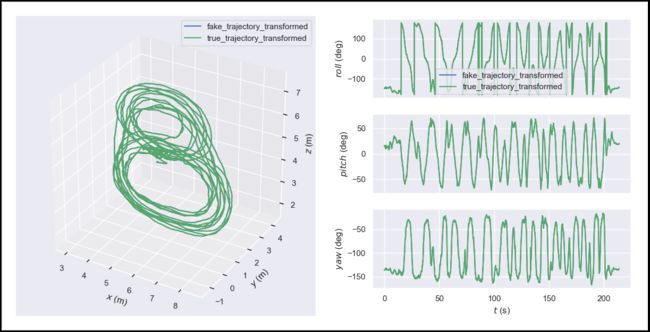
使用一条VICON轨迹(true_trajectory)人为添加外参变换和刚体变换后得到另外一条轨迹(fake_trajectory),同时也人为的加入噪声(0.1度的角度随机偏差,1cm的位置随机偏差)、时间差(与原轨迹相差5.421秒),并降采样(帧率为原轨迹的四分之一)。
参考文献
- Least-Squares Rigid Motion Using SVD
- Quaternion Averaging
- Unified Temporal and Spatial Calibration for Multi-Sensor Systems