神经网络训练与注意点

1 训练

在前面当中我们讨论了神经网络静态的部分：包括神经网络结构、神经元类型、数据部分、损失函数部分等。

这个部分我们集中讲讲动态的部分，主要是训练的事情，集中在实际工程实践训练过程中要注意的一些点，如何找到最合适的参数。

1.1 关于梯度检验

之前的博文我们提到过，我们需要比对数值梯度和解析法求得的梯度，实际工程中这个过程非常容易出错，下面提一些小技巧和注意点：

使用中心化公式，这一点我们之前也说过，使用如下的数值梯度计算公式：

$\frac{d f(x)}{d x}=\frac{f(x+h)-f(x-h)}{2 h}$(好的形式)

而不是

$\frac{d f(x)}{d x}=\frac{f(x+h)-f(x)}{h}$(非中心化形式，不要用)

即使看似上面的形式有着2倍的计算量，但是如果你有兴趣用把公式中的\(f(x+h)\)和\(f(x-h)\)做泰勒展开的话，你会发现上面公式出错率大概是\(O\left(h^{2}\right)\)级别的，而下面公式则是\(O(h)\)，注意到\(h\)是很小的数，因此显然上面的公式要精准得多。

使用相对误差做比较，这是实际工程中需要提到的另外一点，在我们得到数值梯度\(f_{n}^{\prime}\)和解析梯度\(f_{a}^{\prime}\)之后，我们如何去比较两者？第一反应是作差\(\left|f_{a}^{\prime}-f_{n}^{\prime}\right|\)，或者求平方。

但是用绝对值是不可靠的，假如两个梯度的绝对值都在1.0左右，那么我们可以认为1e-4这样一个差值是非常小的，但是如果两个梯度本身就是1e-4级别的，那这个差值就相当大了。所以我们考虑相对误差：

$\frac{\left|f_{a}^{\prime}-f_{n}^{\prime}\right|}{\max \left(\left|f_{a}^{\prime}\right|,\left|f_{n}^{\prime}\right|\right)}$

加max项的原因很简单：整体形式变得简单和对称。但也别忘了避开分母中两项都为0的情况。对于相对误差而言：

• 相对误差>\(1 e-2\)，意味着你的实现肯定是有问题的
• \(1 e-2\)>相对误差>\(1 e-4\)，你会有点担心
• \(1 e-4\)>相对误差，基本是OK的，但是要注意极端情况(使用tanh或者softmax时候出现kinks)那还是太大
• \(1 e-7\)>相对误差，放心大胆使用

随着神经网络层数增多，相对误差是会增大的。这意味着，对于10层的神经网络，其实相对误差也许在1e-2级别就已经是可以正常使用的了。

使用双精度浮点数。如果你使用单精度浮点数计算，那你的实现可能一点问题都没有，但是相对误差却很大。实际工程中出现过，从单精度切到双精度，相对误差立马从1e-2降到1e-8的情况。

要留意浮点数的范围。一篇很好的文章是"What Every Computer Scientist Should Know About Floating-Point Arithmetic"。我们得保证计算时，所有的数都在浮点数的可计算范围内，太小的值(比如h)会带来计算上的问题。

目标函数的不可导点（Kinks）。它指的是一种会导致数值梯度和解析梯度不一致的情况。

会出现在使用ReLU或者类似的神经单元上时，对于很小的负数，比如\(x=-1 e-6\)，因为\(x<0\)，所以解析梯度是绝对为0的，但是对于数值梯度而言，加入你计算\(f(x+h)\)，取的\(h>1 e-6\)，那就跳到大于0的部分了，这样数值梯度就一定和解析梯度不一样了。

而且这个并不是极端情况，对于一个像CIFAR-10这样级别的数据集，因为有50000个样本，同时每个样本会对应9个错误的类别(给损失函数贡献9个loss值)，会有450000个\(\max (0, x)\)，会出现很多的kinks。

注意：在计算损失的过程中是可以知道不可导点有没有被越过的。

在具有\(\max (x, y)\)形式的函数中持续跟踪所有“赢家”的身份，就可以实现这一点。其实就是看在前向传播时，到底x和y谁更大。

如果在计算\(f(x+h)\)和\(f(x-h)\)的时候，至少有一个“赢家”的身份变了，那就说明不可导点被越过了，数值梯度会不准确。。

设定步长h要小心。h肯定不能特别大，这个大家都知道。但并不是说h要设定的非常小，其实h设定的非常小也会有问题，因为h太小可能会有数值精度问题。

很有意思的是，有时候在实际情况中h如果从非常小调为\(1e-4\)或者\(1e-6\)反倒会突然计算变得正常。

不要让正则化项盖过数据项。有时候会出现这个问题，因为损失函数是数据损失部分与正则化部分的求和。

因此要特别注意正则化部分，你可以想象下，如果它盖过了数据部分，那么主要的梯度来源于正则化项，那这样根本就做不到正常的梯度回传和参数迭代更新。

所以即使在检查数据部分的实现是否正确，也得先关闭正则化部分(系数\(\lambda\)设为0)，再检查。

注意dropout和其他参数。在检查数值梯度和解析梯度的时候，如果不把dropout和其他参数都『关掉』的话，两者之间是一定会有很大差值的。

不过『关掉』它们的负面影响是，没有办法检查这些部分的梯度是否正确。

因此，一个更好的解决方案就是在计算\(f(x+h)\)和\(f(x-h)\)前强制增加一个特定的随机种子，在计算解析梯度时也同样如此。

检查少量的维度。在实际中，梯度可以有上百万的参数，在这种情况下只能检查其中一些维度然后假设其他维度是正确的。要小心一点：要保证这些维度的每个参数都检查对比过了。

1.2 训练前的检查工作

在开始训练之前，我们还得做一些检查，来确保不会运行了好一阵子，才发现计算代价这么大的训练其实并不正确。

在初始化之后看一眼loss。其实我们在用很小的随机数初始化神经网络后，第一遍计算loss可以做一次检查数据损失(当然要记得把正则化系数设为0)。

以CIFAR-10为例，如果使用Softmax分类器，我们预测应该可以拿到值为2.302左右的初始loss(因为10个类别，初始概率应该都为0.1，Softmax损失是-ln正确类别的概率):-ln(0.1)=2.302)。

加回正则项，接着我们把正则化系数设为正常的小值，加回正则化项，这时候再算损失loss，应该比刚才要大一些。

试着去拟合一个小的数据集。最后一步，也是很重要的一步，在对大数据集做训练之前，我们可以先训练一个小的数据集(比如20张图片)，然后确保你的神经网络能够做到0损失loss(当然，是指的正则化系数为0的情况下)，因为如果神经网络实现是正确的，在无正则化项的情况下，完全能够过拟合这一小部分的数据。

1.3 训练过程中的监控

开始训练之后，我们可以通过监控一些指标来了解训练的状态。

这些数值输出的图表是观察训练进程的一扇窗口，是直观理解不同的超参数设置效果的工具，从而知道如何修改超参数以获得更高效的学习过程。

1.3.1 损失/loss随每轮完整迭代后的变化

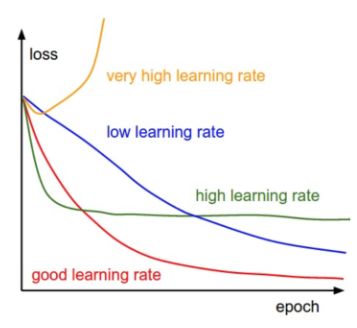
下面这幅图表明了不同的学习率下，我们每轮完整迭代(这里的一轮完整迭代指的是所有的样本都被过了一遍，因为随机梯度下降中batch size的大小设定可能不同，因此我们不选每次mini-batch迭代为周期)过后的loss应该呈现的变化状况：

合适的学习率可以保证每轮完整训练之后，loss都减小，且能在一段时间后降到一个较小的程度。

太小的学习率下loss减小的速度很慢，如果太激进，设置太高的学习率，开始的loss减小速度非常可观，可是到了某个程度之后就不再下降了，在离最低点一段距离的地方反复，无法下降了。

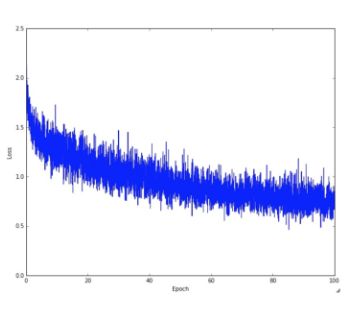
下图是实际训练CIFAR-10的时候，loss的变化情况：

大家可能会注意到上图的曲线有一些上下跳动，不稳定，这和随机梯度下降时候设定的batch size有关系。batch size非常小的情况下，会出现很大程度的不稳定，如果batch size设定大一些，会相对稳定一点。

1.3.2 训练集/验证集上的准确度

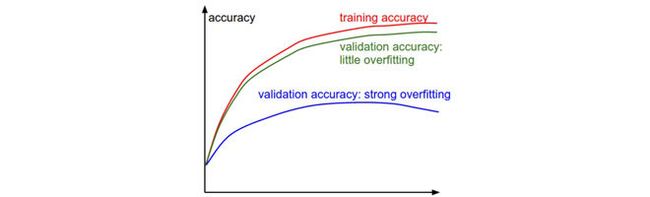
然后我们需要跟踪一下训练集和验证集上的准确度状况，以判断分类器所处的状态(过拟合程度如何)：

随着时间推进，训练集和验证集上的准确度都会上升，如果训练集上的准确度到达一定程度后，两者之间的差值比较大，那就要注意一下，可能是过拟合现象，如果差值不大，那说明模型状况良好。

1.3.3 权重：权重更新部分 的比例

最后一个需要留意的量是权重更新幅度和当前权重幅度的比值。

注意是权重更新部分，不一定是计算出来的梯度。(比如训练用的vanilla sgd，那这个值就是梯度和学习率的乘积)。

最好对于每组参数都独立地检查这个比例。

我们没法下定论，但是在之前的工程实践中，一个合适的比例大概是1e-3。如果你得到的比例比这个值小很多，那么说明学习率设定太低了，反之则是设定太高了。

1.3.4 每一层的 激励/梯度值 分布

如果参数初始化不正确，那整个训练过程会越来越慢，甚至直接停掉。

不过我们可以很容易发现这个问题。表现最明显的数据是每一层的激励和梯度的方差(波动状况)。

举个例子说，如果初始化不正确，很有可能从前到后逐层的激励(激励函数的输入部分)方差变化是如下的状况：

# 我们用标准差为0.01均值为0的高斯分布值来初始化权重(这不合理)
Layer 0: Variance: 1.005315e+00
Layer 1: Variance: 3.123429e-04
Layer 2: Variance: 1.159213e-06
Layer 3: Variance: 5.467721e-10
Layer 4: Variance: 2.757210e-13
Layer 5: Variance: 3.316570e-16
Layer 6: Variance: 3.123025e-19
Layer 7: Variance: 6.199031e-22
Layer 8: Variance: 6.623673e-25

大家看一眼上述的数值，就会发现，从前往后，激励值波动逐层降得非常厉害，这也就意味着反向算法中，计算回传梯度的时候，梯度都要接近0了，因此参数的迭代更新几乎就要衰减没了，显然不太靠谱。

我们按照上一讲中提到的方式正确初始化权重，再逐层看激励/梯度值的方差，会发现它们的方差衰减没那么厉害，近似在一个级别：

# 重新正确设定权重:
Layer 0: Variance: 1.002860e+00
Layer 1: Variance: 7.015103e-01
Layer 2: Variance: 6.048625e-01
Layer 3: Variance: 8.517882e-01
Layer 4: Variance: 6.362898e-01
Layer 5: Variance: 4.329555e-01
Layer 6: Variance: 3.539950e-01
Layer 7: Variance: 3.809120e-01
Layer 8: Variance: 2.497737e-01

再看逐层的激励波动情况，你会发现即使到最后一层，网络也还是『活跃』的，意味着反向传播中回传的梯度值也是够的，神经网络是一个积极learning的状态。

1.3.5 首层的可视化

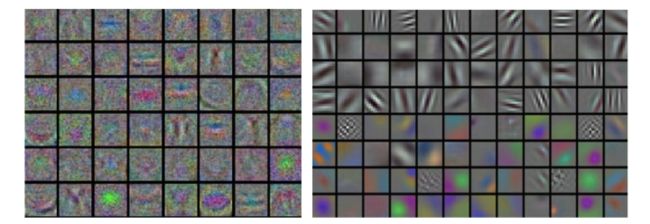
最后再提一句，如果神经网络是用在图像相关的问题上，那么把首层的特征和数据画出来(可视化)可以帮助我们了解训练是否正常：

上图的左右是一个正常和不正常情况下首层特征的可视化对比。

左边的图中特征噪点较多，图像很『浑浊』，预示着可能训练处于『病态』过程：也许是学习率设定不正常，或者正则化系数设定太低了，或者是别的原因，可能神经网络不会收敛。

右边的图中，特征很平滑和干净，同时相互间的区分度较大，这表明训练过程比较正常。

1.4 关于参数更新部分的注意点

当我们确信解析梯度实现正确后，那就该在后向传播算法中使用它更新权重参数了。就单参数更新这个部分，也是有讲究的！

说起来，神经网络的最优化这个子话题在深度学习研究领域还真是很热。下面提一下大神们的论文中提到的方法，很多在实际应用中还真是很有效也很常用。

1.4.1 随机梯度下降与参数更新

vanilla update

这是最简单的参数更新方式，拿到梯度之后，乘以设定的学习率，用现有的权重减去这个部分，得到新的权重参数(因为梯度表示变化率最大的增大方向，减去这个值之后，损失函数值才会下降)。

记x为权重参数向量x，而梯度为dx，然后我们设定学习率为learning_rate，则最简单的参数更新如下：

# Vanilla update
x += - learning_rate * dx

当然learning_rate是我们自己设定的一个超变量值(在该更新方法中是全程不变的)，而且数学上可以保证，当学习率足够低的时候，经这个过程迭代后，损失函数不会增加。

Momentum update

这是上面参数更新方法的一种小小的优化，通常说来，在深层次的神经网络中，收敛效率更高一些(速度更快)。这种参数更新方式源于物理学角度的优化。

# 物理动量角度启发的参数更新
v = mu * v - learning_rate * dx # 合入一部分附加速度
x += v # 更新参数

这里v是初始化为0的一个值，mu是我们敲定的另外一个超变量(最常见的设定值为0.9，物理含义和摩擦力系数相关)。

一个比较粗糙的理解是，(随机)梯度下降可以看做从山上下山到山底的过程，这种方式，相当于在下山的过程中，加上了一定的摩擦阻力，消耗掉一小部分动力系统的能量，这样会比较高效地在山底停住，而不是持续震荡。

其实我们也可以用交叉验证来选择最合适的mu值，一般我们会从[0.5, 0.9, 0.95, 0.99]里面选出最合适的。

Nesterov Momentum

这是momentum update的一个不同的版本，最近也用得很火。

据称，这种参数更新方法，有更好的凸函数和凸优化理论基础，而实际中的收敛效果也略优于momentum update。

它的思想对应着如下的代码：

x_ahead = x + mu * v
#考虑到这个时候的x已经有一些变化了
v = mu * v - learning_rate * dx_ahead
x += v

工程上更实用的一个版本是：

v_prev = v # 当前状态先存储起来
v = mu * v - learning_rate * dx # 依旧按照Momentum update的方式更新
x += -mu * v_prev + (1 + mu) * v # 新的更新方式

1.4.2 衰减学习率

在实际训练过程中，随着训练过程推进，逐渐衰减学习率是很有必要的。

我们继续回到下山的场景中，刚下山的时候，可能离最低点很远，那我步子迈大一点也没什么关系，可是快到山脚了，我还激进地大步飞奔，一不小心可能就迈过去了。所以还不如随着下山过程推进，逐步减缓一点点步伐。

不过这个『火候』确实要好好把握，衰减太慢的话，最低段震荡的情况依旧；衰减太快的话，整个系统下降的『动力』衰减太快，很快就下降不动了。下面提一些常见的学习率衰减方式：

步伐衰减：这是很常见的一个衰减模式，每过一轮完整的训练周期(所有的图片都过了一遍)之后，学习率下降一些。

比如比较常见的一个衰减率可能是每20轮完整训练周期，下降10%。不过最合适的值还真是依问题不同有变化。

如果你在训练过程中，发现交叉验证集上呈现很高的错误率，还一直不下降，你可能就可以考虑考虑调整一下(衰减)学习率了。

指数级别衰减：数学形式为\(\alpha=\alpha_{0} e^{-k t}\)，其中\(\alpha_{0}, k\)是需要自己设定的超参数，t 是迭代轮数。

1/t衰减：有着数学形式为\(\alpha=\alpha_{0} /(1+k t)\)的衰减模式，其中\(\alpha_{0}, k\)是需要自己设定的超参数，t 是迭代轮数。

实际工程实践中，大家还是更倾向于使用步伐衰减，因为它包含的超参数少一些，计算简单一些，可解释性稍微高一点。

1.4.3 二次迭代方法

最优化问题里还有一个非常有名的牛顿法，它按照如下的方式进行迭代更新参数：

$x \leftarrow x-[H f(x)]^{-1} \nabla f(x)$

这里的\(H f(x)\)是Hessian矩阵，是函数的二阶偏微分。

而\(\nabla f(x)\)和梯度下降里看到的一样，是一个梯度向量。

直观理解是Hessian矩阵描绘出了损失函数的曲度，因此能让我们更高效地迭代和靠近最低点：乘以Hessian矩阵进行参数迭代会让在曲度较缓的地方，会用更激进的步长更新参数，而在曲度很陡的地方，步伐会放缓一些。

因此相对一阶的更新算法，在这点上它还是有很足的优势的。

比较尴尬的是，实际深度学习过程中，直接使用二次迭代的方法并不是很实用。原因是直接计算Hessian矩阵是一个非常耗时耗资源的过程。

举个例子说，一个一百万参数的神经网络的Hessian矩阵维度为[1000000*1000000]，算下来得占掉3725G的内存。

当然，我们有L-BFGS这种近似Hessian矩阵的算法，可以解决内存问题。

但是L-BFGS一般在全部数据集上计算，而不像我们用的mini-batch SGD一样在小batch上迭代。

现在有很多人在努力研究这个问题，试图让L-BFGS也能以mini-batch的方式稳定迭代更新。但就目前而言，大规模数据上的深度学习很少用到L-BFGS或者类似的二次迭代方法，倒是随机梯度下降这种简单的算法被广泛地使用着。

1.4.4 逐参更新学习率

到目前为止大家看到的学习率更新方式，都是全局使用同样的学习率。

调整学习率是一件很费时同时也容易出错的事情，因此大家一直希望有一种学习率自更新的方式，甚至可以细化到逐参数更新。

现在确实有一些这种方法，其中大多数还需要额外的超参数设定，优势是在大多数超参数设定下，效果都比使用写死的学习率要好。

Adagrad是Duchi等在论文"Adaptive Subgradient Methods for Online Learning and Stochastic Optimization"中提出的自适应学习率算法。简单代码实现如下：

# 假定梯度为dx，参数向量为x
cache += dx**2
x += - learning_rate * dx / np.sqrt(cache + 1e-8)

其中变量cache有着和梯度一样的维度，然后我们用这个变量持续累加梯度平方。

之后这个值被用作参数更新步骤中的归一化。

这种方法的好处是，对于高梯度的权重，它们的有效学习率被降低了；而小梯度的权重迭代过程中学习率提升了。

而分母开根号这一步非常重要，不开根号的效果远差于开根号的情况。

平滑参数1e-8避免了除以0的情况。

RMSprop是一种非常有效，然而好像还没有被公开发布的自适应学习率更新方法。

有意思的是，现在使用这个方法的人，都引用的大神Geoff Hinton的coursera课程第6节的讲义第29页。

RMSProp方法对Adagrad算法做了一个简单的优化，以减缓它的迭代强度，它开方的部分cache做了一个平滑处理，大致的示意代码如下：

cache = decay_rate * cache + (1 - decay_rate) * dx**2
x += - learning_rate * dx / np.sqrt(cache + 1e-8)

这里的decay_rate是一个手动设定的超参数，我们通常会在[0.9, 0.99, 0.999]中取值。需要特别注意的是，x+=这个累加的部分和Adagrad是完全一样的，但是cache本身是迭代变化的。

另外的方法还有：

• Matthew Zeiler提出的Adadelta
• Adam: A Method for Stochastic Optimization
• Unit Tests for Stochastic Optimization

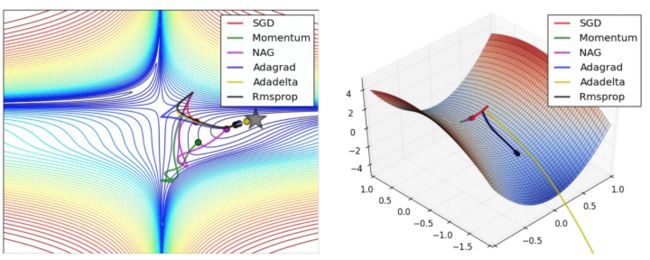
下图是上述提到的多种参数更新方法下，损失函数最优化的示意图：

1.5 超参数的设定与优化

神经网络的训练过程中，不可避免地要和很多超参数打交道，这是我们需要手动设定的，大致包括：

• 初始学习率
• 学习率衰减程度
• 正则化系数/强度(包括l2正则化强度，dropout比例)

对于大的深层次神经网络而言，我们需要很多的时间去训练。因此在此之前我们花一些时间去做超参数搜索，以确定最佳设定是非常有必要的。

最直接的方式就是在框架实现的过程中，设计一个会持续变换超参数实施优化，并记录每个超参数下每一轮完整训练迭代下的验证集状态和效果。

实际工程中，神经网络里确定这些超参数，我们一般很少使用n折交叉验证，一般使用一份固定的交叉验证集就可以了。

一般对超参数的尝试和搜索都是在log域进行的。

例如，一个典型的学习率搜索序列就是learning_rate = 10 ** uniform(-6, 1)。我们先生成均匀分布的序列，再以10为底做指数运算，其实我们在正则化系数中也做了一样的策略。

比如常见的搜索序列为[0.5, 0.9, 0.95, 0.99]。另外还得注意一点，如果交叉验证取得的最佳超参数结果在分布边缘，要特别注意，也许取的均匀分布范围本身就是不合理的，也许扩充一下这个搜索范围会有更好的参数。

1.6 模型融合与优化

实际工程中，一个能有效提高最后神经网络效果的方式是，训练出多个独立的模型，在预测阶段选结果中的众数。

模型融合能在一定程度上缓解过拟合的现象，对最后的结果有一定帮助，我们有一些方式可以得到同一个问题的不同独立模型：

使用不同的初始化参数。先用交叉验证确定最佳的超参数，然后选取不同的初始值进行训练，结果模型能有一定程度的差别。

选取交叉验证排序靠前的模型。在用交叉验证确定超参数的时候，选取top的部分超参数，分别进行训练和建模。

选取训练过程中不同时间点的模型。神经网络训练确实是一件非常耗时的事情，因此有些人在模型训练到一定准确度之后，取不同的时间点的模型去做融合。不过比较明显的是，这样模型之间的差异性其实比较小，好处是一次训练也可以有模型融合的收益。

还有一种常用的有效改善模型效果的方式是，对于训练后期，保留几份中间模型权重和最后的模型权重，对它们求一个平均，再在交叉验证集上测试结果。

通常都会比直接训练的模型结果高出一两个百分点。

直观的理解是，对于碗状的结构，有很多时候我们的权重都是在最低点附近跳来跳去，而没法真正到达最低点，而两个最低点附近的位置求平均，会有更高的概率落在离最低点更近的位置。

2. 总结

• 用一部分的数据测试你梯度计算是否正确，注意提到的注意点。
• 检查你的初始权重是否合理，在关掉正则化项的系统里，是否可以取得100%的准确度。
• 在训练过程中，对损失函数结果做记录，以及训练集和交叉验证集上的准确度。
• 最常见的权重更新方式是SGD+Momentum，推荐试试RMSProp自适应学习率更新算法。
• 随着时间推进要用不同的方式去衰减学习率。
• 用交叉验证等去搜索和找到最合适的超参数。
• 记得也做做模型融合的工作，对结果有帮助。

转载于:https://www.cnblogs.com/Terrypython/p/11018383.html