PCA学习过程遇到的问题

PCA学习过程遇到的问题
目录
1、遇到的问题。
2、解决方法。

1、遇到的问题。
在学习PCA时遇到这个公式

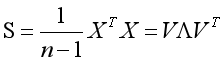
S是样本协方差矩阵，于是打算用代码测试一下。
数据如下

X=np.array([[1 ,5 ,6] ,[4 ,3 ,9 ],[ 4 ,2 ,9],[ 4 ,7 ,2]])

样本的协方差矩阵S用np求出。

x2 = np.cov(X.T)
print(x2)

得出如下结果
[[ 2.25 -0.75 0.5 ]
[-0.75 4.91666667 -7.16666667]
[ 0.5 -7.16666667 11. ]]
用(X_T*X)/(N-1)方法求解

Y = np.dot(X.T,X)/(3)
print(Y)

结果如下
[[16.33333333 17.66666667 28.66666667]
[17.66666667 29. 29.66666667]
[28.66666667 29.66666667 67.33333333]]
发现两种方法求出的结果并不相同。

2、解决方法
重新思考协方差矩阵的求解过程发现问题，采用如下代码就可实现结果一致。

def norm_(x):
    xmean = np.mean(x,0)
    return (x-xmean)
data_ = norm_(X)
x3 = np.dot(data_.T,data_)/(3)
print('另一种方式的协方差')
print(x3)

结果如下：
另一种方式的协方差
[[ 2.25 -0.75 0.5 ]
[-0.75 4.91666667 -7.16666667]
[ 0.5 -7.16666667 11. ]]
和直接用 x2 = np.cov(X.T)结果相同。
刚开始出现问题是因为原始数据如果单纯矩阵相乘的话数据并没有去均值化。

进一步思考，在PCA用于数据降维时，一般都会对数据进行标准化预处理,代码如下：

# normalization
def norm_(x):
    xmean = np.mean(x,0)
    std = np.std(x,0)
    return (x-xmean)/std
data_ = norm_(X)
x4 = np.dot(data_.T,data_)/(3)
print('方差')
print(x4)
x5 = np.cov(data_.T)
print('另一种方式的协方差')
print(x5)

方差
[[ 1.33333333 -0.30065841 0.13400504]
[-0.30065841 1.33333333 -1.29934421]
[ 0.13400504 -1.29934421 1.33333333]]
另一种方式的协方差
[[ 1.33333333 -0.30065841 0.13400504]
[-0.30065841 1.33333333 -1.29934421]
[ 0.13400504 -1.29934421 1.33333333]]

发现两者结果相同，顾数据预处理之后就不会出现刚开始存在的疑惑了。