主成分分析（PCA）过程监测和故障识别-----Python实现

目录
1、目标
2、生成数据
3、对正常数据建立PCA模型
4、测试故障数据并画图
5、计算贡献率图

1、目标
有两组数据，一组正常数据，一组故障数据，通过对正常数据建立PCA模型，通过模型监测出故障数据。

2、生成数据
正常数据是一个400*4的矩阵，测试数据相对于正常数据在第二列后50个数据上发生变化

#生成正常数据
num_sample=100
a = 10*np.random.randn(num_sample, 1)
x1 = a + np.random.randn(num_sample, 1)
x2 = 1*np.sin(a) + np.random.randn(num_sample, 1)
x3 = 5*np.cos(5*a) +np.random.randn(num_sample, 1)
x4 = 0.8*x2 + 0.1*x3+np.random.randn(num_sample, 1)
x = np.c_[x1,x2,x3,x4]
xx_train=x

#产生测试集
a = 10*np.random.randn(num_sample, 1)
x1 = a + np.random.randn(num_sample, 1)
x2 = 1*np.sin(a) + np.random.randn(num_sample, 1)
x3 = 5*np.cos(5*a) +np.random.randn(num_sample, 1)
x4 = 0.8*x2 + 0.1*x3+np.random.randn(num_sample, 1)
xx_test = np.c_[x1,x2,x3,x4]
xx_test[50:,1]=xx_test[50:,1]+15

Xtrain =xx_train
Xtest =xx_test

3、对正常数据建立PCA模型
下面代码包括了对数据的预处理和建立PCA模型以及阈值的求解

def PCA(data):
    data_mean = np.mean(data,0)
    data_std = np.std(data,0)
    data_nor = (data - data_mean)/data_std
    X = np.cov(data_nor.T)
    P,v,P_t = np.linalg.svd(X)  #载荷矩阵计算  此函数返回三个值 u s v 此时v是u的转置
    Z = np.dot(P,P_t)
    v_sum = np.sum(v)
    k = []##主元个数
    for x in range(len(v)):
        PE_k = v[x]/v_sum
        if x == 0:
            PE_sum = PE_k 
        else:
            PE_sum = PE_sum + PE_k
        if PE_sum < 0.85:   #累积方差贡献率
            pass
        else:
            k.append(x+1)
            print(k)
            break
	##新主元
    p_k = P[:,:k[0]]
    v_I = np.diag(1/v[:k[0]])
    ##T统计量阈值计算
    coe = k[0]*(np.shape(data)[0]-1)*(np.shape(data)[0]+1)/((np.shape(data)[0]-k[0])*np.shape(data)[0])
    T_95_limit = coe*stats.f.ppf(0.95,k[0],(np.shape(data)[0]-k[0]))
    T_99_limit = coe*stats.f.ppf(0.99,k[0],(np.shape(data)[0]-k[0]))
    ##SPE统计量阈值计算
    O1 = np.sum((v[k[0]:])**1)
    O2 = np.sum((v[k[0]:])**2)
    O3 = np.sum((v[k[0]:])**3)
    h0 = 1 - (2*O1*O3)/(3*(O2**2))
    c_95 = 1.645
    c_99 = 2.325
    SPE_95_limit = O1*((h0*c_95*((2*O2)**0.5)/O1 + 1 + O2*h0*(h0-1)/(O1**2))**(1/h0))
    SPE_99_limit = O1*((h0*c_99*((2*O2)**0.5)/O1 + 1 + O2*h0*(h0-1)/(O1**2))**(1/h0)）
    return v_I, p_k, data_mean, data_std, T_95_limit, T_99_limit, SPE_95_limit, SPE_99_limit,v,P,k
 v_I, p_k, data_mean, data_std, T_95_limit, T_99_limit, SPE_95_limit, SPE_99_limit,v,P,k = PCA(Xtrain)

4、测试故障数据并画图

#计算T统计量
def T2(data_in, data_mean, data_std, p_k, v_I):
    test_data_nor = ((data_in - data_mean)/data_std).reshape(len(data_in),1)
    T_count = np.dot(np.dot((np.dot((np.dot(test_data_nor.T,p_k)), v_I)), p_k.T),test_data_nor)
    return T_count
 #计算SPE统计量
def SPE(data_in, data_mean, data_std, p_k):
    test_data_nor = ((data_in - data_mean)/data_std).reshape(len(data_in),1)
    I = np.eye(len(data_in))
    Q_count = np.dot(np.dot((I - np.dot(p_k, p_k.T)), test_data_nor).T,np.dot((I - np.dot(p_k, p_k.T)), test_data_nor))
    #Q_count = np.linalg.norm(np.dot((I - np.dot(p_k, p_k.T)), test_data_nor), ord=None, axis=None, keepdims=False)
    return Q_count
 #循环计算
test_data = Xtest
t_total = []
q_total = []
for x in range(np.shape(test_data)[0]):
    data_in = Xtest[x,:]
    t = T2(data_in, data_mean, data_std, p_k, v_I)
    q = SPE(data_in, data_mean, data_std, p_k)
    t_total.append(t[0,0])
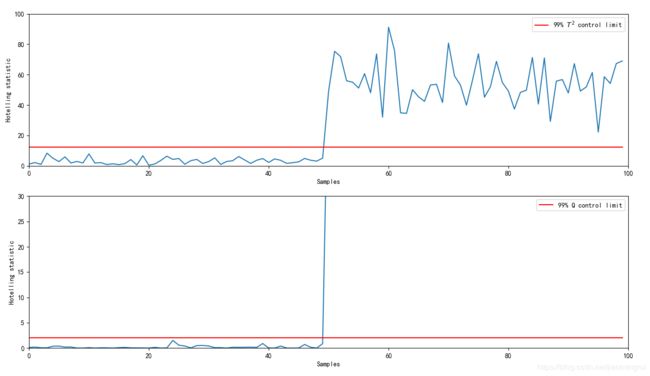
    q_total.append(q[0,0])

对求出的T2和Q统计量进行过作图

##画图
plt.figure(2,figsize=(16,9))
ax1=plt.subplot(2,1,1)
plt.plot(t_total)
plt.plot(np.ones((len(test_data)))*T_99_limit,'r',label='99% $T^2$ control limit')
ax1.set_ylim(0,100)
plt.xlim(0,100)
ax1.set_xlabel(u'Samples')
ax1.set_ylabel(u'Hotelling statistic')
plt.legend()
plt.show
ax1=plt.subplot(2,1,2)
plt.plot(q_total)
plt.plot(np.ones((len(test_data)))*SPE_99_limit,'r',label='99% Q control limit')
ax1.set_ylim(0,30)
plt.xlim(0,100)
ax1.set_xlabel(u'Samples')
ax1.set_ylabel(u'Hotelling statistic')
plt.legend()
plt.show

结果如图：

5、计算贡献率图

#%%
#贡献图
index = 50
#1.确定造成失控状态的得分
test_data = Xtest
test_data_submean = test_data-data_mean
test_data_norm = (test_data - data_mean)/data_std
t = test_data_norm[index,:].reshape(1,test_data.shape[1])
S = np.dot(t,p_k[:,:])
r = []
for i in range(k[0]):
    if S[0,i]**2/v[i] > T_99_limit/k[0]:
        r.append(i)
print(r)
#2.计算每个变量相对于上述失控得分的贡献
cont = np.zeros([len(r),test_data.shape[1]])
for i in range(len(r)):
    for j in range(test_data.shape[1]):
        cont[i,j] = S[0,i]/v[r[i]]*P[r[i],j]*test_data_submean[index,j]
        if cont[i,j] < 0:
            cont[i,j] = 0
#3.计算每个变量对T的总贡献
a = cont.sum(axis = 0)
#4.计算每个变量对Q的贡献
I = np.eye(test_data.shape[1])
e = (np.dot(test_data_norm[index,:],(I - np.dot(p_k, p_k.T))))**2

a为求得的CONT贡献率数据，e为求得的RES贡献率数据。将这两个数据作图如下

##画图
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
font1 = {'family' : 'SimHei','weight' : 'normal','size'   : 23,}
plt.figure(2,figsize=(16,9))
ax1=plt.subplot(2,1,1)
plt.bar(range(len(data_in)),a)
plt.xlabel(u'变量号',font1)
plt.ylabel(u'T^2贡献率 %',font1)
plt.legend()
plt.show
ax1=plt.subplot(2,1,2)
plt.bar(range(len(data_in)),e)
plt.xlabel(u'变量号',font1)
plt.ylabel(u'Q贡献率 %',font1)
plt.legend()
plt.show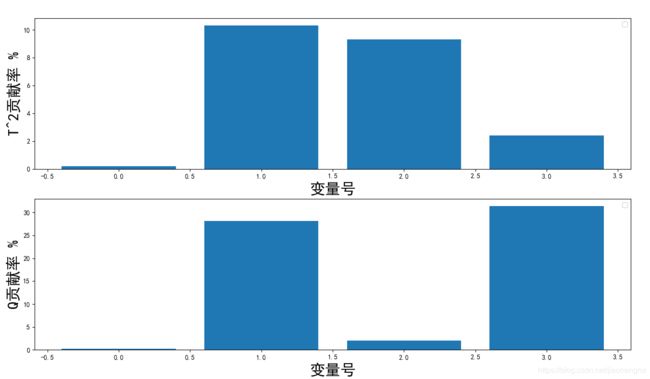

总结
1、通过对正常数据建立PCA模型，建立T2和Q统计量阈值，可以对故障实现监测。
2、当监测到故障发生后，可以通过贡献率图确定哪一个变量对故障发生起主导作用。

Reference:
1、主成分分析（PCA）原理与故障诊断（SPE、T^2以及结合二者的综合指标）-MATLAB实现https://blog.csdn.net/u013829973/article/details/77981701
2、基于主成分分析（PCA）的故障诊断（SPE和T^2指标）-MATLAB实现https://blog.csdn.net/qq_44744164/article/details/105794851

全部代码可以在这里获得：
https://download.csdn.net/download/jiaohengrui/12522367