基于LDA的人脸识别算法研究

一．实验背景：

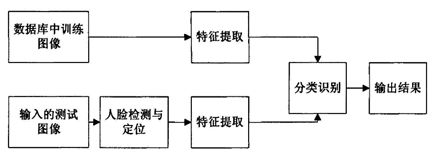
一个完整的人脸识别系统包括人脸检测与定位、人脸特征提取、分类识别等，如图1所示。

图1 人脸识别系统

研究者们从各种不同的途径提出了多种方法，其中主要有：基于模板匹配的方法，基于知识的人脸验证的方法，以及目前比较流行的基于统计的学习方法和基于神经网络的方法等。在基于统计方法的识别方法中，PCA、LDA方法是利用测试图像在特定子空间上投影向量作为特征向量，本文重点介绍了基于线性判别分析（LDA）原理的人脸识别技术。线性判别分析是一种传统的用于特征提取的线性分类的方法。本文重点研究了基于 LDA 人脸识别的算法，并对该算法进行了实验验证与分析，实验结果表明该算法能有效提鉴别别信息，具有较高的识别率。

二．实验要求：

采用自己编写的LDA算法，对ORL人脸库进行识别，用10折交叉验证的方法计算准确率，并对结果进行分析。

三．算法/素材介绍：

①LDA算法介绍：

  线性判别分析（LDA）技术，它是以对样本进行很好的分类为目的，充分利用了训练样本已知的类别信息，寻找最有助于分类的投影方向子空间，属于监督学习方法。

经典的LDA采用Fisher判别准则函数，因此也成为FLD，最早由Fisher在1936年提出，基本思想是寻找是Fisher准则达到极大值的向量作为最佳投影方向，使投影后的样本能达到最大的类间离散度和最小的类内离散度，使投影后样本具有最佳的可分离性，是一种有效用于分类的特征提取方法。利用Fisher准则，当Sw非奇异，可以通过对Sw-1Sb进行特征值分解，从而求出最佳投影方向W（Sw：本的类内离散度矩阵，Sb：样本类间离散度矩阵）。但是当LDA用于人脸特征提取时，因图像转换为列向量维数太大，往往远大于样本数，造成Sw奇异，很难解出最佳投影方向，即小样本问题，所以先利用PCA技术对人脸图像进行降维，使Sw满秩，再利用LDA技术对其进行特征提取，进而进行人脸识别，是一种较经典的解决LDA用于人脸识别时遇到的小样本问题的方法，称为Fisherfaces方法或PCA+LDA方法。

②10折交叉验证算法：

我们把每个数据集分成两个子集

- 一个用于构建分类器，该数据集称为训练集（training set）

• 另一个数据集用于评估分类器，该数据集称为测试集（test set）

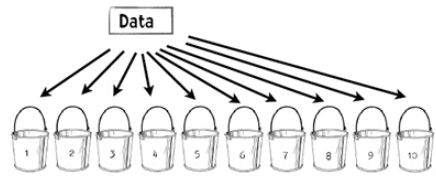
图2数据分类图

我们可以将数据划分成10部分，每次利用9/10的数据训练而在其余1/10的数据上进行测试。因此，整个过程看起来如下：

第一次迭代 使用Part 1～Part 9训练，使用Part
10测试

第二次迭代 使用Part 1～Part 8，Part10训练，使用Part 9测试

第三次迭代 使用Part 1和Part 7，Part9～Part10训练，使用Part 8测试

对上述结果求平均。

在数据挖掘中，最常用的划分数目是10，这种方法称为10折交叉验证（10-fold
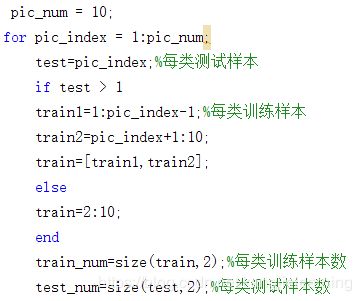
Cross Validation）使用这种方法，我们将数据集随机分成10份，使用其中9份进行训练而将另外1份用作测试。该过程可以重复10次，每次使用的测试数据不同。在程序中，通过一个for循环对数据进行分类，分类程序见图3。

图3数据集分类

③实验素材介绍：

ORL人脸数据库由剑桥大学AT＆T实验室创建，其中包含40个人的不同图像。有些人的图像是在不同的时间、不同的光线、不同的表情（睁眼/闭眼，笑/不笑）下拍摄的。其中人脸姿态也有很大的变化，其深度旋转和平面旋转可达20度。人脸的尺寸也有不超过10%的变化。ORL人脸库见图4。

图4 ORL人脸库

四．实验步骤：

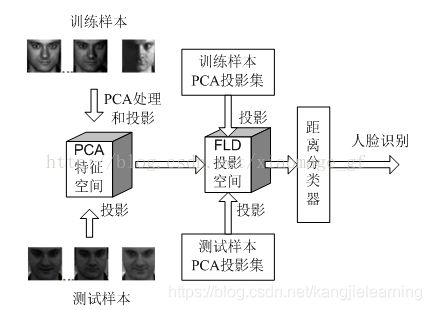
先利用PCA降维，再利用LDA寻找最优投影向量，在ORL上测试，采用10折交叉算法验证不同训练集对识别率的影响，并寻找最佳投影维数，最后输出识别率。程序流程图见图5，步骤图见图6。

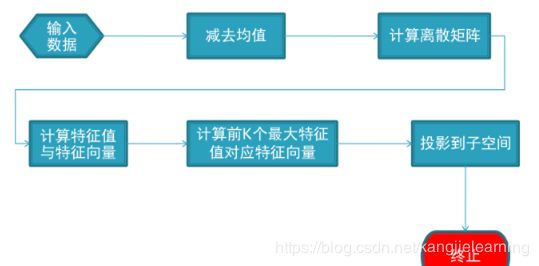
图5程序流程图

图6实验步骤图

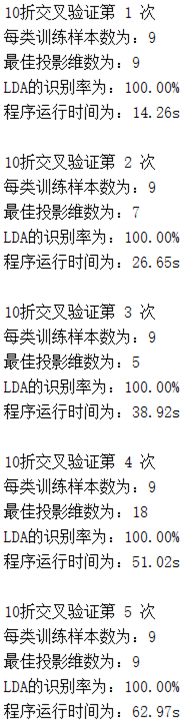
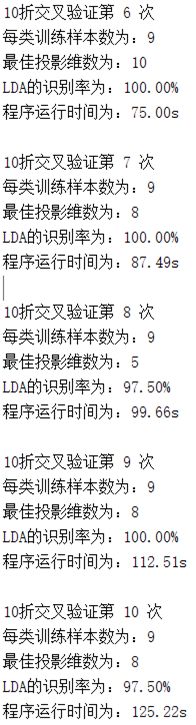
进行 matlab 的仿真得出实验的结果，主要是研究了用 PCA 方法对人脸进行特征的提取，用经过改进后的 LDA方法算出真确的人脸识别率，先用 PCA 方法降维，在用标准的 LDA 方法进行识别，这是本实验的目的。同时用10折交叉验证的方法验证LDA算法的准确率。

五．实验结果：

图7实验结果图

六．结论：

在PCA算法的基础上，运用LDA算法对ORL人脸库进行识别，最后通过十折交叉验证算法对LDA算法的准确率进行验证，得到的识别率在97.5%～100%之间，取十次的准确率的均值99.5%作为LDA算法识别ORL人脸库准确率的估计，所以LDA算法对ORL人脸库的识别是较准确的。

程序：
①读取样本函数

function sample=readsample(address,classnum,num)
%这个函数用来读取样本。
%输入：address就是要读取的样本的地址,classnum代表要读入样本的类别,num是每类的样本；
%输出为样本矩阵
allsamples=[];
image=imread([pwd '\ORL\s1_1.bmp']);%读入第一幅图像
[rows cols]=size(image);%获得图像的行数和列数
for i=classnum
    for j=num
        a=imread(strcat(address,num2str(i),'_',num2str(j),'.bmp'));
        b=a(1:rows*cols);
        b=double(b);
        allsamples=[allsamples;b];
    end
end
sample=allsamples;

②计算Sw，Sb

function [sw
sb]=computswb(samples,classnum,num)

%计算sw，sb

%samples为输入的样本，classnum为类别数，num为每一类的样本数

%输出sw为类内协方差矩阵，sb为类间协方差矩阵。

samplemean=mean(samples);

for i=1:classnum%类别数

   
newsamplemean(i,:)=mean(samples((i-1)*num+1:i*num,:));

end

sw=0;

for i=1:classnum

   
for j=1:num

       
sw=sw+(samples((i-1)*num+j,:)-newsamplemean(i,:))'*(samples((i-1)*num+j,:)-newsamplemean(i,:));

   
end

end

sb=0;

for i=1:classnum

   
sb=sb+(newsamplemean(i,:)-samplemean)'*(newsamplemean(i,:)-samplemean);

end

③计算计算sw/sb投影的最优向量

function vsort=projectto(sw,sb,num)

%计算sw/sb投影的最优向量

%sw为类内协方差矩阵，sb是类间协方差矩阵

%vsort为最优投影向量

invSw=inv(sw);

newspace=invSw*sb;

[x y]=eig(newspace);

d=diag(y);

[d1 index1]=dsort(d);

for i=1:num

   
vsort(:,i)=x(:,index1(i));

end

④主分量分析程序

function [newsample basevector]=pca(patterns,num)

%主分量分析程序，patterns表示输入模式向量，num为控制变量，当num大于1的时候表示

%要求的特征数为num，当num大于0小于等于1的时候表示求取的特征数的能量为num

%输出：basevector表示求取的最大特征值对应的特征向量，newsample表示在basevector

%映射下获得的样本表示。

[u v]=size(patterns);

totalsamplemean=mean(patterns);

for i=1:u

   
gensample(i,:)=patterns(i,:)-totalsamplemean;

end

sigma=gensample*gensample';

[U V]=eig(sigma);

d=diag(V);

[d1 index]=dsort(d);

if num>1

   
for i=1:num

       
vector(:,i)=U(:,index(i));

       
base(:,i)=d(index(i))^(-1/2)* gensample' * vector(:,i);

   
end

else

   
sumv=sum(d1);

   
for i=1:u

       
if sum(d1(1:i))/sumv>=num

           
l=i;

           
break;

       
end

   
end

   
for i=1:l

       
vector(:,i)=U(:,index(i));

       
base(:,i)=d(index(i))^(-1/2)* gensample' * vector(:,i);

   
end

end

newsample=patterns*base;

basevector=base;

⑤计算准确率的函数

function accuracy=computaccu(testsample,num1,trainsample,num2)

%计算准确率的函数

%输入testsample表示经过投影后的测试样本,num1表示每一类测试样本的个数,

%trainsample代表经过投影后的训练样本,num2代表每一类训练样本的个数

%输出为正确率

accu=0;

testsampnum=size(testsample,1);

trainsampnum=size(trainsample,1);

for i=1:testsampnum

    for j=1:trainsampnum

       
juli(j)=norm(testsample(i,:)-trainsample(j,:));

    end

    [temp index]=sort(juli);

    if
ceil(i/num1)==ceil(index(1)/num2)

        accu=accu+1;

    end

end

accuracy=accu/testsampnum;

⑥主函数

clear all

clc

close all

start=clock;

sample_class=1:40;%样本类别

sample_classnum=size(sample_class,2);%样本类别数

fprintf('程序运行开始....................\n\n');

 pic_num = 10;

for pic_index = 1:pic_num;

   
test=pic_index;%每类测试样本

    if test > 1

   
train1=1:pic_index-1;%每类训练样本

   
train2=pic_index+1:10;

   
train=[train1,train2];

    else

    train=2:10;

    end

   
train_num=size(train,2);%每类训练样本数

   
test_num=size(test,2);%每类测试样本数

    address=[pwd
'\ORL\s'];

    %读取训练样本

   
allsamples=readsample(address,sample_class,train);

        %先使用PCA进行降维

    [newsample
base]=pca(allsamples,0.9);

    %计算Sw,Sb

    [sw
sb]=computswb(newsample,sample_classnum,train_num);

    

    %读取测试样本

   
testsample=readsample(address,sample_class,test);

    best_acc=0;%最优识别率

    %寻找最佳投影维数

    for
temp_dimension=1:1:length(sw)

       
vsort1=projectto(sw,sb,temp_dimension);

        

        %训练样本和测试样本分别投影

       
tstsample=testsample*base*vsort1;

       
trainsample=newsample*vsort1;

        %计算识别率

       
accuracy=computaccu(tstsample,test_num,trainsample,train_num);

        if
accuracy>best_acc

           
best_dimension=temp_dimension;%保存最佳投影维数

            best_acc=accuracy;

        end

    end

   
%---------------------------------输出显示----------------------------------

    fprintf('10折交叉验证第 %d 次 \n',pic_index);

    fprintf('每类训练样本数为：%d\n',train_num);

    fprintf('最佳投影维数为：%d\n',best_dimension);

    fprintf('LDA的识别率为：%.2f%%\n',best_acc*100);

    fprintf('程序运行时间为：%3.2fs\n\n',etime(clock,start)); end

fprintf('程序运行结束....................\n\n');