cs231n assignment2 FullyConnectedNets
Affine layer: foward
import time
import numpy as np
import matplotlib.pyplot as plt
from cs231n_2.classifiers.fc_net import *
from cs231n_2.data_utils import get_CIFAR10_data
from cs231n_2.gradient_check import eval_numerical_gradient, eval_numerical_gradient_array
from cs231n_2.solver import Solver
def rel_error(x, y):
return np.max(np.abs(x - y) / (np.maximum(1e-8, np.abs(x) + np.abs(y))))
# Affine layer: foward
num_inputs = 2
input_shape = (4, 5, 6)
output_dim = 3
input_size = num_inputs * np.prod(input_shape) # np.prod() 求乘积
weight_size = output_dim * np.prod(input_shape)
x = np.linspace(-0.1, 0.5, num=input_size).reshape(num_inputs, *input_shape) # (2,4,5,6) # np.linspace() 生成等差数列
w = np.linspace(-0.2, 0.3, num=weight_size).reshape(np.prod(input_shape), output_dim) # (120,3)
b = np.linspace(-0.3, 0.1, num=output_dim)
out, _ = affine_forward(x, w, b)
correct_out = np.array([[ 1.49834967, 1.70660132, 1.91485297],
[ 3.25553199, 3.5141327, 3.77273342]])
# Compare your output with ours. The error should be around e-9 or less.
print('Testing affine_forward function:')
print('difference: ', rel_error(out, correct_out))affine_forward 实现:
def affine_forward(x, w, b):
out = None
###########################################################################
# TODO: Implement the affine forward pass. Store the result in out. You #
# will need to reshape the input into rows. #
###########################################################################
# x = x.reshape(x.shape[0], -1)
out = np.dot(x.reshape(x.shape[0], -1), w) + b
###########################################################################
# END OF YOUR CODE #
###########################################################################
cache = (x, w, b)
return out, cacheAffine layer: backward
# Test the affine_backward function
np.random.seed(231)
x = np.random.randn(10, 2, 3)
w = np.random.randn(6, 5)
b = np.random.randn(5)
dout = np.random.randn(10, 5)
dx_num = eval_numerical_gradient_array(lambda x: affine_forward(x, w, b)[0], x, dout)
dw_num = eval_numerical_gradient_array(lambda w: affine_forward(x, w, b)[0], w, dout)
db_num = eval_numerical_gradient_array(lambda b: affine_forward(x, w, b)[0], b, dout)
_, cache = affine_forward(x, w, b)
dx, dw, db = affine_backward(dout, cache)
# The error should be around e-10 or less
print('Testing affine_backward function:')
print('dx error: ', rel_error(dx_num, dx))
print('dw error: ', rel_error(dw_num, dw))
print('db error: ', rel_error(db_num, db))affine_backward 实现:
def affine_backward(dout, cache):
x, w, b = cache
dx, dw, db = None, None, None
###########################################################################
# TODO: Implement the affine backward pass. #
###########################################################################
dx = np.dot(dout, w.T)
dw = np.dot(x.reshape(x.shape[0], -1).T, dout)
db = np.sum(dout, axis=0)
dx = dx.reshape(x.shape)
###########################################################################
# END OF YOUR CODE #
###########################################################################
return dx, dw, db
ReLU activation: forward
# Test the relu_forward function
x = np.linspace(-0.5, 0.5, num=12).reshape(3, 4)
out, _ = relu_forward(x)
correct_out = np.array([[ 0., 0., 0., 0., ],
[ 0., 0., 0.04545455, 0.13636364,],
[ 0.22727273, 0.31818182, 0.40909091, 0.5, ]])
# Compare your output with ours. The error should be on the order of e-8
print('Testing relu_forward function:')
print('difference: ', rel_error(out, correct_out))
np.random.seed(231)
x = np.random.randn(10, 10)
dout = np.random.randn(*x.shape)
dx_num = eval_numerical_gradient_array(lambda x: relu_forward(x)[0], x, dout)
_, cache = relu_forward(x)
dx = relu_backward(dout, cache)
# The error should be on the order of e-12
print('Testing relu_backward function:')
print('dx error: ', rel_error(dx_num, dx))relu_forward 实现:
def relu_forward(x):
out = None
###########################################################################
# TODO: Implement the ReLU forward pass. #
###########################################################################
out = np.maximum(0, x)
###########################################################################
# END OF YOUR CODE #
###########################################################################
cache = x
return out, cacheReLU activation: backward
def relu_backward(dout, cache):
dx, x = None, cache
###########################################################################
# TODO: Implement the ReLU backward pass. #
###########################################################################
dx = dout
dx[x <= 0] = 0
###########################################################################
# END OF YOUR CODE #
###########################################################################
return dx
"Sandwich" layers
from cs231n.layer_utils import affine_relu_forward, affine_relu_backward
np.random.seed(231)
x = np.random.randn(2, 3, 4)
w = np.random.randn(12, 10)
b = np.random.randn(10)
dout = np.random.randn(2, 10)
out, cache = affine_relu_forward(x, w, b)
dx, dw, db = affine_relu_backward(dout, cache)
dx_num = eval_numerical_gradient_array(lambda x: affine_relu_forward(x, w, b)[0], x, dout)
dw_num = eval_numerical_gradient_array(lambda w: affine_relu_forward(x, w, b)[0], w, dout)
db_num = eval_numerical_gradient_array(lambda b: affine_relu_forward(x, w, b)[0], b, dout)
# Relative error should be around e-10 or less
print('Testing affine_relu_forward and affine_relu_backward:')
print('dx error: ', rel_error(dx_num, dx))
print('dw error: ', rel_error(dw_num, dw))
print('db error: ', rel_error(db_num, db))Loss layers: Softmax and SVM
np.random.seed(231)
num_classes, num_inputs = 10, 50
x = 0.001 * np.random.randn(num_inputs, num_classes)
y = np.random.randint(num_classes, size=num_inputs)
dx_num = eval_numerical_gradient(lambda x: svm_loss(x, y)[0], x, verbose=False)
loss, dx = svm_loss(x, y)
# Test svm_loss function. Loss should be around 9 and dx error should be around the order of e-9
print('Testing svm_loss:')
print('loss: ', loss)
print('dx error: ', rel_error(dx_num, dx))
dx_num = eval_numerical_gradient(lambda x: softmax_loss(x, y)[0], x, verbose=False)
loss, dx = softmax_loss(x, y)
# Test softmax_loss function. Loss should be close to 2.3 and dx error should be around e-8
print('\nTesting softmax_loss:')
print('loss: ', loss)
print('dx error: ', rel_error(dx_num, dx))Two-layer network
np.random.seed(231)
N, D, H, C = 3, 5, 50, 7
X = np.random.randn(N, D)
y = np.random.randint(C, size=N)
std = 1e-3
model = TwoLayerNet(input_dim=D, hidden_dim=H, num_classes=C, weight_scale=std)
print('Testing initialization ... ')
W1_std = abs(model.params['W1'].std() - std)
b1 = model.params['b1']
W2_std = abs(model.params['W2'].std() - std)
b2 = model.params['b2']
assert W1_std < std / 10, 'First layer weights do not seem right'
assert np.all(b1 == 0), 'First layer biases do not seem right'
assert W2_std < std / 10, 'Second layer weights do not seem right'
assert np.all(b2 == 0), 'Second layer biases do not seem right'
print('Testing test-time forward pass ... ')
model.params['W1'] = np.linspace(-0.7, 0.3, num=D*H).reshape(D, H)
model.params['b1'] = np.linspace(-0.1, 0.9, num=H)
model.params['W2'] = np.linspace(-0.3, 0.4, num=H*C).reshape(H, C)
model.params['b2'] = np.linspace(-0.9, 0.1, num=C)
X = np.linspace(-5.5, 4.5, num=N*D).reshape(D, N).T
scores = model.loss(X)
correct_scores = np.asarray(
[[11.53165108, 12.2917344, 13.05181771, 13.81190102, 14.57198434, 15.33206765, 16.09215096],
[12.05769098, 12.74614105, 13.43459113, 14.1230412, 14.81149128, 15.49994135, 16.18839143],
[12.58373087, 13.20054771, 13.81736455, 14.43418138, 15.05099822, 15.66781506, 16.2846319 ]])
scores_diff = np.abs(scores - correct_scores).sum()
assert scores_diff < 1e-6, 'Problem with test-time forward pass'
print('Testing training loss (no regularization)')
y = np.asarray([0, 5, 1])
loss, grads = model.loss(X, y)
correct_loss = 3.4702243556
assert abs(loss - correct_loss) < 1e-10, 'Problem with training-time loss'
model.reg = 1.0
loss, grads = model.loss(X, y)
correct_loss = 26.5948426952
assert abs(loss - correct_loss) < 1e-10, 'Problem with regularization loss'
# Errors should be around e-7 or less
for reg in [0.0, 0.7]:
print('Running numeric gradient check with reg = ', reg)
model.reg = reg
loss, grads = model.loss(X, y)
for name in sorted(grads):
f = lambda _: model.loss(X, y)[0]
grad_num = eval_numerical_gradient(f, model.params[name], verbose=False)
print('%s relative error: %.2e' % (name, rel_error(grad_num, grads[name])))model 实现
class TwoLayerNet(object):
def __init__(self, input_dim=3*32*32, hidden_dim=50, num_classes=10,
weight_scale=1e-3, reg=0.8):
self.params = {}
self.reg = reg
############################################################################
# TODO: Initialize the weights and biases of the two-layer net. Weights #
# should be initialized from a Gaussian centered at 0.0 with #
# standard deviation equal to weight_scale, and biases should be #
# initialized to zero. All weights and biases should be stored in the #
# dictionary self.params, with first layer weights #
# and biases using the keys 'W1' and 'b1' and second layer #
# weights and biases using the keys 'W2' and 'b2'. #
############################################################################
self.params['W1'] = weight_scale * np.random.randn(input_dim, hidden_dim)
self.params['b1'] = np.zeros(hidden_dim)
self.params['W2'] = weight_scale * np.random.randn(hidden_dim, num_classes)
self.params['b2'] = np.zeros(num_classes)
############################################################################
# END OF YOUR CODE #
############################################################################
def loss(self, X, y=None):
"""
Compute loss and gradient for a minibatch of data.
Inputs:
- X: Array of input data of shape (N, d_1, ..., d_k)
- y: Array of labels, of shape (N,). y[i] gives the label for X[i].
Returns:
If y is None, then run a test-time forward pass of the model and return:
- scores: Array of shape (N, C) giving classification scores, where
scores[i, c] is the classification score for X[i] and class c.
If y is not None, then run a training-time forward and backward pass and
return a tuple of:
- loss: Scalar value giving the loss
- grads: Dictionary with the same keys as self.params, mapping parameter
names to gradients of the loss with respect to those parameters.
"""
scores = None
############################################################################
# TODO: Implement the forward pass for the two-layer net, computing the #
# class scores for X and storing them in the scores variable. #
############################################################################
# Unpack variables from the params dictionary
W1, b1 = self.params['W1'], self.params['b1']
W2, b2 = self.params['W2'], self.params['b2']
X = X.reshape(X.shape[0], -1)
# 计算分值
h1_out,h1_cache = affine_relu_forward(X, W1, b1)
scores,out_cache = affine_forward(h1_out, W2, b2)
#############################################################################
# END OF YOUR CODE #
#############################################################################
# If the targets are not given then jump out, we're done
if y is None:
return scores
# Compute the loss
loss = None
#############################################################################
# TODO: Finish the forward pass, and compute the loss. This should include #
# both the data loss and L2 regularization for W1 and W2. Store the result #
# in the variable loss, which should be a scalar. Use the Softmax #
# classifier loss. #
#############################################################################
# 最后一层softmax
loss,dout = softmax_loss(scores,y)
loss += 0.5 * self.reg * (np.sum(W1 ** 2) + np.sum(W2 ** 2))
#############################################################################
# END OF YOUR CODE #
#############################################################################
# Backward pass: compute gradients
grads = {}
#############################################################################
# TODO: Compute the backward pass, computing the derivatives of the weights #
# and biases. Store the results in the grads dictionary. For example, #
# grads['W1'] should store the gradient on W1, and be a matrix of same size #
#############################################################################
# 计算梯度
dout, dw2, db2 = affine_backward(dout, out_cache)
dw2 += self.reg * W2
grads['W2'] = dw2
grads['b2'] = db2
_, dw1, db1 = affine_relu_backward(dout, h1_cache)
dw1 += self.reg * W1
grads['W1'] = dw1
grads['b1'] = db1
#############################################################################
# END OF YOUR CODE #
#############################################################################
return loss, grads- 模型实现后,开始导入真实数据并训练
data = get_CIFAR10_data()
for k, v in list(data.items()):
print(('%s: ' % k, v.shape))
model = TwoLayerNet()
solver = None
##############################################################################
# TODO: Use a Solver instance to train a TwoLayerNet that achieves at least #
# 50% accuracy on the validation set. #
##############################################################################
data_mini = {}
for k, v in data.items():
N = int(v.shape[0] / 5)
data_mini[k] = data[k][:N]
print(k, N)
solver = Solver(model, data,
num_train_samples=1000,
lr_decay=0.95,
num_epochs=20,
batch_size=200,
optim_config={
'learning_rate': 1e-3,
}
)
solver.train()
##############################################################################
# END OF YOUR CODE #
##############################################################################
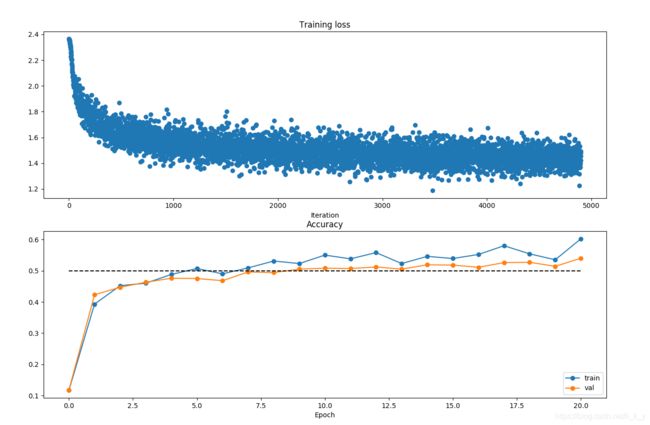
- 画出 loss 和 acc
# Run this cell to visualize training loss and train / val accuracy
plt.subplot(2, 1, 1)
plt.title('Training loss')
plt.plot(solver.loss_history, 'o')
plt.xlabel('Iteration')
plt.subplot(2, 1, 2)
plt.title('Accuracy')
plt.plot(solver.train_acc_history, '-o', label='train')
plt.plot(solver.val_acc_history, '-o', label='val')
plt.plot([0.5] * len(solver.val_acc_history), 'k--')
plt.xlabel('Epoch')
plt.legend(loc='lower right')
plt.gcf().set_size_inches(15, 12)
plt.show()
多层网络的实现
Multilayer network
class FullyConnectedNet(object):
def __init__(self, hidden_dims, input_dim=3*32*32, num_classes=10,
dropout=1, normalization=None, reg=0.0,
weight_scale=1e-2, dtype=np.float32, seed=None):
self.normalization = normalization
self.use_dropout = dropout != 1
self.reg = reg
self.num_layers = 1 + len(hidden_dims)
self.dtype = dtype
self.params = {}
############################################################################
# TODO: Initialize the parameters of the network, storing all values in #
# the self.params dictionary. Store weights and biases for the first layer #
# in W1 and b1; for the second layer use W2 and b2, etc. Weights should be #
# initialized from a normal distribution centered at 0 with standard #
# deviation equal to weight_scale. Biases should be initialized to zero. #
# #
# When using batch normalization, store scale and shift parameters for the #
# first layer in gamma1 and beta1; for the second layer use gamma2 and #
# beta2, etc. Scale parameters should be initialized to ones and shift #
# parameters should be initialized to zeros. #
############################################################################
in_dim = input_dim
for i, h_dim in enumerate(hidden_dims):
self.params['W%d' %(i+1,)] = weight_scale * np.random.randn(in_dim, h_dim)
self.params['b%d' %(i+1,)] = np.zeros((h_dim,))
if self.normalization=='batchnorm':
self.params['gamma%d' %(i+1,)] = np.ones((h_dim,))
self.params['bets%d' %(i+1,)] = np.zeros((h_dim,))
in_dim = h_dim
self.params['W%d' %(self.num_layers,)] = weight_scale * np.random.randn(in_dim, num_classes)
self.params['b%d' %(self.num_layers,)] = np.zeros((num_classes,))
############################################################################
# END OF YOUR CODE #
############################################################################
# When using dropout we need to pass a dropout_param dictionary to each
# dropout layer so that the layer knows the dropout probability and the mode
# (train / test). You can pass the same dropout_param to each dropout layer.
self.dropout_param = {}
if self.use_dropout:
self.dropout_param = {'mode': 'train', 'p': dropout}
if seed is not None:
self.dropout_param['seed'] = seed
# With batch normalization we need to keep track of running means and
# variances, so we need to pass a special bn_param object to each batch
# normalization layer. You should pass self.bn_params[0] to the forward pass
# of the first batch normalization layer, self.bn_params[1] to the forward
# pass of the second batch normalization layer, etc.
self.bn_params = []
if self.normalization=='batchnorm':
self.bn_params = [{'mode': 'train'} for i in range(self.num_layers - 1)]
if self.normalization=='layernorm':
self.bn_params = [{} for i in range(self.num_layers - 1)]
# Cast all parameters to the correct datatype
for k, v in self.params.items():
self.params[k] = v.astype(dtype)
def loss(self, X, y=None):
"""
Compute loss and gradient for the fully-connected net.
Input / output: Same as TwoLayerNet above.
"""
X = X.astype(self.dtype)
mode = 'test' if y is None else 'train'
# Set train/test mode for batchnorm params and dropout param since they
# behave differently during training and testing.
if self.use_dropout:
self.dropout_param['mode'] = mode
if self.normalization=='batchnorm':
for bn_param in self.bn_params:
bn_param['mode'] = mode
scores = None
############################################################################
# TODO: Implement the forward pass for the fully-connected net, computing #
# the class scores for X and storing them in the scores variable. #
# #
# When using dropout, you'll need to pass self.dropout_param to each #
# dropout forward pass. #
# #
# When using batch normalization, you'll need to pass self.bn_params[0] to #
# the forward pass for the first batch normalization layer, pass #
# self.bn_params[1] to the forward pass for the second batch normalization #
# layer, etc. #
############################################################################
fc_mix_cache = {}
if self.use_dropout:
dp_cache = {}
# 循环每一个hidden layer
out = X
for i in range(self.num_layers - 1):
w, b = self.params['W%d' %(i+1,)], self.params['b%d' %(i+1,)]
if self.normalization=='batchnorm':
gamma = self.params['gamma%d' %(i+1,)]
beta = self.params['beta%d' %(i+1,)]
out, fc_mix_cache[i] = affine_bn_relu_forward(out, w, b, gamma, beta, self.bn_params[i])
else:
out, fc_mix_cache[i] = affine_relu_forward(out, w, b)
if self.use_dropout:
out, dp_cache[i] = dropout_forward(out, self.dropout_param)
# 最后一层
w = self.params['W%d' %(self.num_layers,)]
b = self.params['b%d' %(self.num_layers,)]
out, out_cache = affine_forward(out, w, b)
scores = out
############################################################################
# END OF YOUR CODE #
############################################################################
# If test mode return early
if mode == 'test':
return scores
loss, grads = 0.0, {}
############################################################################
# TODO: Implement the backward pass for the fully-connected net. Store the #
# loss in the loss variable and gradients in the grads dictionary. Compute #
# data loss using softmax, and make sure that grads[k] holds the gradients #
# for self.params[k]. Don't forget to add L2 regularization! #
# #
# When using batch/layer normalization, you don't need to regularize the scale #
# and shift parameters. #
# #
# NOTE: To ensure that your implementation matches ours and you pass the #
# automated tests, make sure that your L2 regularization includes a factor #
# of 0.5 to simplify the expression for the gradient. #
############################################################################
loss, dout = softmax_loss(scores, y)
loss += 0.5 * self.reg * np.sum(self.params['W%d' %(self.num_layers,)] ** 2)
dout, dw, db = affine_backward(dout, out_cache)
grads['W%d' %(self.num_layers,)] = dw + self.reg * self.params['W%d' %(self.num_layers,)]
grads['b%d' %(self.num_layers,)] = db
# 在每一个隐藏层处梯度反向传播
for i in range(self.num_layers - 1):
ri = self.num_layers - 2 - i
loss += 0.5 * self.reg * np.sum(self.params['W%d' %(ri+1,)] ** 2)
if self.use_dropout:
dout = dropout_backward(dout, dp_cache[ri])
if self.normalization=='batchnorm':
dout, dw, db, dgamma, dbeta = affine_bn_relu_forward(dout, fc_mix_cache[ri])
grads['gamma%d' %(ri+1,)] = dgamma
grads['beta%d' %(ri+1,)] = dbeta
else:
dout, dw, db = affine_relu_backward(dout, fc_mix_cache[ri])
grads['W%d' %(ri+1,)] = dw + self.reg * self.params['W%d' %(ri+1,)]
grads['b%d' %(ri+1,)] = db
############################################################################
# END OF YOUR CODE #
############################################################################
return loss, gradsFirst we will try a three-layer network with 100 units in each hidden layer. In the following cell, tweak the learning rate and initialization scale to overfit and achieve 100% training accuracy within 20 epochs.
num_train = 50
small_data = {
'X_train': data['X_train'][:num_train],
'y_train': data['y_train'][:num_train],
'X_val': data['X_val'],
'y_val': data['y_val'],
}
learning_rate = 1e-2
weight_scale = 1e-2
model = FullyConnectedNet([100, 100],
weight_scale=weight_scale, dtype=np.float64)
solver = Solver(model, small_data,
print_every=1, num_epochs=20, batch_size=25,
update_rule='sgd',
optim_config={
'learning_rate': learning_rate,
}
)
solver.train()
plt.subplot(2, 1, 1)
plt.plot(solver.loss_history, 'o')
plt.title('Training loss history')
plt.xlabel('Iteration')
plt.ylabel('Training loss')
plt.subplot(2, 1, 2)
plt.title('Accuracy')
plt.plot(solver.train_acc_history, '-o', label='train')
plt.plot(solver.val_acc_history, '-o', label='val')
plt.plot([0.5] * len(solver.val_acc_history), 'k--')
plt.xlabel('Epoch')
plt.legend(loc='lower right')
plt.gcf().set_size_inches(15, 12)
plt.show()
plt.show()
Now try to use a five-layer network with 100 units on each layer to overfit 50 training examples. Again you will have to adjust the learning rate and weight initialization, but you should be able to achieve 100% training accuracy within 20 epochs.
learning_rate = 1e-2
weight_scale = 5e-2
model = FullyConnectedNet([100, 100, 100, 100],
weight_scale=weight_scale, dtype=np.float64)
solver = Solver(model, small_data,
print_every=1, num_epochs=20, batch_size=25,
update_rule='sgd',
optim_config={
'learning_rate': learning_rate,
}
)
solver.train()
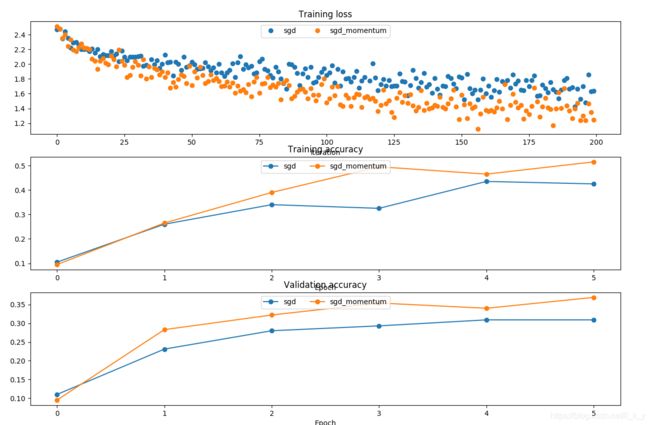
SGD+Momentum
实现:
def sgd_momentum(w, dw, config=None):
"""
Performs stochastic gradient descent with momentum.
config format:
- learning_rate: Scalar learning rate.
- momentum: Scalar between 0 and 1 giving the momentum value.
Setting momentum = 0 reduces to sgd.
- velocity: A numpy array of the same shape as w and dw used to store a
moving average of the gradients.
"""
if config is None: config = {}
config.setdefault('learning_rate', 1e-2)
config.setdefault('momentum', 0.9)
v = config.get('velocity', np.zeros_like(w))
next_w = None
###########################################################################
# TODO: Implement the momentum update formula. Store the updated value in #
# the next_w variable. You should also use and update the velocity v. #
###########################################################################
v = config['momentum'] * v - config['learning_rate'] * dw
next_w = w + v
###########################################################################
# END OF YOUR CODE #
###########################################################################
config['velocity'] = v
return next_w, config
RMSProp and Adam
RMSProp 实现:
def rmsprop(w, dw, config=None):
if config is None: config = {}
config.setdefault('learning_rate', 1e-2)
config.setdefault('decay_rate', 0.99)
config.setdefault('epsilon', 1e-8)
config.setdefault('cache', np.zeros_like(w))
next_w = None
###########################################################################
# TODO: Implement the RMSprop update formula, storing the next value of w #
# in the next_w variable. Don't forget to update cache value stored in #
# config['cache']. #
###########################################################################
config['cache'] = config['decay_rate'] * config['cache'] + (1 - config['decay_rate']) * dw * dw
next_w = w - config['learning_rate'] * dw / (np.sqrt(config['cache']) + config['epsilon'])
###########################################################################
# END OF YOUR CODE #
###########################################################################
return next_w, config
Adam 实现:
def adam(w, dw, config=None):
if config is None: config = {}
config.setdefault('learning_rate', 1e-3)
config.setdefault('beta1', 0.9)
config.setdefault('beta2', 0.999)
config.setdefault('epsilon', 1e-8)
config.setdefault('m', np.zeros_like(w))
config.setdefault('v', np.zeros_like(w))
config.setdefault('t', 0)
next_w = None
###########################################################################
# TODO: Implement the Adam update formula, storing the next value of w in #
# the next_w variable. Don't forget to update the m, v, and t variables #
# stored in config. #
# #
# NOTE: In order to match the reference output, please modify t _before_ #
# using it in any calculations. #
###########################################################################
config['m'] = config['beta1'] * config['m'] + (1 - config['beta1']) * dw
config['v'] = config['beta2'] * config['v'] + (1 - config['beta2']) * dw * dw
# first_bias = config['m'] / (1 - config['beta1'] ** config['t'])
# second_bias = config['v'] / (1 - config['beta2'] ** config['t'])
# next_w = w - config['learning_rate'] * first_bias / (np.sqrt(second_bias) + config['epsilon'])
next_w = w - config['learning_rate'] * config['m'] / (np.sqrt(config['v']) + config['epsilon'])
###########################################################################
# END OF YOUR CODE #
###########################################################################
return next_w, confignum_train = 4000
small_data = {
'X_train': data['X_train'][:num_train],
'y_train': data['y_train'][:num_train],
'X_val': data['X_val'],
'y_val': data['y_val'],
}
solvers = {}
learning_rates = {'rmsprop': 1e-4, 'adam': 1e-3}
for update_rule in ['adam', 'rmsprop']:
print('running with ', update_rule)
model = FullyConnectedNet([100, 100, 100, 100], weight_scale=5e-2)
solver = Solver(model, small_data,
num_epochs=5, batch_size=100,
update_rule=update_rule,
optim_config={
'learning_rate': learning_rates[update_rule]
},
verbose=True)
solvers[update_rule] = solver
solver.train()
print()
plt.subplot(3, 1, 1)
plt.title('Training loss')
plt.xlabel('Iteration')
plt.subplot(3, 1, 2)
plt.title('Training accuracy')
plt.xlabel('Epoch')
plt.subplot(3, 1, 3)
plt.title('Validation accuracy')
plt.xlabel('Epoch')
for update_rule, solver in list(solvers.items()):
plt.subplot(3, 1, 1)
plt.plot(solver.loss_history, 'o', label=update_rule)
plt.subplot(3, 1, 2)
plt.plot(solver.train_acc_history, '-o', label=update_rule)
plt.subplot(3, 1, 3)
plt.plot(solver.val_acc_history, '-o', label=update_rule)
for i in [1, 2, 3]:
plt.subplot(3, 1, i)
plt.legend(loc='upper center', ncol=4)
plt.gcf().set_size_inches(15, 15)
plt.show()Train a good model
Train the best fully-connected model that you can on CIFAR-10, storing your best model in the best_model variable. We require you to get at least 50% accuracy on the validation set using a fully-connected net.
num_train = 20000
small_data = {
'X_train': data['X_train'][:num_train],
'y_train': data['y_train'][:num_train],
'X_val': data['X_val'],
'y_val': data['y_val'],
}
best_model = None
################################################################################
# TODO: Train the best FullyConnectedNet that you can on CIFAR-10. You might #
# find batch/layer normalization and dropout useful. Store your best model in #
# the best_model variable. #
################################################################################
# find the best nn
best_val = -1
results = {}
learning_rates = [2e-4, 3e-4]
regularization_strengths = [7e-2, 8e-2, 9e-2]
# np.linspace(1e-3, 1e0, num=15)
# lr: 0.0002 reg: 0.089 train acc: 0.5175 val_acc: 0.418
# lr: 0.0002 reg: 0.0723571428571 train acc: 0.4915 val_acc: 0.409
# learning_rates = np.linspace(1e-4, 1e-3, num=10)
for lr in learning_rates:
for rg in regularization_strengths:
solvers = {}
model = FullyConnectedNet([100, 100, 100, 100], weight_scale=5e-2, reg=rg)
solver = Solver(model, small_data,
num_epochs=20, batch_size=100,
update_rule='adam',
optim_config={
'learning_rate': lr
},
verbose=False)
solver.train()
y_train_pred = np.argmax(model.loss(small_data['X_train']), axis=1)
acc_train = np.mean(y_train_pred == small_data['y_train'])
y_val_pred = np.argmax(model.loss(small_data['X_val']), axis=1)
acc_val = np.mean(y_val_pred == small_data['y_val'])
results[(lr, rg)] = (acc_train, acc_val)
if best_val < acc_val:
best_val = acc_val
best_model = model
for lr, rg in results:
train_acc, val_acc = results[(lr, rg)]
print('lr: ', lr, 'reg: ', rg, ' train acc: ', train_acc, ' val_acc: ', val_acc)
################################################################################
# END OF YOUR CODE #
################################################################################
y_test_pred = np.argmax(best_model.loss(data['X_test']), axis=1)
y_val_pred = np.argmax(best_model.loss(data['X_val']), axis=1)
print('Validation set accuracy: ', (y_val_pred == data['y_val']).mean())
print('Test set accuracy: ', (y_test_pred == data['y_test']).mean())