MNIST的四种写法
MNIST是什么
MNIST是一组经过预处理的手写数字图片数据集,它为机器学习的初学者提供了一个练手的机会,可以在真实的数据上用学到的算法来解决问题。由于很多的机器学习教程都以MNIST作为入门项目,因此它也被称作是机器学习领域的“hello world”。
MNIST中每个样本都是一张长28、宽28的灰度图片,其中包含一个0-9的数字。我们需要做的,就是根据训练数据建立一个模型用来识别输入图片中的数字。这是典型的分类问题,每个样本的输入是784维向量:一张图片有28*28=784个像素点,每个点用一个浮点数表示其亮度;输出是10维向量,十个分量分别表示输入图中数字是0~9的可能性,其中可能性最大的,就是算法预测的结果。
准备工作
本文的代码采用Python和TensorFlow编写,所以需要一个Python开发环境,2.7或者3.0都可以。很多开源软件和库对Windows的支持都不是很好,建议使用Linux或者Mac OS X,可以避免很多不必要的麻烦。推荐使用pip安装TensorFlow:
pip install tensorflow
如果有一块支持CUDA的显卡,就可以安装TensorFlow的GPU版本。使用GPU计算会大大缩短模型的训练时间:
pip install tensorflow-gpu
安装问题可以参考TensorFlow的官方文档或者pip的主页,这里不再赘述。
框架
在开始具体的算法之前,我们先搭建一个通用的框架。框架要完成一些不同算法都需要做的工作,比如加载数据集、定义和训练模型,验证模型准确率等等。这样后面实现具体算法的时候就只需要关注跟算法相关的代码。下面是框架的代码,具体的解释已经放在注释里了,[...]的部分就是在各种算法中需要实现的部分。
# encoding: utf-8
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
# 模型参数,需要声明为tensorflow变量(tf.Variable)
[...]
# 预测函数,根据输入和模型参数计算输出结果。这个函数定义了算法模型,
# 不同算法的区别主要就在这里
def inference(x):
[...]
# 损失函数(cost function),不同算法会使用不同的损失函数,但在这篇
# 文章里都是调用tf提供的库函数,因而区别不大
def loss(x, y):
[...]
# 训练数据,这里使用TensorFlow的占位符机制,其作用类似于函数的形参
X = tf.placeholder(tf.float32, [None, 784])
y_ = tf.placeholder(tf.float32, [None, 10])
z = inference(X)
total_loss = loss(X, y_)
# 学习速率,取值过大可能导致算法不能收敛。不同算法可能需要使用的不同值
learning_rate = 0.5
# 使用梯度下降算法寻找损失函数的极小值
train_op = tf.train.GradientDescentOptimizer(learning_rate).minimize(total_loss)
# 验证预测的准确率
correct_prediction = tf.equal(tf.argmax(z, 1), tf.argmax(y_, 1))
evaluate = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
# 读取数据集,这里tf已经封装好了
mnist = input_data.read_data_sets("./data", one_hot=True)
# 把loss作为scalar summary写到tf的日志,这样就可以通过tensorboard
# 查看损失函数的变化情况,进行算法调试
writer = tf.summary.FileWriter("./log", graph=tf.get_default_graph())
loss_summary = tf.summary.scalar(b'Loss', total_loss)
with tf.Session() as sess:
# 初始化TensorFlow变量,也就是模型参数
sess.run(tf.global_variables_initializer())
# 训练模型
training_steps = 10000
batch_size = 100
for step in range(training_steps):
batch_xs, batch_ys = mnist.train.next_batch(batch_size)
placeholder_dict = {X: batch_xs, y_: batch_ys}
sess.run(train_op, feed_dict=placeholder_dict)
summary = sess.run(loss_summary, feed_dict=placeholder_dict)
writer.add_summary(summary, global_step=step)
#在测试集上验证模型准确率
print sess.run(evaluate,
feed_dict={X: mnist.test.images,
y_: mnist.test.labels})
机器学习的过程,就是用模型对训练数据进行拟合的过程。这里有两个核心,其一是“模型”。一个机器学习模型应该包括两个部分:从输入到输出的计算过程,也就是框架里的inference()函数;以及计算模型拟合程度的损失函数,也就是loss()函数。本文中的几种算法,还有其他更复杂的机器学习算法,都是一些经过验证具有实用价值的模型。机器学习算法的第二个关键是“拟合”,也就是在给定的模型和训练数据下,寻找损失函数的极小值。拿人类类比一下,“模型”决定了我们如何利用已有的经验做出决策,而“拟合”决定了我们如何根据决策的结果学习新的经验。不同机器学习算法的模型千差万别,但是拟合的过程都是类似的。在这篇文章里,我们用到的是最基础的批量梯度下降算法(Batch Gradient Descent),TensorFlow已经帮我们实现了该算法,因此我们要做的就是定义好模型,提供模型参数和inference()和loss()两个函数,然后使用GradientDescentOptimizer就可以完成拟合的过程。TensorFlow还提供了其他最优化算法,可以参考这里。
框架代码里用到了TensorFlow的summary,其作用是把变量的值记录在日志里,这样就可以通过日志跟踪某个变量在模型运算过程中的变化情况,比如这里用来跟踪损失函数。程序运行结束之后,可以用TensorBoard查看:
tensorboard --logdir=./log/
其中./log就是FileWriter()中指定的日志目录。执行命令之后按照提示在浏览器中打开http://127.0.0.1:6006, 在“SCALARS”标签页中就能看到loss变量的变化曲线。跟踪损失函数的值在调试机器学习代码时是很有用的。在模型和代码都正确的情况下,损失函数应该是逐渐减小的,否则就是代码有问题,可能是模型问题,代码实现不对,或者学习速率(learning_rate)过大导致损失函数无法收敛。
算法1:Logistic回归
Logistic回归是一种简单的二元分类算法,其核心是sigmoid函数,其函数定义如下:
Sigmoid函数接受一个实数作为输入参数,输出为(0, 1)区间内的一个数值。这个输出值可以被当作某件事发生的概率。具体到分类问题,我们可以在输出值大于等于0.5时预测该样本为正例,否则预测为反例。0.5这个阈值并非固定的,可以根据实际情况进行调整,选择预测效果最佳的。对于MNIST问题,要使用Logistic回归进行识别,首先要把输入的784维特征向量转化为一个标量,这可以通过线性函数来实现:
或者写成向量形式:
![]()
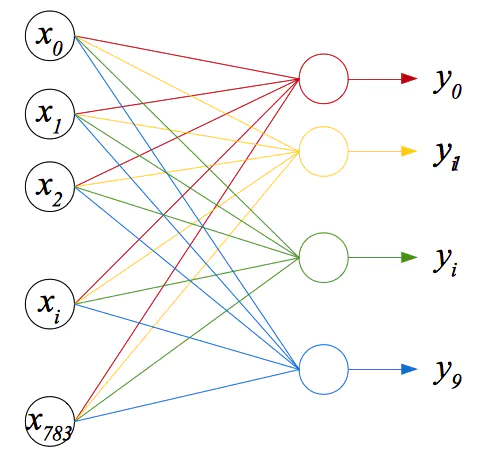
接下来,只要把线性函数的输出作为sigmoid函数的输入,就可以得到一个概率值。由于sigmoid函数本身是没有可变参数的,因此模型的输出主要取决与第一步的线性函数的参数W和b。Logistic回归的模型有了,但是并没有解决数字识别的问题。Logistic回归是二元分类算法,只能回答“是”和“否”的问题,而MNIST问题有10种不同的可能。一种直接的思路是:训练10个不同的分类器,分别对应10个数字,这种方法叫做“one-vs-all”。图1就是用这种方法构建的手写数字识别器示意图。这个图后面还会提到。
图1:用one-vs-all方法构建的Logistic分类器
Logistic回归算法对应的代码如下:
# 模型参数,一个分类器的W是784维向量,10个分类器就是784*10的矩阵
W = tf.Variable(tf.zeros([784, 10]))
b = tf.Variable(tf.zeros([10]))
# 预测函数
def inference(x):
z = tf.matmul(X, W) + b
# 返回预测结果,这里没有计算sigmoid的原因是:
# 1. 损失函数需要用到z
# 2. sigmoid函数是单调递增的,因此这里z越大,sigmoid的输出也越大。
# 所以只根据z就可以确定预测结果,不必再计算sigmoid。
return z
# 损失函数,这里使用交叉熵(cross entropy)
def loss(x, y):
z = inference(x)
return tf.reduce_mean(
tf.nn.sigmoid_cross_entropy_with_logits(
logits=z, labels=y))
算法2:Softmax回归
尽管Logistic回归可以通过“one-vs-all”方法解决多标签分类问题,但是这个结果还是有一点不符合常识:假定输入图片是一个数字的情况下,那么它必定是0-9这10个数字中的一个,算法输出的10个概率之和应该正好为1。上一节的方法并不能保证这一点,而本节使用Softmax回归算法可以。
Softmax回归的核心是Softmax函数。该函数接受n个实数输入,并输出n个[0, 1]区间内的数值,第i个输出的值为:
Softmax函数的n个输出之和为1,正好可以用来建立多标签分类的模型。要使用Softmax函数来建立MNIST的分类模型,首先要把输入的784维特征向量转换成10个特征值,这个工作我们在上一节就已经完成了。这里我们使用相同的方法:10个线性函数。接下来只要把10个特征值输入Softmax函数即可。这个模型跟“one-vs-all”的Logistic回归模型如出一辙,唯一的区别是sigmoid函数换成了softmax函数。反映在代码实现上,只是在计算损失函数时用softmax_cross_entropy_with_logits()替换了sigmoid_cross_entropy_with_logits()。
# 模型参数
W = tf.Variable(tf.zeros([784, 10]))
b = tf.Variable(tf.zeros([10]))
# 预测函数
def inference(x):
# 这里也只计算了线性函数的输出而没有计算softmax,
# 原因跟logistic回归是一样的
z = tf.matmul(X, W) + b
return z
# 损失函数
def loss(x, y):
z = inference(x)
return tf.reduce_mean(
tf.nn.softmax_cross_entropy_with_logits(
logits=z, labels=y))
算法3:神经网络
神经网络是通过模拟人的神经系统来实现机器学习的一类算法,也是深度学习的基础。神经网络中的每个单元(也称作“神经元”)接受n个实数输入,加权求和之后,再经过一个激活函数计算得到一个输出。多个神经元并联形成一个层,多个层串联就形成了一个神经网络。
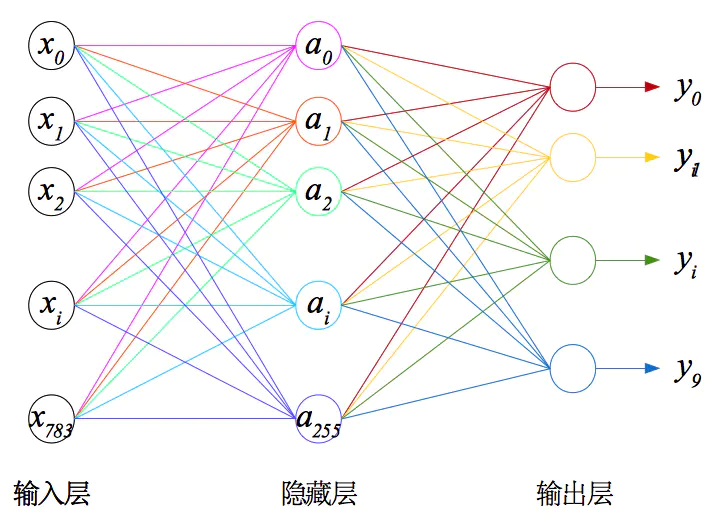
看过神经网络的描述,是不是觉得有点眼熟?回顾一下前面的Logistic回归算法,Logistic分类器是不是跟这里的神经元差不多?如果使用sigmoid函数作为激活函数,一个神经元就是一个logistic分类器。事实上,sigmoid函数也确实是常用的激活函数之一,也是我们这里要使用的激活函数。其他常用激活函数还有tanh和ReLU。再看图1中用“one-vs-all”方式构建的多标签分类器,也基本符合神经网络的定义。不过它还不能算是一个合格的神经网络。一个神经网络至少应该有三层:输入层、隐藏层和输出层。图1只有输入层和输出层,缺少一个隐藏层。图2就是本节要使用的神经网络,也是最简单的三层神经网络。
图2:三层神经网络
虽然只是多了一个隐藏层而已,但是在很多应用场景中效果已经相当不错。比如CMU在上世纪80年代开发的ALVINN系统,只用了最简单的三层神经网络就实现了自动驾驶,效果可以看这里。不能上YouTube的可以看参考资料1,里面也有这段演示。不过神经网络的缺点也很明显,就是计算量大。神经网络的损失函数是所有层的损失函数之和,而训练过程也要更新所有层的权值。训练神经网络的算法称作反向传播算法(BP,Backpropagation)。简单来说,BP就是先计算输出层的梯度,然后逐层反推,计算出所有隐藏层的梯度,然后根据这些梯度去更新权值。网络层次越多,每层单元数量越多,计算量也就越大。如果不是GPU计算的出现大大缩短了神经网络的训练时间,深度学习现在也不会这么火爆。TensorFlow以及其他主流机器学习框架中都已经实现了BP算法,因此不需要我们关注这些细节。关于BP算法的推导和实现,有兴趣可以去看参考资料1。本人水平有限,这里就不献丑了。
下面是用神经网络来解决MNIST问题的代码:
# 模型参数
num_of_hidden_units = 256 # 隐藏层单元数
# 隐藏层,使用sigmoid激活函数
# 权值不能初始化为0,否则训练过程中权值的所有分量都会一直保持相同的值
W1 = tf.Variable(tf.truncated_normal([784, num_of_hidden_units]))
b1 = tf.Variable(tf.zeros([num_of_hidden_units]))
# softmax输出层
# 权值不能初始化为0,否则训练过程中权值的所有分量都会一直保持相同的值
W2 = tf.Variable(tf.truncated_normal([num_of_hidden_units, 10]))
b2 = tf.Variable(tf.zeros([10]))
# 预测函数,算法的核心
def inference(x):
# 隐藏层
z1 = tf.matmul(X, W1) + b1
a1 = tf.sigmoid(z1)
# 输出层,softmax函数不用计算
z2 = tf.matmul(a1, W2) + b2
return z2
# 损失函数(cost function)
def loss(x, y):
z = inference(x)
return tf.reduce_mean(
tf.nn.softmax_cross_entropy_with_logits(
logits=z, labels=y))
算法4:卷积神经网络
卷积神经网络(Convolutional Neural Network, CNN)是出现比较早也比较成熟的深度学习算法之一,主要应用与图像识别问题,例如本文的MNIST。简单来说,CNN就是具有至少一个卷积层的神经网络。这里的卷积,是指离散卷积,其定义如下:
其中f是输入图像,g称作核函数(kernal function)。卷积层的作用是对图像进行特征提取,不同的核函数可以提取出图像不同方面的特征。用传统的机器学习方法进行图像识别,需要使用专门的图像处理算法预先将原始图像转换成某种特征向量,才能进行模型训练。提取特征的质量直接关系到最后的结果。用CNN就没有这些麻烦,可以直接用原始图像训练模型,这也是CNN(以及其他深度学习算法)受热捧的原因之一。
数学不好,对卷积运算就不再纠缠了,TensorFlow中有现成的函数conv2d(),知道怎么调用就可以了。在本节的实现中,W_conv就是核函数,[5, 5, 1, 64]表示这个核函数可以对长为5、宽为5、通道数为1的图像进行运算,输出5*5*64的张量。通道数是指每个像素点用多少个数值表示。MNIST使用的是灰度图像,每个像素点只需要一个数值,因此这里通道数为1。如果是RGB图像,就需要三个数值,通道数就是3。
函数conv2d()就是把输入图像分成若干个5*5的小块,逐个与核函数进行运算,然后输出结果。参数padding表示进行卷积运算时对原始图像的分块方式,SAME表示输出的尺寸与输入图像的长宽保持一致,因此在本例中conv2d()的输出就是28*\28*64。按照这种分块方式,输入图像的边缘区域就没有足够多的像素进行卷积运算,算法会用0填充(也就是padding)之后再进行卷积。参数padding的另一种取值是VALID,表示不对原始图像进行填充,卷积运算只会覆盖到输入图像的有效像素。如果使用VALID方式,这里的输出就变成了24*\24*64,隐藏层对应的参数也要相应的进行修改,有兴趣可以试一下。
卷积层同样需要一个激活函数,这里使用前面提到过的ReLU函数,定义如下:
卷积运算通常会增加每个样本数据点的数量,比如这里就把28*28*1的输入图像变成了28*28*64个特征值。这大大增加了模型的运算量。因此,卷积层之后通常紧随一个pooling层,用来进行下降抽样(down sampling),加快运算速度。它把输入图像分割成指定大小的矩形区域,输出每个区域内点的最大值(max-pooling)或平均值(mean-pooling)。本文的代码中使用TensorFlow提供的max_pool()函数。参数ksize表示抽样的尺寸,四个数值分别表示batch、height、width、channels,[1, 4, 4, 1]的含义就是每次对1个输入样本中4*4区域的1个通道进行抽样。参数strides表示多次抽样之间的间隔距离,strides和ksize的情况下,多次抽样之间就不会有交叉。因此,这里做的就是对卷积输出中每个不相交的4*4区域的每个通道分别取最大值,得到的输出为7*7*64的张量。参数padding的含义与conv2d()相同。
到这里,用卷积运算进行特征提取已经完成了。对于更复杂的应用,可能有多个卷积层,这里就不讨论了。在本文的实现中,pooling层之后就是和第3节中一样的全连接隐藏层,不过这里使用ReLU替代sigmoid作为激活函数。最后再使用一个第2节中的softmax层作为输出层。代码如下:
# 卷积层,W_conv即核函数
W_conv = tf.Variable(tf.truncated_normal([5, 5, 1, 64]))
b_conv = tf.Variable(tf.zeros([64]))
# 全连接隐藏层
W_hidden = tf.Variable(tf.truncated_normal([7 * 7 * 64, 1024]))
b_hidden = tf.Variable(tf.zeros([1024]))
# 输出层
W_output = tf.Variable(tf.truncated_normal([1024, 10]))
b_output = tf.Variable(tf.zeros([10]))
# feedforward
def inference(x):
# 首先要把
x_img = tf.reshape(x, [-1, 28, 28, 1])
# 卷积运算
convedActivations = tf.nn.relu(
tf.nn.conv2d(
x_img, W_conv, strides=[1, 1, 1, 1], padding='SAME') + b_conv)
# pooling
pooledActivations = tf.nn.max_pool(
convedActivations,
ksize=[1, 4, 4, 1],
strides=[1, 4, 4, 1],
padding='SAME')
# 隐藏层
pooledActivationsFlat = tf.reshape(pooledActivations, [-1, 7 * 7 * 64])
hiddenActivations = tf.nn.relu(tf.matmul(pooledActivationsFlat, W_hidden) + b_hidden)
# 输出层
logits = tf.matmul(hiddenActivations, W_output) + b_output
return logits
# 损失函数
def loss(x, y):
z = inference(x)
return tf.reduce_mean(
tf.nn.softmax_cross_entropy_with_logits(
labels=y, logits=z, name='xentropy'))
把这段代码放在框架里直接执行的话,会发现结果很差。原因是学习速率过大,导致损失函数不能收敛。只要把框架里learning_rate变量的值改为1e-3即可。
参考资料
- TensorFlow官方教程。学习开源项目,官方教程和文档永远是排在第一位的参考资料。尤其是Google这种大公司的开源项目,官方资料还是很靠谱的。
- 吴恩达(Andrew Ng)在Coursera上的机器学习在线课程,应该是最流行的机器学习教程了。内容深入浅出,非常适合入门。虽然刚开始不是很习惯吴恩达的口语发音,但是全套课程看下来,还是很喜欢这位老师的。课程中的实验使用的是Matlab/Octave,如果没有基础可能会感觉有点儿吃力,好在需要自己写的代码并不是很多,有时间还是建议都做一下,对理解算法很有帮助。我就是连蒙带猜加搜索,一点点啃下来的。
- Standford的Deep Learning Toturials。这个也是吴恩达那批人搞的,在2的基础上增加了深度学习的内容,内容上具有连贯性。学习过2之后,再通过这个教程进入深度学习,是很不错的选择。
- 《Tensorflow for Machine Intelligence》。既有TensorFlow的教程,也有关于机器学习和深度学习算法的讲解,对于初学者是很不错的入门参考。书中的实验代码都可以从Github上下载。需要注意的是,因为这本书出版得比较早,里面关于TensorFlow的部分内容已经过时,有些代码可能需要修改才能运行。
作者:FunFeast
链接:https://www.jianshu.com/p/f3c9ce8c0f20
來源:简书
简书著作权归作者所有,任何形式的转载都请联系作者获得授权并注明出处。