吴恩达机器学习第二次作业——逻辑回归
逻辑回归
- 一、逻辑回归
- 1,数据可视化
- 2,sigmoid函数,逻辑回归模型
- 3,代价函数以及梯度
- 4,评价逻辑回归
- 二、正规化逻辑回归
- 1,数据可视化
- 2,特征映射(Feature Mapping)
- 3,代价函数及梯度
一、逻辑回归
1,数据可视化
在这部分练习中,建立一个逻辑回归模型来预测一个学生是否被大学录取。
假设作为一所大学系的管理者,要根据每一位申请人在两次考试中的成绩来确定他们的入学机会。这里有前几年的历史数据 可以将其用作逻辑回归的培训集。对于每个培训示例,都有申请者在两次考试中的分数和招生决定。
定义plotData.m函数,可视化数据集,分布在二维平面
function plotData(X, y)
%PLOTDATA Plots the data points X and y into a new figure
% PLOTDATA(x,y) plots the data points with + for the positive examples
% and o for the negative examples. X is assumed to be a Mx2 matrix.
% Create New Figure
figure; hold on;
% ====================== YOUR CODE HERE ======================
% Instructions: Plot the positive and negative examples on a
% 2D plot, using the option 'k+' for the positive
% examples and 'ko' for the negative examples.
%
% Find Indices of Positive and Negative Examples
pos = find(y==1); neg = find(y == 0);
% Plot Examples
plot(X(pos, 1), X(pos, 2), 'k+','LineWidth', 2, ...
'MarkerSize', 7);
plot(X(neg, 1), X(neg, 2), 'ko', 'MarkerFaceColor', 'y', ...
'MarkerSize', 7);
% =========================================================================
hold off;
end
数据来自于大学入学数据,通过(Admitted)在图中用加号表示,不通过(Not Admitted)用圆表示。
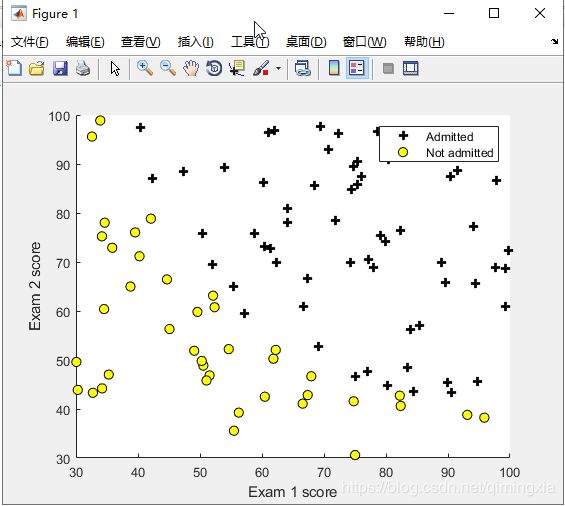
2,sigmoid函数,逻辑回归模型
在线性回归中,假设拟合直线函数为
h θ ( x ) = θ T x h_\theta(x)=\theta^{T}x hθ(x)=θTx
在逻辑回归中,我们希望
0 < = h θ ( x ) > = 1 0<=h_\theta(x)>=1 0<=hθ(x)>=1
此时,设逻辑回顾假设函数为:
h θ ( x ) = g ( θ T x ) h_\theta(x)=g(\theta^{T}x) hθ(x)=g(θTx)
其中,
g ( z ) = 1 1 + e − z g(z)=\frac{1}{1+e^{-z}} g(z)=1+e−z1
g ( z ) g(z) g(z)就是sigmoid函数,函数曲线如下
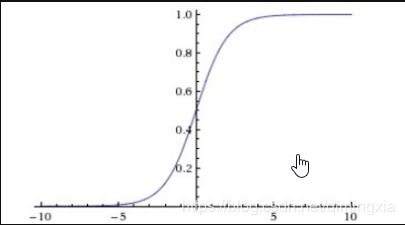
对于假设函数的解释: 假设函数的输出结果就是对于输入 x x x时,得到 y = 1 y=1 y=1的概率估计。
h θ ( x ) = p ( y = 1 ∣ x ; θ ) , y = 0 o r y = 1 h_\theta(x)=p(y=1|x;\theta), y=0ory=1 hθ(x)=p(y=1∣x;θ),y=0ory=1
显然有
p ( y = 1 ∣ x ; θ ) + p ( y = 0 ∣ x ; θ ) = 1 p(y=1|x;\theta)+p(y=0|x;\theta)=1 p(y=1∣x;θ)+p(y=0∣x;θ)=1
代码编写自定义函数sigmoid.m实现
function g = sigmoid(z)
%SIGMOID Compute sigmoid function
% g = SIGMOID(z) computes the sigmoid of z.
% You need to return the following variables correctly
g = zeros(size(z));
% ====================== YOUR CODE HERE ======================
% Instructions: Compute the sigmoid of each value of z (z can be a matrix,
% vector or scalar).
g = 1 ./ ( 1 + exp(-z) ) ;
% =============================================================
end
3,代价函数以及梯度
逻辑回归模型的代价函数为:
{ − l o g ( h θ ( x ) ) i f y = 1 − l o g ( 1 − h θ ( x ) ) i f y = 0 \left\{\begin{matrix} -log(h_\theta(x)) &if& y=1 \\-log(1-h_\theta(x)) & if &y=0 \end{matrix}\right. {−log(hθ(x))−log(1−hθ(x))ifify=1y=0
将上式合并
c o s t ( h θ ( x ) , y ) = − y log ( h θ ( x ) − ( 1 − y ) log ( 1 − h θ ( x ) ) ) cost(h_\theta(x),y)=-y\log(h_\theta(x)-(1-y)\log(1-h_\theta(x))) cost(hθ(x),y)=−ylog(hθ(x)−(1−y)log(1−hθ(x)))
J ( θ ) = 1 m ∑ i = 1 m c o s t ( h θ x ( i ) , y ( i ) ) J(\theta)=\frac{1}{m}\sum_{i=1}^{m}cost(h_\theta x^{(i)},y^{(i)}) J(θ)=m1∑i=1mcost(hθx(i),y(i))
J ( θ ) = − 1 m [ ∑ i = 1 m y ( i ) log ( h θ ( x ( i ) ) − ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] J(\theta)=-\frac{1}{m}[\sum_{i=1}^{m}y^{(i)}\log(h_\theta(x^{(i)})-(1-y^{(i)})\log(1-h_\theta(x^{(i)}))] J(θ)=−m1[∑i=1my(i)log(hθ(x(i))−(1−y(i))log(1−hθ(x(i)))]
在线性回归中使用梯度下降算法,这里也可以使用
循环下述赋值过程,直到 θ \theta θ收敛。
repeat{
θ j : = θ j − α ∂ ∂ / θ j J ( θ ) \theta_j:=\theta_j-\alpha\frac{\partial }{\partial /\theta_j}J(\theta) θj:=θj−α∂/θj∂J(θ)
}
这里的 ∂ ∂ / θ j J ( θ ) = − 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \frac{\partial }{\partial /\theta_j}J(\theta)=-\frac{1}{m}\sum_{i=1}^{m} (h_\theta(x^{(i)})-y^{(i)})x_j^{(i)} ∂/θj∂J(θ)=−m1∑i=1m(hθ(x(i))−y(i))xj(i)
但是,在此次实验中,使用高级优化函数fminunc,得到最后收敛的 θ \theta θ
代码实现:
function [J, grad] = costFunction(theta, X, y)
%COSTFUNCTION Compute cost and gradient for logistic regression
% J = COSTFUNCTION(theta, X, y) computes the cost of using theta as the
% parameter for logistic regression and the gradient of the cost
% w.r.t. to the parameters.
% Initialize some useful values
m = length(y); % number of training examples
% You need to return the following variables correctly
J = 0;
grad = zeros(size(theta));
% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost of a particular choice of theta.
% You should set J to the cost.
% Compute the partial derivatives and set grad to the partial
% derivatives of the cost w.r.t. each parameter in theta
%
% Note: grad should have the same dimensions as theta
%
J= -1 * sum( y .* log( sigmoid(X*theta) ) + (1 - y ) .* log( (1 - sigmoid(X*theta)) ) ) / m ;
grad = ( X' * (sigmoid(X*theta) - y ) )/ m ;
% =============================================================
end
根据由高级优化函数fminunc得到的 θ \theta θ,画出下图逻辑回归的分割边界
[theta, J, exit_flag] = fminunc(@(t)(costFunctionReg(t, X, y, lambda)), initial_theta, options);
简单说一下:
-
optimset(‘GradObj’, ‘on’, ‘MaxIter’, 400); 这句话中,<‘GradObj’, ‘on’>代表在fminunc函数中使用自定义的梯度下降函数 , < ‘MaxIter’, 400>代表最大迭代次数为400。
-
fminunc(@(t)(costFunction(t, X, y)), initial_theta, options); 这句话中,<@(t)(costFunction(t, X, y)>代表传入一个函数,@ 是一个句柄,类似于C中的指针。< initial_theta>是传入的theta矩阵。是一个optimset函数,对fminunc的属性进行一些设置。
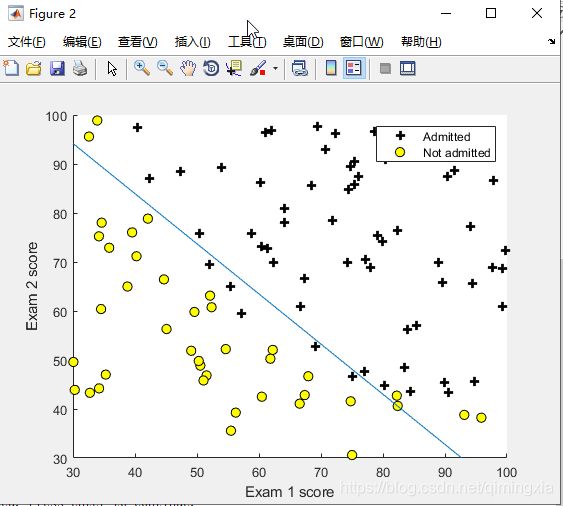
4,评价逻辑回归
在这次实验中,数据集是表征大学入学通过状况, h θ ( x ) > = 0.5 h_\theta(x)>=0.5 hθ(x)>=0.5时,预测结果为通过。
通过自定义函数predict.m代码实现:
function p = predict(theta, X)
%PREDICT Predict whether the label is 0 or 1 using learned logistic
%regression parameters theta
% p = PREDICT(theta, X) computes the predictions for X using a
% threshold at 0.5 (i.e., if sigmoid(theta'*x) >= 0.5, predict 1)
m = size(X, 1); % Number of training examples
% You need to return the following variables correctly
p = zeros(m, 1);
% ====================== YOUR CODE HERE ======================
% Instructions: Complete the following code to make predictions using
% your learned logistic regression parameters.
% You should set p to a vector of 0's and 1's
%
k = find(sigmoid( X * theta) >= 0.5 );
p(k)= 1; % k是输入数据中预测结果为1的数据的下标,令p向量中的这些分量为1。
% =========================================================================
end
由测试集得到该逻辑回归返回结果的准确率
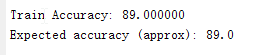
将预测结果与数据集真实结果比对,得到该逻辑回归判断结果的准确率为百分之八十九点零。可以看出,通过逻辑回归算法,能够较为有效得将两类特征区分开。
二、正规化逻辑回归
在练习的这一部分中,将实现正则逻辑回归,以预测来自制造厂的微芯片是否通过质量保证(QA)。在QA过程中,每个微芯片 进行各种测试以确保其正常运行。
假设作为工厂的产品经理,并且在两个不同的测试中获得了一些微芯片的测试结果。从这两个测试中,可以确定微芯片是否是 应接受或拒绝。为了帮助做出决策,有一个关于过去微芯片的测试结果的数据集,可以从中构建逻辑回归模型。
1,数据可视化
和上一部分数据可视化类似,也是使用plotDate.m函数,二维坐标的横坐标,纵坐标分别是两次测试的的得分,合格用加号表征(y = 1, accepted),不合格用圆表征(y = 0, rejected)。
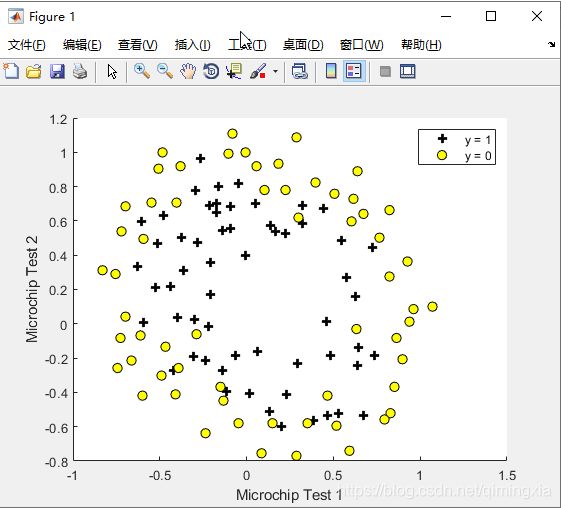
2,特征映射(Feature Mapping)
为了使数据得到更好的拟合,一个很好得方法是从数据点中创造更多得特征。创建mapFeature.m函数,将特征 x 1 , x 2 x_1,x_2 x1,x2映射到所有 x 1 , x 2 x_1,x_2 x1,x2的多项式,最高次幂设置为6次幂。

经过特征映射后,两个特征被映射为28维向量。在这个高维特征向量上训练的Logistic回归分类器将具有更复杂的决策边界,当在我们的二维图中绘制时会出现非线性。
mapFeature.m代码编译
function out = mapFeature(X1, X2)
% MAPFEATURE Feature mapping function to polynomial features
%
% MAPFEATURE(X1, X2) maps the two input features
% to quadratic features used in the regularization exercise.
%
% Returns a new feature array with more features, comprising of
% X1, X2, X1.^2, X2.^2, X1*X2, X1*X2.^2, etc..
%
% Inputs X1, X2 must be the same size
%
degree = 6;
out = ones(size(X1(:,1)));
for i = 1:degree
for j = 0:i
out(:, end+1) = (X1.^(i-j)).*(X2.^j);
end
end
end
虽然特征映射允许我们建立一个更有表现力的分类器,但它也更容易受到过度拟合的影响。在本练习的下一部分中,将实现正规化的逻辑回归。 继续对数据进行拟合,并学习正则化是如何帮助解决过度拟合问题的。
3,代价函数及梯度
正则化后的代价函数为:
J ( θ ) = − 1 m [ ∑ i = 1 m y ( i ) log ( h θ ( x ( i ) ) − ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] + λ 2 m ∑ j = 1 n θ j 2 J(\theta)=-\frac{1}{m}[\sum_{i=1}^{m}y^{(i)}\log(h_\theta(x^{(i)})-(1-y^{(i)})\log(1-h_\theta(x^{(i)}))]+\frac{\lambda}{2m}\sum_{j=1}^{n}\theta_j^2 J(θ)=−m1[∑i=1my(i)log(hθ(x(i))−(1−y(i))log(1−hθ(x(i)))]+2mλ∑j=1nθj2
∂ ∂ / θ 0 J ( θ ) = 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \frac{\partial }{\partial /\theta_0}J(\theta)=\frac{1}{m}\sum_{i=1}^{m} (h_\theta(x^{(i)})-y^{(i)})x_j^{(i)} ∂/θ0∂J(θ)=m1∑i=1m(hθ(x(i))−y(i))xj(i) f o r j = 0 for j=0 forj=0
∂ ∂ / θ j J ( θ ) = ( 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) ) + λ m θ j \frac{\partial }{\partial /\theta_j}J(\theta)=(\frac{1}{m}\sum_{i=1}^{m} (h_\theta(x^{(i)})-y^{(i)})x_j^{(i)})+\frac{\lambda}{m}\theta_j ∂/θj∂J(θ)=(m1∑i=1m(hθ(x(i))−y(i))xj(i))+mλθj f o r j > = 1 for j>=1 forj>=1
function [J, grad] = costFunctionReg(theta, X, y, lambda)
%COSTFUNCTIONREG Compute cost and gradient for logistic regression with regularization
% J = COSTFUNCTIONREG(theta, X, y, lambda) computes the cost of using
% theta as the parameter for regularized logistic regression and the
% gradient of the cost w.r.t. to the parameters.
% Initialize some useful values
m = length(y); % number of training examples
% You need to return the following variables correctly
J = 0;
grad = zeros(size(theta));
% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost of a particular choice of theta.
% You should set J to the cost.
% Compute the partial derivatives and set grad to the partial
% derivatives of the cost w.r.t. each parameter in theta
h=sigmoid(X*theta);
theta(1,1)=0;
J=sum(-y'*log(h)-(1-y)'*log(1-h))/m+lambda/2/m*sum(power(theta,2));
grad=((h-y)'*X)/m+lambda/m*theta';
% =============================================================
end
通过计算得到代价函数,以及梯度,运用ex1中的高级优化函数fminunc来得到满足最佳拟合的 θ \theta θ值
附上正则化逻辑回归完整代码
%% Machine Learning Online Class - Exercise 2: Logistic Regression
%
% Instructions
% ------------
%
% This file contains code that helps you get started on the second part
% of the exercise which covers regularization with logistic regression.
%
% You will need to complete the following functions in this exericse:
%
% sigmoid.m
% costFunction.m
% predict.m
% costFunctionReg.m
%
% For this exercise, you will not need to change any code in this file,
% or any other files other than those mentioned above.
%
%% Initialization
clear ; close all; clc
%% Load Data
% The first two columns contains the X values and the third column
% contains the label (y).
data = load('ex2data2.txt');
X = data(:, [1, 2]); y = data(:, 3);
plotData(X, y);
% Put some labels
hold on;
% Labels and Legend
xlabel('Microchip Test 1')
ylabel('Microchip Test 2')
% Specified in plot order
legend('y = 1', 'y = 0')
hold off;
%% =========== Part 1: Regularized Logistic Regression ============
% In this part, you are given a dataset with data points that are not
% linearly separable. However, you would still like to use logistic
% regression to classify the data points.
%
% To do so, you introduce more features to use -- in particular, you add
% polynomial features to our data matrix (similar to polynomial
% regression).
%
% Add Polynomial Features
% Note that mapFeature also adds a column of ones for us, so the intercept
% term is handled
X = mapFeature(X(:,1), X(:,2));
% Initialize fitting parameters
initial_theta = zeros(size(X, 2), 1);
% Set regularization parameter lambda to 1
lambda = 1;
% Compute and display initial cost and gradient for regularized logistic
% regression
[cost, grad] = costFunctionReg(initial_theta, X, y, lambda);
fprintf('Cost at initial theta (zeros): %f\n', cost);
fprintf('Expected cost (approx): 0.693\n');
fprintf('Gradient at initial theta (zeros) - first five values only:\n');
fprintf(' %f \n', grad(1:5));
fprintf('Expected gradients (approx) - first five values only:\n');
fprintf(' 0.0085\n 0.0188\n 0.0001\n 0.0503\n 0.0115\n');
fprintf('\nProgram paused. Press enter to continue.\n');
pause;
% Compute and display cost and gradient
% with all-ones theta and lambda = 10
test_theta = ones(size(X,2),1);
[cost, grad] = costFunctionReg(test_theta, X, y, 10);
fprintf('\nCost at test theta (with lambda = 10): %f\n', cost);
fprintf('Expected cost (approx): 3.16\n');
fprintf('Gradient at test theta - first five values only:\n');
fprintf(' %f \n', grad(1:5));
fprintf('Expected gradients (approx) - first five values only:\n');
fprintf(' 0.3460\n 0.1614\n 0.1948\n 0.2269\n 0.0922\n');
fprintf('\nProgram paused. Press enter to continue.\n');
pause;
%% ============= Part 2: Regularization and Accuracies =============
% Optional Exercise:
% In this part, you will get to try different values of lambda and
% see how regularization affects the decision coundart
%
% Try the following values of lambda (0, 1, 10, 100).
%
% How does the decision boundary change when you vary lambda? How does
% the training set accuracy vary?
%
% Initialize fitting parameters
initial_theta = zeros(size(X, 2), 1);
% Set regularization parameter lambda to 1 (you should vary this)
lambda = 1;
% Set Options
options = optimset('GradObj', 'on', 'MaxIter', 400);
% Optimize
[theta, J, exit_flag] = ...
fminunc(@(t)(costFunctionReg(t, X, y, lambda)), initial_theta, options);
% Plot Boundary
plotDecisionBoundary(theta, X, y);
hold on;
title(sprintf('lambda = %g', lambda))
% Labels and Legend
xlabel('Microchip Test 1')
ylabel('Microchip Test 2')
legend('y = 1', 'y = 0', 'Decision boundary')
hold off;
% Compute accuracy on our training set
p = predict(theta, X);
fprintf('Train Accuracy: %f\n', mean(double(p == y)) * 100);
fprintf('Expected accuracy (with lambda = 1): 83.1 (approx)\n');
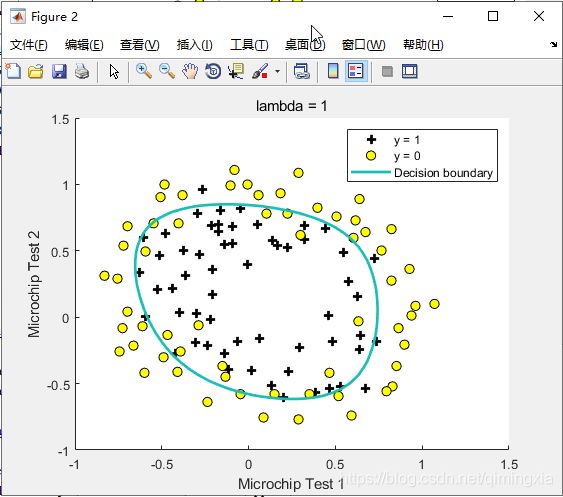
通过特征映射,使两个特征映射到28维向量,得到了非线性的分割边界。由于特征向量过多,为了防止由此产生的过拟合现象,采用正则化算法,利用正则化参数 λ \lambda λ对 θ \theta θ进行惩罚,完成较好的拟合分离边界效果。如上图结果显示,分离边界已经很好地完成了任务。
![]()
运行代码后,结果显示预测结果正确率为0.831