吴恩达机器学习第二道编程题logistic逻辑回归

主程序logistic.m：

A=load('tumor_size.txt');%肿瘤尺寸
B=load('tumor_type.txt');%肿瘤性质，0良性1恶性
C=[ones(length(B),1),A];
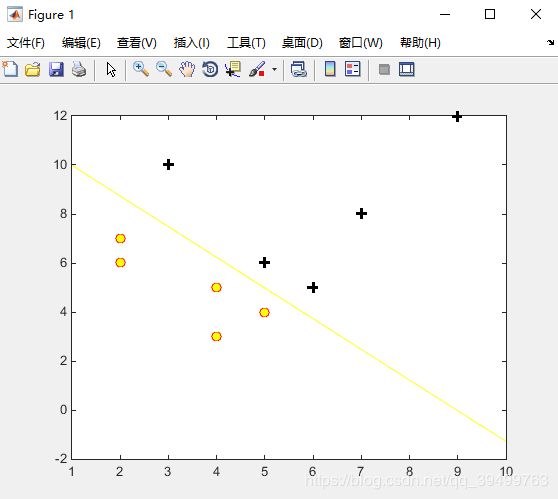
%画出数据集
pos=find(B==1);neg=find(B==0);
plot(A(pos,1),A(pos,2),'k+','Linewidth',2,'MarkerSize',7);hold on;
plot(A(neg,1),A(neg,2),'ro','MarkerFaceColor','y','MarkerSize',7);
m=length(B);%样本个数
theta=ones(3,1);%假设函数参数初始化
alfa=0.01 ;%设置学习率
Jvec=zeros(1000,1);%用来存放收敛过程中的代价函数值，用于判断学习率是否合适 
h_theta=cal_h(theta,C,m);
Jvec(1,1)=log_cal_j(h_theta,B);%计算第一个代价函数值
theta(1,1)=theta(1,1)-alfa/m*sum((h_theta-B).*C(:,1));%更新theta
theta(2,1)=theta(2,1)-alfa/m*sum((h_theta-B).*C(:,2));
theta(3,1)=theta(3,1)-alfa/m*sum((h_theta-B).*C(:,3));
h_theta=cal_h(theta,C,m);
Jvec(2,1)=log_cal_j(h_theta,B);%计算第二个代价函数值
ii=2;
while Jvec(ii-1,1)-Jvec(ii,1)>=0.0000001%设置参数更新的终止条件：如果先后两个代价
    ii=ii+1;                            %函数值的减小幅度小于0.0000001，则终止
    theta(1,1)=theta(1,1)-alfa/m*sum((h_theta-B).*C(:,1));
    theta(2,1)=theta(2,1)-alfa/m*sum((h_theta-B).*C(:,2));
    theta(3,1)=theta(3,1)-alfa/m*sum((h_theta-B).*C(:,3));
    h_theta=cal_h(theta,C,m);
    Jvec(ii,1)=log_cal_j(h_theta,B);
end
hold on;
x=[1:10];
y=(ones(length(x),1)*theta(1,1)+theta(2,1)*x')/(-theta(3,1));
plot(x,y','y');%画出决策边界
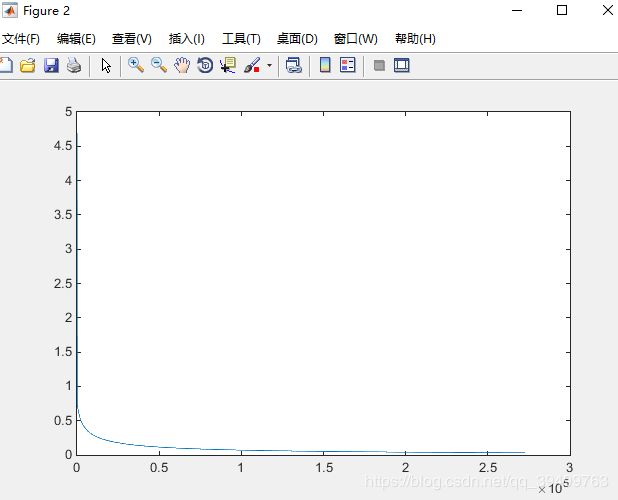
figure;
plot(Jvec);%axis([0 10 0 60000]);

计算假设函数值cal_h.m

function h=cal_h(theta,X,m)%计算假设函数值
h=zeros(m,1);
for i=1:m
z=theta'*X(i,:)';
h(i,1)=1/(1+exp(-z));
end
end

计算代价函数log_cal_j.m

function j=log_cal_j(h_theta,y)%计算代价函数值
m=length(y);
h1=log(h_theta);h2=log(ones(m,1)-h_theta);
j=sum(y.*h1+(ones(m,1)-y).*h2)/(-m);
end

数据集tumor_size.txt

4 3
2 6
7 8
5 4
9 12
6 5
3 10
2 7
4 5
5 6

还有tumor_type.txt

0
0
1
0
1
1
1
0
0
1

运行结果：
数据集和决策边界：

代价函数：

欢迎学习吴恩达机器学习的朋友一起交流进步！