备战秋招-LeetCode 打卡-二叉树的前序遍历、中序遍历、后序遍历（递归、数、栈）

给定一个二叉树，返回它的前序遍历、中序遍历、后序遍历

示例:

输入: [1,null,2,3]
   1
    \
     2
    /
   3

输出: [1,3,2]

进阶: 递归算法很简单，你可以通过迭代算法完成吗？

leetcode上的一道题目，前序中序后序都有，我直接整合到一起了，对树的遍历有了一个总结。代码同时用递归和栈的两种方法，其实你认真思考一下递归的整个过程不就是先进后出吗，刚刚好可以用栈来代替递归。

以前序遍历为例：

前序遍历首先访问根结点然后遍历左子树，最后遍历右子树。在遍历左、右子树时，仍然先访问根结点，然后遍历左子树，最后遍历右子树。
若二叉树为空则结束返回，否则：

（1）访问根结点。
（2）前序遍历左子树。
（3）前序遍历右子树。

需要注意的是：遍历左右子树时仍然采用前序遍历方法。

以下面这棵树的先序遍历为例，把这例子搞懂了，三种遍历都是一样的。文字有点多有点枯燥，拿着笔对着文字和图画一下就明白了。

              1
           /     \
          2       3
        /   \   /   \
       4    5  6     7

当前根节点为1，先存储根节点1，然后再遍历以2为根节点的左子树，最后再遍历以3为根节点的右子树。 已遍历的节点顺序为1

当前根节点为2，先存储根节点2，然后再遍历以4为根节点的左子树，最后再遍历以5为根节点的右子树。 已遍历的节点顺序为1>>2

当前根节点为4，先存储根节点4，以4为根节点的左右子树均为空，所以不用再往下遍历了， 已遍历的节点顺序为1>>2>>4

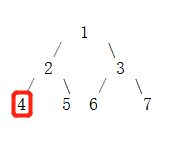
此时以2为根节点的左子树已经遍历完了，我们继续遍历以2位根节点的右子树。根节点为5，存储下来，以5位根节点的左右子树均为空，所以不用再往下遍历了，已遍历的节点顺序为1>>2>>4>>5。

以1为根节点的左子树以全部遍历完，继续遍历以3为根节点的左子树，然后遍历以3为根节点的右子树。当前根节点为3，存储下来，已遍历的节点顺序为1>>2>>4>>5>>3。

当前根节点为6，存储下来。以6为根节点的左右子树均为空，所以不用再往下遍历了， 已遍历的节点顺序为1>>2>>4>>5>>3>>6。

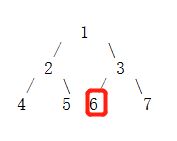
此时以3为根节点的左子树已遍历完，继续遍历以3为根节点的右子树。当前根节点为6，存储下来。以6为根节点的左右子树均为空，所以不用再问下遍历了， 已遍历的节点顺1>>2>>4>>5>>3>>6>>7,全部遍历完成。

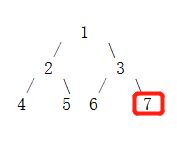
中序遍历、后续遍历都是一样的，就不一一细说了，接下来贴代码，建议先看递归版本的代码，比较容易懂。

前序遍历递归版本参考代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List preorderTraversal(TreeNode root) {
        List al=new ArrayList();
		inorder(al, root);
		System.out.println(al);
		return al;
    }
    public void inorder(List al,TreeNode root)
	{
		if(root==null)
			return ;
		al.add(root.val);
		inorder(al, root.left);
		inorder(al, root.right);
	}
}

前序遍历的迭代版本参考代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List preorderTraversal(TreeNode root) {
        List al=new ArrayList();
		Stack st=new Stack();
		TreeNode p=root;
		while(p!=null||!st.isEmpty())
		{
			while(p!=null)
			{
				al.add(p.val);
				st.push(p);
				p=p.left;
			}
			TreeNode temp = st.pop();
			//al.add(temp.val);
			p=temp.right;
		}
		System.out.println(al);
		return al;
    }
}

中序遍历递归版本参考代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List inorderTraversal(TreeNode root) 
	{
		List al=new ArrayList();
		inorder(al, root);
		System.out.println(al);
		return al;
    }
	public void inorder(List al,TreeNode root)
	{
		if(root==null)
			return ;
		inorder(al, root.left);
		al.add(root.val);
		inorder(al, root.right);
	}
}

中序遍历迭代版本参考代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List inorderTraversal(TreeNode root) 
	{
		List al=new ArrayList();
		Stack st=new Stack();
		TreeNode p=root;
		while(p!=null||!st.isEmpty())
		{
			while(p!=null)
			{
				st.push(p);
				p=p.left;
			}
			TreeNode temp = st.pop();
			al.add(temp.val);
			p=temp.right;
		}
		System.out.println(al);
		return al;
    }
}

后序遍历递归版本参考代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List postorderTraversal(TreeNode root) {
        List al=new ArrayList();
		inorder(al, root);
		System.out.println(al);
		return al;
    }
    public void inorder(List al,TreeNode root)
	{
		if(root==null)
			return ;
		inorder(al, root.left);
		inorder(al, root.right);
		al.add(root.val);		
	}
}

后序遍历迭代版本参考代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
     public List postorderTraversal(TreeNode root) {
    LinkedList stack = new LinkedList<>();
    LinkedList output = new LinkedList<>();
    if (root == null) {
      return output;
    }

    stack.add(root);
    while (!stack.isEmpty()) {
      TreeNode node = stack.pollLast();
      output.addFirst(node.val);
      if (node.left != null) {
        stack.add(node.left);
      }
      if (node.right != null) {
        stack.add(node.right);
      }
    }
    return output;
  }

}