LDA原理(剖析源代码,详解)
上篇文章我们讲解了PCA的原理,在这里我们先分析一下PCA和LDA的区别
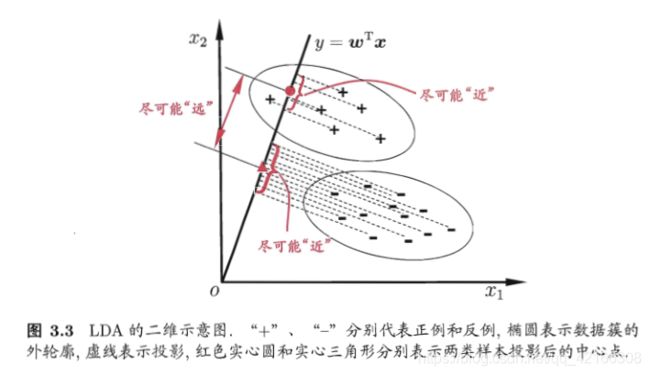
LDA线性判别分析也是一种经典的降维方法,LDA是一种监督学习的降维技术,也就是说它的数据集的每个样本是有类别输出的。这点和PCA不同。PCA是不考虑样本类别输出的无监督降维技术。LDA的思想可以用一句话概括,就是“投影后类内方差最小,类间方差最大”。
什么意思呢? 我们要将数据在低维度上进行投影,投影后希望每一种类别数据的投影点尽可能的接近,而不同类别的数据的类别中心之间的距离尽可能的大。
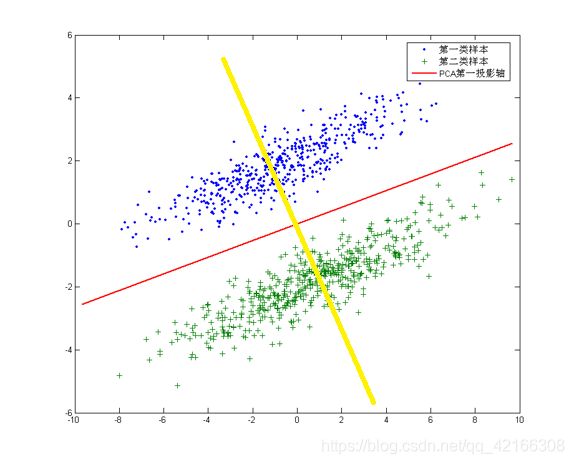
可能还是有点抽象,我们先看看最简单的情况。假设我们有两类数据分别为红色和蓝色,如下图所示,这些数据特征是二维的,我们希望将这些数据投影到一维的一条直线,让每一种类别数据的投影点尽可能的接近,而红色和蓝色数据中心之间的距离尽可能的大。
左边是PCA的投影效果,右边是LDA的投影效果。可以看出PCA只是考虑了整体的情况,投影到方差最大的方向,而LDA投影的时候考虑到类内方差减小,类间方差增大,这样可以更好的进行区分。
针对这个数据集,如果同样选择使用PCA,选择方差最大的方向作为投影方向,来对数据进行降维。那么PCA选出的最佳投影方向,将是图中红色直线所示的方向。这样做投影确实方差最大,但是是不是有其他问题。聪明的你一定发现了,这样做投影之后两类数据样本将混合在一起,将不再线性可分,甚至是不可分的。这对我们来说简直就是地狱,本来线性可分的样本被我们亲手变得不再可分。
帅气英俊的你也一定发现了,图中还有一条耀眼的黄色直线,向这条直线做投影即能使数据降维,同时还能保证两类数据仍然是线性可分的。上面的这个数据集如果使用LDA降维,找出的投影方向就是黄色直线所在的方向。
这其实就是LDA的思想,或者说LDA降维的目标:将带有标签的数据降维,投影到低维空间同时满足三个条件:
尽可能多地保留数据样本的信息(即选择最大的特征是对应的特征向量所代表的的方向)。
寻找使样本尽可能好分的最佳投影方向。
投影后使得同类样本尽可能近,不同类样本尽可能远。
两者的相同点是:
1)两者均可以对数据进行降维。
2)两者在降维时均使用了矩阵特征分解的思想。
3)两者都假设数据符合高斯分布【正态分布】。
两者的不同点是:
1)LDA是有监督的降维方法,而PCA是无监督的降维方法
2)LDA降维最多降到类别数**k-1**的维数,而PCA没有这个限制。
3)LDA除了可以用于降维,还可以用于分类。(有predict方法,而PCA没有)
4)LDA选择分类性能最好的投影方向,而PCA选择样本点投影具有最大方差的方向。
下面开始进行分析它是如何计算出来的?
在这里我们还是使用鸢尾花的数据进行分析(属性较少,更直观,容易理解!)
import numpy as np
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn import datasets
import warnings
warnings.filterwarnings('ignore')
X,y = datasets.load_iris(True)
X[:5]
array([[5.1, 3.5, 1.4, 0.2],
[4.9, 3. , 1.4, 0.2],
[4.7, 3.2, 1.3, 0.2],
[4.6, 3.1, 1.5, 0.2],
[5. , 3.6, 1.4, 0.2]])
为了验证我们计算的准确无误,下面是对原码进行剖析的结果,我在源代码中进行了修改,打印了Sw,St,Sb的准确值,用来比较
如下图是源代码,在这里我们主要是对solver='eigen’这种情况进行剖析(比较常用)
class LinearDiscriminantAnalysis(BaseEstimator, LinearClassifierMixin,
TransformerMixin):
def _solve_eigen(self, X, y, shrinkage):
Sw = self.covariance_ # within scatter
print('------Sw为',Sw)
St = _cov(X, shrinkage) # total scatter
print('******St为',St)
Sb = St - Sw # between scatter
print('++++++Sb为',Sb)
evals, evecs = linalg.eigh(Sb, Sw)
print('------evals',evals)
self.explained_variance_ratio_ = np.sort(evals / np.sum(evals)
)[::-1][:self._max_components]
evecs = evecs[:, np.argsort(evals)[::-1]] # sort eigenvectors
# 特征值和特征向量
lda = LinearDiscriminantAnalysis(solver='eigen',n_components=2)
X_lda = lda.fit_transform(X,y)
X_lda[:5]
------Sw为 [[0.259708 0.09086667 0.164164 0.03763333]
[0.09086667 0.11308 0.05413867 0.032056 ]
[0.164164 0.05413867 0.181484 0.041812 ]
[0.03763333 0.032056 0.041812 0.041044 ]]
******St为 [[ 0.68112222 -0.04215111 1.26582 0.51282889]
[-0.04215111 0.18871289 -0.32745867 -0.12082844]
[ 1.26582 -0.32745867 3.09550267 1.286972 ]
[ 0.51282889 -0.12082844 1.286972 0.57713289]]
++++++Sb为 [[ 0.42141422 -0.13301778 1.101656 0.47519556]
[-0.13301778 0.07563289 -0.38159733 -0.15288444]
[ 1.101656 -0.38159733 2.91401867 1.24516 ]
[ 0.47519556 -0.15288444 1.24516 0.53608889]]
------evals [-2.16757273e-14 6.63220529e-15 2.85391043e-01 3.21919292e+01]
array([[6.01716893, 7.03257409],
[5.0745834 , 5.9344564 ],
[5.43939015, 6.46102462],
[4.75589325, 6.05166375],
[6.08839432, 7.24878907]])
1、总的散度矩阵
# 协方差
St = np.cov(X.T,bias = 1)
St
array([[ 0.68112222, -0.04215111, 1.26582 , 0.51282889],
[-0.04215111, 0.18871289, -0.32745867, -0.12082844],
[ 1.26582 , -0.32745867, 3.09550267, 1.286972 ],
[ 0.51282889, -0.12082844, 1.286972 , 0.57713289]])
!!注意这里为什么使用bias=1?(重点)答案也是剖析源代码得出结果:
def _cov(X, shrinkage=None):
shrinkage = "empirical" if shrinkage is None else shrinkage
if isinstance(shrinkage, str):
if shrinkage == 'auto':
sc = StandardScaler() # standardize features
X = sc.fit_transform(X)
s = ledoit_wolf(X)[0]
# rescale
s = sc.scale_[:, np.newaxis] * s * sc.scale_[np.newaxis, :]
elif shrinkage == 'empirical':
s = empirical_covariance(X)
else:
raise ValueError('unknown shrinkage parameter')
从上面部分代码可以看出,我们对shrinkage没有设置所以会执行s = empirical_covariance(X)步,好奇的我就会点进去,一探究竟,果然!!
if assume_centered:
covariance = np.dot(X.T, X) / X.shape[0]
else:
covariance = np.cov(X.T, bias=1)
if covariance.ndim == 0:
covariance = np.array([[covariance]])
return covariance
bias=1乖乖浮出浮出水面,这会就会发现不会有小的误差,准确至极~~
2、类内的散度矩阵
# Scatter散点图,within(内)
Sw = np.full(shape = (4,4),fill_value=0,dtype=np.float64)
for i in range(3):
Sw += np.cov(X[y == i],rowvar = False,bias = 1)
Sw/=3
Sw
array([[0.259708 , 0.09086667, 0.164164 , 0.03763333],
[0.09086667, 0.11308 , 0.05413867, 0.032056 ],
[0.164164 , 0.05413867, 0.181484 , 0.041812 ],
[0.03763333, 0.032056 , 0.041812 , 0.041044 ]])
3、计算类间的散度矩阵
# Scatter between
Sb = St - Sw
Sb
array([[ 0.42141422, -0.13301778, 1.101656 , 0.47519556],
[-0.13301778, 0.07563289, -0.38159733, -0.15288444],
[ 1.101656 , -0.38159733, 2.91401867, 1.24516 ],
[ 0.47519556, -0.15288444, 1.24516 , 0.53608889]])
# scipy这个模块下的线性代数子模块
from scipy import linalg
4、特征值,和特征向量
eigen,ev = linalg.eigh(Sb,Sw)
display(eigen,ev)
ev = ev[:, np.argsort(eigen)[::-1]]
ev
array([-1.84103303e-14, 1.18322589e-14, 2.85391043e-01, 3.21919292e+01])
array([[ 1.54162331, -2.82590065, 0.02434685, 0.83779794],
[-2.49358543, 1.05970269, 2.18649663, 1.55005187],
[-2.86907801, 1.01439507, -0.94138258, -2.22355955],
[ 4.58628831, 0.45101349, 2.86801283, -2.83899363]])
array([[ 0.83779794, 0.02434685, -2.82590065, 1.54162331],
[ 1.55005187, 2.18649663, 1.05970269, -2.49358543],
[-2.22355955, -0.94138258, 1.01439507, -2.86907801],
[-2.83899363, 2.86801283, 0.45101349, 4.58628831]])
这里的ev[:, np.argsort(eigen)[::-1]]为什么要进行这样的转换?
看源码!就可以知道答案啦~~
class LinearDiscriminantAnalysis(BaseEstimator, LinearClassifierMixin,
TransformerMixin):
def _solve_eigen(self, X, y, shrinkage):
Sw = self.covariance_ # within scatter
print('------Sw为',Sw)
St = _cov(X, shrinkage) # total scatter
print('******St为',St)
Sb = St - Sw # between scatter
print('++++++Sb为',Sb)
evals, evecs = linalg.eigh(Sb, Sw)
print('------evals',evals)
self.explained_variance_ratio_ = np.sort(evals / np.sum(evals)
)[::-1][:self._max_components]
evecs = evecs[:, np.argsort(evals)[::-1]] # sort eigenvectors
X_lda[:5]
array([[6.01716893, 7.03257409],
[5.0745834 , 5.9344564 ],
[5.43939015, 6.46102462],
[4.75589325, 6.05166375],
[6.08839432, 7.24878907]])
5、删选特征向量,进行矩阵运算
X.dot(ev)[:,:2]
array([[ 6.01716893, 7.03257409],
[ 5.0745834 , 5.9344564 ],
[ 5.43939015, 6.46102462],
[ 4.75589325, 6.05166375],
[ 6.08839432, 7.24878907],
[ 5.65366246, 8.20566459],
.........
可以看出,原码交给我们的真的是受益匪浅,答案准确无误!完美!