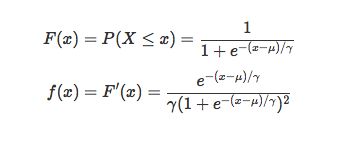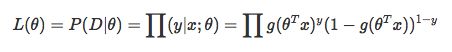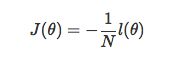西瓜书-逻辑回归算法的使用

1.任务名称：实验-sklearn-user-guide 1.1.11

2.使用包：sklearn（里面提供了许多机器学习算法的详细教程和案例，需要多多掌握）

3.资料地址：http://sklearn.apachecn.org/#/docs/79

逻辑回归

逻辑回归（Logistic regression 或logit regression），即逻辑模型（英语：Logit model，也译作“评定模型”、“分类评定模型”）是离散选择法模型之一，属于多重变量分析范畴，是社会学、生物统计学、临床、数量心理学、计量经济学、市场营销等统计实证分析的常用方法。——维基百科

虽然叫做回归其实是个分类模型。逻辑回归实际上是用sigmoid函数将线性回归进行了归一化，把输出值压缩到0-1之间，这个值代表的是发生的概率。

逻辑函数

逻辑函数（sigmoid函数）定义的累计分布又叫逻辑斯蒂分布，对分布函数求导得到概率密度函数。公式如下。[1]

[2]

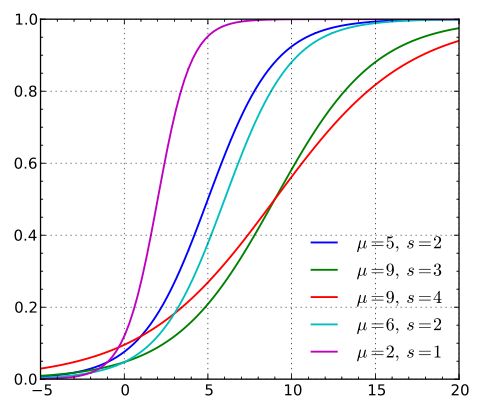
不同参数对逻辑分布的影响

 

图1 不同参数对逻辑分布的影响

注：图中s就是统计中的γ。

逻辑回归

逻辑回归是为了解决分类问题（主要是二分类），根据一些已知的训练集训练好模型，再对新的数据进行预测属于哪个类。比如用户是否点击某个广告、肿瘤是否是恶性的、用户的性别，等等。

逻辑回归需要找到分类概率P(Y=1)与输入向量x的直接关系，然后通过比较概率值来判断类别，这就用到上文中逻辑函数。它令决策函数的输出值$w^Tx+b$等于概率值比值取对数$log\frac{P(Y=1|x)}{1-P(Y=1|x)}$，求解这个式子得到了输入向量x下导致产生两类的概率为:

其中w称为权重，b称为偏置，其中的w⋅x+b看成对x的线性函数。然后对比上面两个概率值，概率值大的就是x对应的类。

对逻辑回归的定义，输出Y=1的对数几率是由输入x的线性函数表示的模型，即逻辑斯蒂回归模型(李航.《统计机器学习》)。

直接考察公式1可以得到另一种对逻辑回归的定义，线性函数的值越接近正无穷，概率值就越接近1；线性值越接近负无穷，概率值越接近0，这样的模型是逻辑斯蒂回归模型(李航.《统计机器学习》)。

因此逻辑回归的思路是，先拟合决策边界(这里的决策边界不局限于线性，还可以是多项式)，再建立这个边界与分类的概率联系，从而得到了二分类情况下的概率。这里有个非常棒的博文[6]推荐，阐述了逻辑回归的思路。

Logistic回归模型的适用条件

1. 因变量为二分类的分类变量或某事件的发生率，并且是数值型变量。但是需要注意，重复计数现象指标不适用于Logistic回归。

2. 残差和因变量都要服从二项分布。二项分布对应的是分类变量，所以不是正态分布，进而不是用最小二乘法，而是最大似然法来解决方程估计和检验问题。

3. 自变量和Logistic概率是线性关系

4. 各观测对象间相互独立。

原理：如果直接将线性回归的模型扣到Logistic回归中，会造成方程二边取值区间不同和普遍的非直线关系。因为Logistic中因变量为二分类变量，某个概

率作为方程的因变量估计值取值范围为0-1，但是，方程右边取值范围是无穷大或者无穷小。所以，才引入Logistic回归。

Logistic回归实质：发生概率除以没有发生概率再取对数。就是这个不太繁琐的变换改变了取值区间的矛盾和因变量自变量间的曲线关系。究其原因，是发生和未发生的概率成为了比值，这个比值就是一个缓冲，将取值范围扩大，再进行对数变换，整个因变量改变。不仅如此，这种变换往往使得因变量和自变量之间呈线性关系，这是根据大量实践而总结。所以，Logistic回归从根本上解决因变量要不是连续变量怎么办的问题。还有，Logistic应用广泛的原因是许多现实问题跟它的模型吻合。例如一件事情是否发生跟其他数值型自变量的关系。[3]

求解/优化

数学模型的形式确定之后，接下来就要求解参数。统计学中常用的一种方法是最大似然估计，即找到一组参数，使得在这组参数下，我们的数据的似然度（概率）越大。

在逻辑回归中，似然度为：

取对数得到对数似然度：

逻辑回归中最大化似然函数和最小化log损失函数实际上是等价的。

损失函数（loss function）是用来估量你模型的预测值f(x)与真实值Y的不一致程度，它是一个非负实值函数,通常使用L(Y, f(x))来表示，损失函数越小，模型的鲁棒性就越好[4]。常用的损失函数有0-1损失，log损失，hinge损失等。

优化的主要目标是找到一个方向，参数朝这个方向移动之后使得似然函数的值能够减小，这个方向往往由一阶偏导或者二阶偏导各种组合求得。逻辑回归的优化方法有很多，比如梯度下降，牛顿法和BFGS。

正则化

过拟合：提高在训练数据上的表现时，在测试数据上反而下降，这就被称为过拟合。

image

图2 同样数据下欠拟合，拟合和过拟合

所以要用正则化来限制模型参数，也叫惩罚项。正则化不是只有逻辑回归存在，它是一个通用的算法和思想，所以会产生过拟合现象的算法都可以使用正则化来避免过拟合。一般是在目标函数(经验风险)中加上一个正则化项Φ(w)。

啊~~~数学太差，看到公式就脑仁疼。

接下来去python里试试吧。

SKlearn实现逻辑回归

方法与参数

LogisticRegression类的各项参数的含义

class sklearn.linear_model.LogisticRegression(penalty='l2', 
          dual=False, tol=0.0001, C=1.0, fit_intercept=True, 
          intercept_scaling=1, class_weight=None, 
          random_state=None, solver='liblinear', max_iter=100, 
          multi_class='ovr', verbose=0, warm_start=False, n_jobs=1)

• penalty='l2' : 字符串‘l1’或‘l2’,默认‘l2’。
  • 用来指定惩罚的基准（正则化参数）。只有‘l2’支持‘newton-cg’、‘sag’和‘lbfgs’这三种算法。
  • 如果选择‘l2’，solver参数可以选择‘liblinear’、‘newton-cg’、‘sag’和‘lbfgs’这四种算法；如果选择‘l1’的话就只能用‘liblinear’算法。
• dual=False : 对偶或者原始方法。Dual只适用于正则化相为l2的‘liblinear’的情况，通常样本数大于特征数的情况下，默认为False。
• C=1.0 : C为正则化系数λ的倒数，必须为正数，默认为1。和SVM中的C一样，值越小，代表正则化越强。
• fit_intercept=True : 是否存在截距，默认存在。
• intercept_scaling=1 : 仅在正则化项为‘liblinear’，且fit_intercept设置为True时有用。
• solver='liblinear' : solver参数决定了我们对逻辑回归损失函数的优化方法，有四种算法可以选择。
  • a) liblinear：使用了开源的liblinear库实现，内部使用了坐标轴下降法来迭代优化损失函数。
  • b) lbfgs：拟牛顿法的一种，利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
  • c) newton-cg：也是牛顿法家族的一种，利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
  • d) sag：即随机平均梯度下降，是梯度下降法的变种，和普通梯度下降法的区别是每次迭代仅仅用一部分的样本来计算梯度，适合于样本数据多的时候。

从上面的描述可以看出，newton-cg、lbfgs和sag这三种优化算法时都需要损失函数的一阶或者二阶连续导数，因此不能用于没有连续导数的L1正则化，只能用于L2正则化。而liblinear通吃L1正则化和L2正则化。
同时，sag每次仅仅使用了部分样本进行梯度迭代，所以当样本量少的时候不要选择它，而如果样本量非常大，比如大于10万，sag是第一选择。但是sag不能用于L1正则化，所以当你有大量的样本，又需要L1正则化的话就要自己做取舍了。要么通过对样本采样来降低样本量，要么回到L2正则化。
但是liblinear也有自己的弱点！我们知道，逻辑回归有二元逻辑回归和多元逻辑回归。对于多元逻辑回归常见的有one-vs-rest(OvR)和many-vs-many(MvM)两种。而MvM一般比OvR分类相对准确一些。而liblinear只支持OvR，不支持MvM，这样如果我们需要相对精确的多元逻辑回归时，就不能选择liblinear了。也意味着如果我们需要相对精确的多元逻辑回归不能使用L1正则化了。

总结：

正则化	算法	适用场景
L1	liblinear	liblinear适用于小数据集；如果选择L2正则化发现还是过拟合，即预测效果差的时候，就可以考虑L1正则化；如果模型的特征非常多，希望一些不重要的特征系数归零，从而让模型系数稀疏化的话，也可以使用L1正则化。
L2	liblinear	libniear只支持多元逻辑回归的OvR，不支持MvM，但MVM相对精确。
L2	lbfgs/newton-cg/sag	较大数据集，支持one-vs-rest(OvR)和many-vs-many(MvM)两种多元逻辑回归。
L2	sag	如果样本量非常大，比如大于10万，sag是第一选择；但不能用于L1正则化。

来源：http://jishu.y5y.com.cn/cherdw/article/details/54891073

• multi_class='ovr' : 分类方式。官网有个对比两种分类方式的例子：链接地址。
  • ovr即one-vs-rest(OvR)，multinomial是many-vs-many(MvM)。如果是二元逻辑回归，ovr和multinomial并没有任何区别，区别主要在多元逻辑回归上。
  • ovr不论是几元回归，都当成二元回归来处理。mvm从从多个类中每次选两个类进行二元回归。如果总共有T类，需要T(T-1)/2次分类。
  • OvR相对简单，但分类效果相对略差（大多数样本分布情况）。而MvM分类相对精确，但是分类速度没有OvR快。
  • 如果选择了ovr，则4种损失函数的优化方法liblinear，newton-cg,lbfgs和sag都可以选择。但是如果选择了multinomial,则只能选择newton-cg, lbfgs和sag了。
• class_weight=None : 类型权重参数。用于标示分类模型中各种类型的权重。默认不输入，即所有的分类的权重一样。
  • 选择‘balanced’自动根据y值计算类型权重。
  • 自己设置权重，格式：{class_label: weight}。例如0,1分类的er'yuan二元模型，设置class_weight={0:0.9, 1:0.1}，这样类型0的权重为90%，而类型1的权重为10%。
• random_state=None : 随机数种子，默认为无。仅在正则化优化算法为sag,liblinear时有用。
• max_iter=100 : 算法收敛的最大迭代次数。
• tol=0.0001 : 迭代终止判据的误差范围。
• verbose=0 : 日志冗长度int：冗长度；0：不输出训练过程；1：偶尔输出； >1：对每个子模型都输出
• warm_start=False : 是否热启动，如果是，则下一次训练是以追加树的形式进行（重新使用上一次的调用作为初始化）。布尔型，默认False。
• n_jobs=1 : 并行数，int：个数；-1：跟CPU核数一致；1:默认值。

LogisticRegression类的常用方法

• fit(X, y, sample_weight=None)
  • 拟合模型，用来训练LR分类器，其中X是训练样本，y是对应的标记向量
  • 返回对象，self。
• fit_transform(X, y=None, **fit_params)
  • fit与transform的结合，先fit后transform。返回X_new:numpy矩阵。
• predict(X)
  • 用来预测样本，也就是分类，X是测试集。返回array。
• predict_proba(X)
  • 输出分类概率。返回每种类别的概率，按照分类类别顺序给出。如果是多分类问题，multi_class="multinomial"，则会给出样本对于每种类别的概率。
  • 返回array-like。
• score(X, y, sample_weight=None)
  • 返回给定测试集合的平均准确率（mean accuracy），浮点型数值。
  • 对于多个分类返回，则返回每个类别的准确率组成的哈希矩阵。

示例

参考官网的例子，对鸢尾花数据进行逻辑回归。画图参考。

import numpy as np
from sklearn import linear_model, datasets
from sklearn.cross_validation import train_test_split

# 1.加载数据
iris = datasets.load_iris()
X = iris.data[:, :2]  # 使用前两个特征
Y = iris.target
#np.unique(Y)   # out: array([0, 1, 2])

# 2.拆分测试集、训练集。
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.3, random_state=0)
# 设置随机数种子，以便比较结果。

# 3.标准化特征值
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
sc.fit(X_train)
X_train_std = sc.transform(X_train)
X_test_std = sc.transform(X_test)

# 4. 训练逻辑回归模型
logreg = linear_model.LogisticRegression(C=1e5)
logreg.fit(X_train, Y_train)

# 5. 预测
prepro = logreg.predict_proba(X_test_std)
acc = logreg.score(X_test_std,Y_test)

因为这里数据量小，结果准确率只有0.7。嘛，只是小小的示范一下怎么使用sklearn的逻辑回归方法。在训练模型之前，可以优化一下模型参数，用GridSearchCV()函数。

---

参考文章：

• Logistic Regression 模型简介，美团技术，简单易懂。
• 逻辑回归模型(Logistic Regression, LR)基础
• 机器学习算法与Python实践之（七）逻辑回归（Logistic Regression）
• 对线性回归，logistic回归和一般回归的认识，斯坦福大学机器学习课程的笔记。
• 【机器学习算法系列之二】浅析Logistic Regression
• 逻辑回归算法的原理及实现(LR)，用Excel实现的。

---

1. 【机器学习算法系列之二】浅析Logistic Regression ↩

2. Cmd Markdown 公式指导手册 ↩

3. 78logistic 回归与线性回归的比较 ↩

4. 机器学习-损失函数 ↩

作者：ChZ_CC
链接：https://www.jianshu.com/p/e51e92a01a9c
來源：简书
简书著作权归作者所有，任何形式的转载都请联系作者获得授权并注明出处。