【机器学习】降维方法(二)----线性判别分析(LDA)

判别分析

首先了解了一下判别分析。
判别分析(Discriminant Analysis)是多元统计中用于判别样本所属类型的一种方法。通过训练已知分类类别的样本集来建立判别准则，然后用于判别新的预测样本的类别。

常用的判别分析方法有：

1.最大似然法：其基本思想为，通过训练样本集求出各种组合情况下该样本被分为任何一类的概率，确定参数。对于新样本的类别判别，只需要计算它被分到每一类中去的条件概率（似然值），选择概率最大的那一类为其分类。
回忆前面的朴素贝叶斯和逻辑回归的参数估计，都用到了最大似然的思想。 回 忆 前 面 的 朴 素 贝 叶 斯 和 逻 辑 回 归 的 参 数 估 计 ， 都 用 到 了 最 大 似 然 的 思 想 。
2.距离判别法：其基本思想是，由训练样本集得出每个分类的重心坐标，然后对待预测样本求出它们离各个类别重心的距离远近，从而归入离得最近的类。
和k均值的思路很像，不过k均值是聚类方法，它的训练样本集的分类类别 和 k 均 值 的 思 路 很 像 ， 不 过 k 均 值 是 聚 类 方 法 ， 它 的 训 练 样 本 集 的 分 类 类 别
未知，k就是我们需要设定的样本类别个数 未 知 ， k 就 是 我 们 需 要 设 定 的 样 本 类 别 个 数
3.Bayes判别法：其基本思想和最大似然法类似，不过最大似然法确定的是参数(点估计)，而贝叶斯会考虑到先验概率，且确定的是参数的分布(分布估计)。
4.Fisher判别法：也就是线性判别分析(LDA)，其基本思路就是投影。将原来在R维空间的样本投影到维度较低的D维空间去，然后在D维空间中再进行分类。投影的原则是使得每一类的差异尽可能小，而不同类间投影的离差尽可能大。
让我想起了一句话，低耦合高内聚hhh 让 我 想 起 了 一 句 话 ， 低 耦 合 高 内 聚 h h h
当分类只有两种且总体服从多元正态分布条件下，距离判别、Bayes判别与Fisher判别是等价的。

线性判别分析(LDA)

线性判别分析(Linear Discriminant Analysis)是一种经典的线性学习方法，是一种监督学习方法。将原来在R维空间的样本投影到维度较低的D维空间去，然后在D维空间中再进行分类。投影的原则是使得每一类的差异尽可能小，而不同类间投影的离差尽可能大。如下图(二分类二维示意图)：

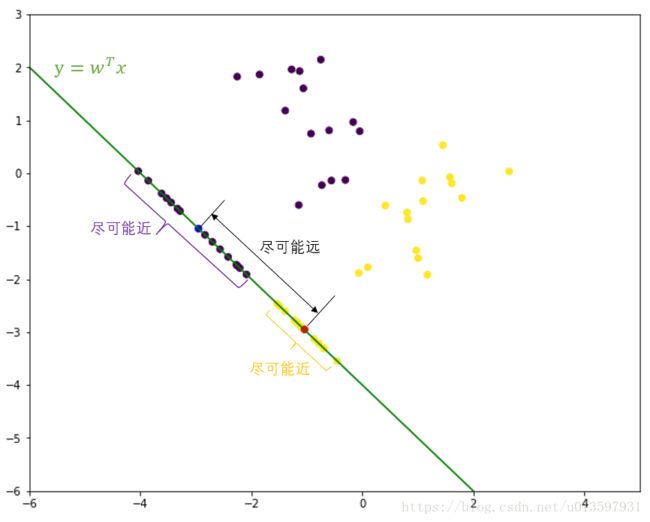
图中紫色点为0类样本，黄色点为1类样本，蓝色点为0类样本投影点均值，红色为1类样本投影点均值。
给定训练数据集 D={(x1,y1),(x2,y2),...,(xm,ym)} D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x m , y m ) } ， xi∈{x(1)i,x(2)i,...,x(n)i} x i ∈ { x i ( 1 ) , x i ( 2 ) , . . . , x i ( n ) } ， yi∈{0,1} y i ∈ { 0 , 1 } ， Xi X i 表示属于第 i i 类的样本的集合。

二分类问题：

此处我们讨论的是二分类问题 此 处 我 们 讨 论 的 是 二 分 类 问 题
0类样本均值 μ0 μ 0 :
μ0=1k0∑x∈X0xi μ 0 = 1 k 0 ∑ x ∈ X 0 x i ， k0 k 0 为0类的样本数量。
投影后为：wTμ0 投 影 后 为 ： w T μ 0

1类样本均值 μ1 μ 1 :
μ1=1k1∑x∈X1xi μ 1 = 1 k 1 ∑ x ∈ X 1 x i ， k1 k 1 为1类的样本数量。
投影后为：wTμ1 投 影 后 为 ： w T μ 1

0类样本协方差矩阵 ∑0 ∑ 0 :
∑0=∑x∈X0(xi−μ0)(xi−μ0)T ∑ 0 = ∑ x ∈ X 0 ( x i − μ 0 ) ( x i − μ 0 ) T
投影后为：wT∑0w 投 影 后 为 ： w T ∑ 0 w

1类样本协方差矩阵 ∑1 ∑ 1 :
∑1=∑x∈X1(xi−μ1)(xi−μ1)T ∑ 1 = ∑ x ∈ X 1 ( x i − μ 1 ) ( x i − μ 1 ) T
投影后为：wT∑1w 投 影 后 为 ： w T ∑ 1 w

类的协方差矩阵越小，表示这个类中的样本越聚集于这个类的均值点。我们希望这些同类样本的投影点尽可能的近，即 wT∑0w+wT∑1w w T ∑ 0 w + w T ∑ 1 w 尽可能的小。
类内散度矩阵：Sw=∑0+∑1 类 内 散 度 矩 阵 ： S w = ∑ 0 + ∑ 1
对于类的均值的投影点，我们用 ||wTμ0−wTμ1||22 | | w T μ 0 − w T μ 1 | | 2 2 表示它们之间的距离。我们希望这个距离尽可能的大。
类间散度矩阵：Sb=(μ0−μ1)(μ0−μ1)T 类 间 散 度 矩 阵 ： S b = ( μ 0 − μ 1 ) ( μ 0 − μ 1 ) T
同时考虑这两者，我们希望最大化 J(w) J ( w )
J(w)=||wTμ0−wTμ1||22wT∑0w+wT∑1w=wT(μ0−μ1)(μ0−μ1)TwwT(∑0+∑1)w=wTSbwwTSww J ( w ) = | | w T μ 0 − w T μ 1 | | 2 2 w T ∑ 0 w + w T ∑ 1 w = w T ( μ 0 − μ 1 ) ( μ 0 − μ 1 ) T w w T ( ∑ 0 + ∑ 1 ) w = w T S b w w T S w w
为了解这个公式，需要观察这个式子，可以发现上下都有 w w 的二次项，因此 J(w) J ( w ) 的解与 w w 的长度无关(即 ||w|| | | w | | 被上下抵消，不会影响 J(w) J ( w ) 的解，但是w的方向会影响到 J(w) J ( w ) )
对于 J(w) J ( w ) 分子分母都可以取任意值(比如若 w w 是一个解，则对于任意常数α，αw也是解)，这样会得到无穷个解，因此我们限制 wTSww=1 w T S w w = 1 ，则最大化 J(w) J ( w ) 转换为了这样一个问题：
　　　　 maxw　wTSbw max w 　 w T S b w
　　　　 s.t.　wTSww=1 s . t . 　 w T S w w = 1
等价于：
　　　　 minw　−wTSbw min w 　 − w T S b w
　　　　 s.t.　wTSww=1 s . t . 　 w T S w w = 1
对于这种问题，似曾相识，可以用拉格朗日乘子法将约束项和优化问题放在一个式子内，令 L(w,λ)=−wTSbw+λ(wTSww−1) L ( w , λ ) = − w T S b w + λ ( w T S w w − 1 )
求导令 ∂L(w,λ)∂w=−2Sbw+2λSww=0 ∂ L ( w , λ ) ∂ w = − 2 S b w + 2 λ S w w = 0
得 λSww=Sbw λ S w w = S b w ，由于 Sbw S b w 的方向恒为 μ0−μ1 μ 0 − μ 1 ，所以可以写为 Sbw=β(μ0−μ1)=λ(μ0−μ1) S b w = β ( μ 0 − μ 1 ) = λ ( μ 0 − μ 1 )
(μ0−μ1)Tw是标量，因此Sbw=(μ0−μ1)(μ0−μ1)Tw ( μ 0 − μ 1 ) T w 是 标 量 ， 因 此 S b w = ( μ 0 − μ 1 ) ( μ 0 − μ 1 ) T w
=β(μ0−μ1)，又由于若w是一个解，则对于任意常数α， = β ( μ 0 − μ 1 ) ， 又 由 于 若 w 是 一 个 解 ， 则 对 于 任 意 常 数 α ，
αw也是解，因此Sbw=λβSbw=λ(μ0−μ1) α w 也 是 解 ， 因 此 S b w = λ β S b w = λ ( μ 0 − μ 1 )
因此可得 λSww=λ(μ0−μ1) λ S w w = λ ( μ 0 − μ 1 ) ， w=S−1w(μ0−μ1) w = S w − 1 ( μ 0 − μ 1 ) ，然后再对 Sw S w 进行奇异值分解，得出 S−1w S w − 1

多分类问题：

将LDA推广到多分类问题。假设存在N个类，第 i i 个类的样本数为 mi m i ，所有样本数为 m m 。
全部样本均值 μ μ ：
μ=1m∑i=1mxi μ = 1 m ∑ i = 1 m x i
第i个类的样本均值 μi μ i ：
μi=1mi∑x∈Xix μ i = 1 m i ∑ x ∈ X i x
全局散度矩阵 St S t ：
St=Sb+Sw=∑i=1m(xi−μ)(xi−μ)T S t = S b + S w = ∑ i = 1 m ( x i − μ ) ( x i − μ ) T
也就是对所有的样本点求协方差得到一个协方差矩阵 也 就 是 对 所 有 的 样 本 点 求 协 方 差 得 到 一 个 协 方 差 矩 阵
第i个类的散度矩阵 Swi S w i ：
Swi=∑x∈Xi(x−μi)(x−μi)T S w i = ∑ x ∈ X i ( x − μ i ) ( x − μ i ) T
类内散度矩阵 Sw S w ：
Sw=∑i=1NSwi S w = ∑ i = 1 N S w i
也就是所有类别的散度矩阵(协方差矩阵)之和 也 就 是 所 有 类 别 的 散 度 矩 阵 ( 协 方 差 矩 阵 ) 之 和
类间散度矩阵 Sb S b ：
Sb=St−Sw=∑i=1Nmi(μi−μ)(μi−μ)T S b = S t − S w = ∑ i = 1 N m i ( μ i − μ ) ( μ i − μ ) T
推导如下：
Sb=St−Sw S b = S t − S w
=∑i=1m(xi−μ)(xi−μ)T−∑i=1N∑x∈Xi(x−μi)(x−μi)T = ∑ i = 1 m ( x i − μ ) ( x i − μ ) T − ∑ i = 1 N ∑ x ∈ X i ( x − μ i ) ( x − μ i ) T
=∑i=1N∑x∈Xi(x−μ)(x−μ)T−∑i=1N∑x∈Xi(x−μi)(x−μi)T = ∑ i = 1 N ∑ x ∈ X i ( x − μ ) ( x − μ ) T − ∑ i = 1 N ∑ x ∈ X i ( x − μ i ) ( x − μ i ) T
=∑i=1N∑x∈Xi[(x−μ)(x−μ)T−(x−μi)(x−μi)T] = ∑ i = 1 N ∑ x ∈ X i [ ( x − μ ) ( x − μ ) T − ( x − μ i ) ( x − μ i ) T ]
=∑i=1N∑x∈Xi[(x−μ)(xT−μT)−(x−μi)(xT−μTi)] = ∑ i = 1 N ∑ x ∈ X i [ ( x − μ ) ( x T − μ T ) − ( x − μ i ) ( x T − μ i T ) ]
=∑i=1N∑x∈Xi(xxT−μxT−xμT+μμT−xxT+μixT+xμTi−μiμTi) = ∑ i = 1 N ∑ x ∈ X i ( x x T − μ x T − x μ T + μ μ T − x x T + μ i x T + x μ i T − μ i μ i T )
=∑i=1N∑x∈Xi[(μi−μ)xT+(μTi−μT)x+μμT−μiμTi] = ∑ i = 1 N ∑ x ∈ X i [ ( μ i − μ ) x T + ( μ i T − μ T ) x + μ μ T − μ i μ i T ]
因为μi=1mi∑x∈Xix，所以∑x∈Xix=miμi 因 为 μ i = 1 m i ∑ x ∈ X i x ， 所 以 ∑ x ∈ X i x = m i μ i
=∑i=1N[(μi−μ)miμTi+(μTi−μT)miμi+miμμT−miμiμTi] = ∑ i = 1 N [ ( μ i − μ ) m i μ i T + ( μ i T − μ T ) m i μ i + m i μ μ T − m i μ i μ i T ]
=∑i=1N[mi(μiμTi−μμTi+μTiμi−μTμi+μμT−μiμTi)] = ∑ i = 1 N [ m i ( μ i μ i T − μ μ i T + μ i T μ i − μ T μ i + μ μ T − μ i μ i T ) ]
=∑i=1N[mi(−μμTi+μTiμi−μTμi+μμT)] = ∑ i = 1 N [ m i ( − μ μ i T + μ i T μ i − μ T μ i + μ μ T ) ]
=∑i=1N[mi(μi−μ)(μi−μ)T] = ∑ i = 1 N [ m i ( μ i − μ ) ( μ i − μ ) T ]

由上我们可以看出，任意求得 St S t 、 Sw S w 、 Sb S b 三者中任意两个都可以根据得到的两个求出第三个。

常见实现方法如下，优化目标为(找到 W W 使得 WTSbW W T S b W 的迹与 WTSwW W T S w W 的迹之商最大)：
　　　 maxWtr(WTSbW)tr(WTSwW)=∏i=1kwTiSbwi∏i=1kwTiSwwi max W t r ( W T S b W ) t r ( W T S w W ) = ∏ i = 1 k w i T S b w i ∏ i = 1 k w i T S w w i
其中 W∈Rk×(N−1) W ∈ R k × ( N − 1 )
这里用迹是因为WTSbW和WTSwW是矩阵不是标量 这 里 用 迹 是 因 为 W T S b W 和 W T S w W 是 矩 阵 不 是 标 量
求解 W W ， W W 的闭式解就是 S−1wSb S w − 1 S b 的前 k k 个最大非零广义特征值所对应的特征向量组成的矩阵， k≤N−1 k ≤ N − 1
也就是对S−1wSb进行特征值分解，找到前k个最大的特征值 也 就 是 对 S w − 1 S b 进 行 特 征 值 分 解 ， 找 到 前 k 个 最 大 的 特 征 值

可以将 W W 视为一个投影矩阵，则多分类LDA将样本投影到 k k 维空间，且在投影过程中使用了类别信息(PCA在投影过程中并未考虑类别信息)

LDA优缺点：

LDA算法的主要优点有：
1.在降维过程中可以使用类别的先验知识经验；
2.LDA在样本分类信息依赖均值而不是方差的时候，降维效果较好。

LDA算法的主要缺点有：
1.LDA不适合对非高斯分布样本进行降维；
2.LDA降维最多降到类别数k-1的维数，如果我们降维的维度大于k-1，则不能使用LDA；
3.LDA在样本分类信息依赖方差而不是均值的时候，降维效果不好；
4.LDA可能过度拟合数据。

参考：
1.《机器学习》3.4线性判别分析—-周志华
2. http://blog.jobbole.com/88195/
3. http://www.cnblogs.com/pinard/p/6244265.html