【西瓜书阅读笔记】第7章 贝叶斯分类器
第7章 贝叶斯分类器
- 7.1 贝叶斯决策论
- 7.2 极大似然估计MLE
- 7.3 朴素贝叶斯分类器
- 西瓜好坏实例
- 7.4 半朴素贝叶斯分类器
- 7.5 贝叶斯网
- 7.5.1 结构
- 7.5.2 学习
- 7.5.3 推断
- 7.6 EM算法
7.1 贝叶斯决策论
在概率框架下决策
下面以多分类为例
期望损失(或称为风险):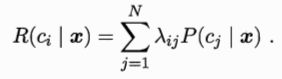
判定准则:最小化总体风险
贝叶斯判定准则:为最小化总体风险,只需在每个样本上选择哪个能使条件风险最小的类别标记
贝叶斯最优分类器:
贝叶斯风险:
想要用贝叶斯判定准则来最小化决策风险,首先要获得后验概率。
由于后验概率实际上难以获取,机器学习任务是:基于有限的训练样本集,来估计后验概率。
大概有2中策略:
1.判别式模型
2.生成式模型
估计后验概率的问题,转化为:基于训练数据来估计先验概率和条件概率
对类先验概率:根据大数定律,可以通过各类样本出现的频率来估计
对类条件概率:由于涉及x所有属性的联合概率,根据样本直接估计较困难,有些样本根本没出现,不可行。
7.2 极大似然估计MLE
估计类条件概率的策略:
1.假定某种确定的概率分布形式
2.参数估计
(概率模型的训练过程,就是参数估计的过程)
两种学派的两种不同方案:
1.频率主义学派:参数客观存在固定值,通过优化似然函数等准则来确定参数值——极大似然估计MLE
2.贝叶斯学派:参数本身也有分布,先假定参数服从一个先验分布,然后计算后验分布
寻找一个参数,使得样本出现的概率最大
缺点:对假设的概率分布形式依赖性很大,很难找到分布,只能靠经验假设
7.3 朴素贝叶斯分类器
用贝叶斯公式来估计后验概率,有困难:类条件概率是多有属性上的联合概率,很难从样本直接估计
为了解决上述困难,朴素贝叶斯分类器采用了:属性条件独立性假设:对已知类别,所有属性互相独立
朴素贝叶斯分类器,训练过程:基于训练集来估计类先验概率,并为每个属性估计条件概率。
西瓜好坏实例
步骤:
- 估计类先验概率
- 为每个属性估计条件概率
- 全部概率相乘,看看好瓜,坏瓜出现的概率
- 谁概率大,就分为谁的类
缺点:若某个属性从没有与某一类出现过,就不太合理

为了避免这种情况(避免某一属性被“抹去”):估计概率值时需要:平滑
平滑常用方法:拉普拉斯修正


贝叶斯分类器在现实任务中有多种方式:
- 对预测速度要求较高时:将所有概率估计先算好存起来,预测时查表
- 任务数据更替频繁:懒惰学习,先不进行训练,等需要测试时再训练
- 数据不断增加:在现有的估值基础上,对新增样本所涉及的属性进行修正即可
7.4 半朴素贝叶斯分类器
因为朴素贝叶斯分类器采用的是属性条件独立性假设,其实这个假设也很难成立。
只好对属性独立性假设进行一定程度的放松==>半朴素贝叶斯分类器
基本想法:适当地考虑一部分属性间的依赖关系
常用策略:独依赖估计ODE
关键问题转变成:确定每个属性的父属性
最直接的方法:假设所有属性都依赖同一个属性(称为超父),然后通过交叉验证等模型来确定这个超父是谁(叫做SPODE方法)
TAN:在最大带权生成树的基础上,通过某些步骤将属性间依赖关系简约成一种树形结构(步骤跳过!)【保留了强相关属性之间的依赖性】
AODE:是一种集成学习机制、更为强大的独依赖分类器。(步骤跳过!)【通过预计算节省预测时间,也能懒惰学习(预测时再计数),易于实现增量学习】
7.5 贝叶斯网
也称“信念网”,用有向无环图(DAG)来刻画属性之间的依赖关系,并使用条件概率表(CPT)来描述属性的联合概率分布
7.5.1 结构
三种典型关系:同父、V型(也称冲撞)【边际独立性】、顺序

有向分离:分析有向图中变量间的条件独立性
先把有向图转变为==》无向图(这种生成的图叫道德图):
1.把V型结构的父节点相连
2.把有向边改成无向边
基于道德图能直观、迅速地找到变量间的条件独立性
7.5.2 学习
已知网络结构,学习过程就比较简单:
对训练样本进行“计数”,估计每个结点的条件概率表。
事实上,我们根本不知道网络结构,所以,贝叶斯网学习的首要任务:根据训练集构造贝叶斯网。
常用方法:评分搜索:
1.定义一个评分函数(用于评估贝叶斯网与训练集的契合程度)
2.基于这个评分函数,寻找最优贝叶斯网
常用的评分函数:基于信息论准则
最小描述长度准则(MDL):选择综合编码长度最短的贝叶斯网络(压缩任务)
缺点:从所有可能的网络结构空间搜索最优贝叶斯网是一个NP难问题,难以快速求解
两种方法加快:
1.贪心法:不断调整边,使得评分函数不再降低为止
2.施加约束:例如将网络限制为树型
7.5.3 推断
训练好的贝叶斯网络,可用于:查询
“精确推断”是NP难问题,需要借助“近似推断”降低精度要求
常用方法:吉布斯采样(一种随机采样方法)(跳过!)
7.6 EM算法
有时候训练样本不完整(某些属性值未知,叫做隐变量)
估计隐变量的常用利器:EM算法
(跳过!睡觉去了~)