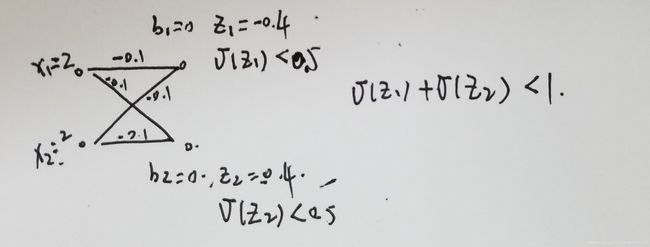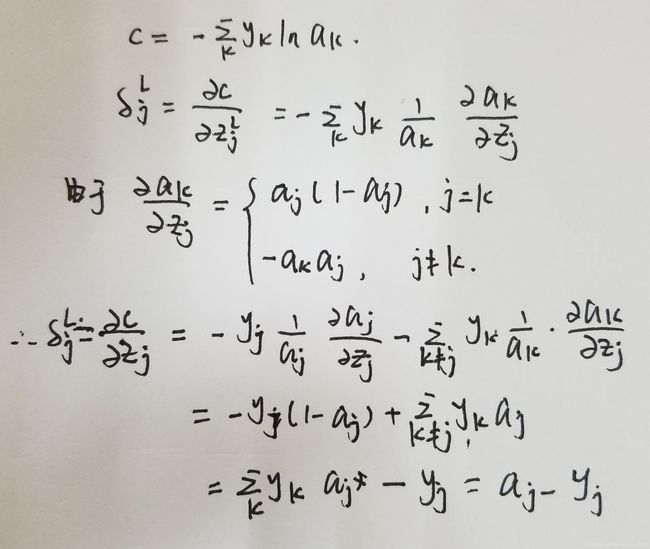Neural Networks and Deep Learning习题解答--改进神经网络的学习方法

神经网络与深度学习习题解答

改进神经网络的学习方法

最近在看 Michael Nielsen的Neural Networks and Deep Learning，这本书是以网页的形式放在网上，非常合适入门，附上传送地址：http://neuralnetworksanddeeplearning.com/chap1.html#learning_with_gradient_descent

国内哈工大社会计算与信息检索研究中心将这本书翻译成中文版放在网络上，地址为：https://hit-scir.gitbooks.io/neural-networks-and-deep-learning-zh_cn/content/chap1/c1s5.html

该章详细介绍交叉熵正则化等一系列可以对神经网络做改进的技巧和方法。下面给出该章习题

交叉熵部分

1. 证明σ′(z)=σ(z)(1−σ(z))。

2. 交叉熵带来的一个问题就是很难记住表达式中y和a的位置。我们很容易记不清正确的表达式是−[ylna+(1−y)ln(1−a)]还是−[alny+(1−a)ln(1−y)]。当y=0或1时，如果使用了第二个表达式会发生什么呢？这个问题会发生在第一个表达式上吗？请说明你的理由。

3. 在本节开始讨论单个神经元时，我曾声称如果所有的训练数据都有σ(z)≈y，那么交叉熵会变得非常小。这个假设依赖于y非0即1。这对于分类问题是正确的，但是对于其他问题（比如回归问题）y的取值可能在0和1之间。证明当所有的训练数据σ(z)=y时，交叉熵仍然是最小化的。
4. 我们已经详尽地讨论了当我们使用平方代价来训练的神经网络时，会产生输出神经元饱和、学习速率下降的问题。另一个会妨碍学习的因素是等式（61）中xj项。因为该项的存在，当输入xj接近于0时，对应的权重wj会学习得很慢。解释一下，为什么我们不能通过选择一个好的代价函数来消除xj项。

1. 高中导数知识

 图（1）

2. 这里注意y=0或者1，而激活值a一般只可能接近0或1。对于−[alny+(1−a)ln(1−y)]，式子本身就不成立，lny在y=0处并没有定义，及时按照无限接近这样的思想来处理，lny在y=0处也趋近于无穷大，而a是一个比较小的定值，使得和的第一项趋近于无穷大，而和的第二项的ln(1-y)在y=0的时候为0，因而代价函数无穷大，这显然不是理想的结果。用−[ylna+(1−y)ln(1−a)]公式就没有这样的结果，因为y不是0就是1，整个代价函数也在0~1范围内并接近0。

3. 这个证明俨然一个导数的高考题啊，证明也比较简单。

图（2）
4.代价函数对权重的偏导和代价函数对偏置的偏导分别如下：

假设可以通过选择一个合适的代价函数来消除 xj 项，此时对于同一个输出， 、...的计算结果均一致，甚至的变化率也和权重变化率一致，此时整个网络的所有参数将保持一致的变化率和变化趋势，这显然不符合神经网络更新权重的理想结果，也难以达到理想的目标。所以不可通过一个合适好的代价函数来消除 xj 项。

softmax

网上关于softmax有一个很好的图来表示。带有softmax层的神经网络，每个神经元的输出均与所有的带权输入有关。

 图 (*)

练习有如下：

1. 构造例子说明在使用 sigmoid 输出层的网络中，输出激活值aLj的和并不一定为1
2. softmax 的单调性 - 证明如果j=k，那么∂aLj/∂zLk是正的，如果j≠k，则是负的。如果我们增加zjL能够保证增加相应的输出激活值ajL，同时会减少其它所有的输出激活值，我们已经通过滑块清楚地看到这个结论，但是现在需要一个严格的证明。
3. softmax 的非局部性 - sigmoid 层的一个好处是输出aLj是其对应输入的一个函数aLj=σ(zLj)。解释一下为什么对于 softmax 层并不是这样的情况：任何一个输出激活值aLj依赖于所有的输入。
4. 反转 softmax 层 - 假设我们有一个带有 softmax 输出层的神经网络，同时已知激活值ajL。证明对应的带权输入的形式为zLj=lnaLj+C，其中常数C是不依赖于j的。
5. 推导等式（81）和（82），等式见下图。
6. 「softmax」这个名字来源于哪里？假设我们改变一下 softmax 函数，使得输出激活值式（83），其中c是一个正常数。注意c=1对应到标准的 softmax 函数。但是如果我们使用不同的c，我们会得到不同的函数，尽管如此，最后得到的结果也和 softmax 很相似。证明改变c以后，也会像通常的 softmax 函数一样形成一个概率分布。假设我们允许c非常大，比如c→∞，那么输出激活值ajL的极限是什么？
7. 证明表达式（84）。

1. 这样的例子很多，下面给出一个简单的例子。我们也可以这么假设，假设某种情况下满足激活值的和为1，那么此时调整其中一个神经元的偏置，该神经元的激活值就会改变，输出层激活值的和显然不为1了。

图（3）

2. 按部就班求导就行。这里注意指数函数本身大于0的性质。

图（4）

3. 见上文的图(*)，显然softmax层的每个神经元的输出公式里包含了所有的带权输入。

4. 证明如下，因为已知激活值ajL，所以等式右边 ln 的那个式子是比依赖于 j 的常数，即为题目中所述的C。

图（5）

5. 在很多资料中，神经网络中的log和ln似乎没有区分，计算均作为ln计算，求导都是倒数。该题求解见下图。其中参考了

https://blog.csdn.net/u014313009/article/details/51045303。这里表达式C写成累加和的形式是因为yi代表真实值，如果只预测一个结果，那个yi只有一种情况为1，所有表达式简写为 C = -ykln(ak)，其中k是正确输出的结果。一般yk=1,那么就写成 C= -lna,即书中的形式。是不是感觉这里与交叉熵非常相似，书中明明说的是对log似然，或者说对数似然，但是这里却和交叉熵公式一致，我也有这样的困惑。查阅资料后，得知对数似然代价函数在多分类时可以化简为交叉熵代价函数的形式。来源为https://juejin.im/post/5b38971be51d4558b10aad26#heading-11

图（6）

6. softmax在有的译本中被翻译为柔性最大值，这里的柔性和变化率有关。图（4）已经给出了激活函数对于带权输入的偏导数，这也被直接用于图（6）中代价函数关于权重和偏置的变化率的证明中。对于式（83），因为多了c，该式求导后将要多出系数c，当c趋近于无穷，权重和偏置的变化率将非常大，c=1的时候变化率最小，可以认为使得函数变化变得柔和很多。

7. 这个证明和图（6）中的证明方法和过程均一致，emm就是一样的。不过这里还是写下

 本章到该部分为止讲了交叉熵和softmax的原理和一些公式原理的推导和证明。这里注意两个组合，sigmoid激活函数和交叉熵代价函数的组合，以及softmax和log-likelihood （对数似然）代价函数的组合，两个组合都能有效解决学习速度下降的问题。关于二分类中交叉熵函数和log似然函数的总结，其他博客给出了比较好的解释

注意到不管是交叉熵损失函数与 log 似然损失函数，交叉熵损失函数用于二分类问题， log 似然损失函数用于多分类，但是对于某一个样本只属于一个类别，只有一个标签。如果用 one-hot 编码样本的标签那么，对于标签向量只有一个分量的值为 1 其余的值都为 0。

所以不管是交叉熵损失函数与 log 似然损失函数，都可以化简为：

其中，  是向量   中取值为 1 对应的第  个分量的值。在这里本质上是一样的。作者建议采用 Kears 中的命名方法，对于二分类的交叉熵损失函数称之为 “二分类交叉熵损失函数（binary_crossentropy）” ，对于多分类的交叉熵损失函数称之为 “多类别交叉熵损失函数（categorical_crossentropy）”。
来源链接：https://juejin.im/post/5b38971be51d4558b10aad26

权重初始化

1. 验证z = sum(wx)+b标准差为sqrt(3/2)。下面两点可能会有帮助：（a）独立随机变量和的方差，是每个独立随机变量方差的和；（b）方差是标准差的平方。

1. 权重初始化目的是为了让每一层的输出z(神经元前的那一项)和该层输出 x 保持一致的数据分布。权重初始化的方法是对权重的数据除以输入权重神经元个数的根号，即通过w=np.random.randn(n)/sqrt(n)来初始化。这个题目的证明需要注意 w 和 x 和 b 三个变量相互独立。过程见下图

其他改进神经网络方法的技术

该节主要介绍了momentum及人工神经元的其他模型。momentum的公式如下，该方法引入了一个称为速度(velocity)的概念，梯度的作用是改变速度，而不是直接改变位置，另外，momentum方法引入了一种摩擦力的项，用来逐渐减少速度。如书中所述，这里需要注意变量之间的对应关系，速度变量 v = v1,v2,v3...其中每一个对应wj变量，我理解这里的 v 和 w 是维度和大小(shape)是一样的，即每个Wij都对应一个vij。

1. 如果我们使⽤ µ > 1 会有什么问题？ • 如果我们使⽤ µ < 0 会有什么问题？
2. 增加基于 momentum 的随机梯度下降到 network2.py 中。
3. 证明公式 (111)

1. 这个µ类似于物理中的摩擦力，这里用来约束v的变化，µ=1时，没有摩擦，速度由▽C决定，速度每次都在叠加，梯度下降的速度将比正常的梯度下降速度快很多；µ=0时，存在很大的摩擦，速度无法叠加，这个时候就等同于通常所说的梯度下降。在实践中，使用0和1之间的µ值可以为我们避免过量而又能够叠加速度的好处。

那么 µ > 1或者 µ < 0有什么问题呢，显然，作为摩擦力来理解的话，µ > 1就是凭空出现v的叠加，可以理解在完全光滑的平面上一个物体不受外力作用速度却在增加，这就使得梯度下降几乎不受控制一直增大，及时▽C反向也不能阻止w向一个方向更新，最后w越来越大，越来越大(或者越来越小)...效果在达到最优之后越过，从而越来越差。当µ < 0时，可以认为摩擦力太大，大到摩擦力竟然比物体本身的重量还要大,相当于给物体一个额外的向下的压力，此时，参数更新不是叠加地增加了，是叠加的减少，即梯度下降一开始朝一个方向，但momentum 会使得梯度下降比常规的梯度下降更慢，甚者，在▽C最小（约为0），即达到最优的时候，权重开始反向改变，始终无法停留在最优处。

2. 根据公式感觉这个代码还是比较好改的，真正改的时候对于变量的类型和维度还是要考虑一些地方。如下在 update_mini_batch函数的参数更新的地方做了修改。

    def update_mini_batch(self, mini_batch, eta, lmbda, n, momentum):
        nabla_b = [np.zeros(b.shape) for b in self.biases]
        nabla_w = [np.zeros(w.shape) for w in self.weights]
        for x, y in mini_batch:
            delta_nabla_b, delta_nabla_w = self.backprop(x, y)
            nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
            nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]

        # 原方法Stochastic Gradient Descent(Mini-Batch SGD)
        # self.weights = [(1-eta*(lmbda/n))*w-(eta/len(mini_batch))*nw
        #                 for w, nw in zip(self.weights, nabla_w)]
        # self.biases = [b-(eta/len(mini_batch))*nb
        #                for b, nb in zip(self.biases, nabla_b)]
        # Momentum-SGD 下降法
        vss = [momentum*vs - (eta/len(mini_batch))*nw
                        for vs, w, nw in zip(self.vs, self.weights, nabla_w)]
        self.weights = [w + vs
                        for vs, w, nw in zip(vss, self.weights, nabla_w)]
        self.biases = [b-(eta/len(mini_batch))*nb
                       for b, nb in zip(self.biases, nabla_b)]

注意这里多了 momentum以及self.vs，前者传递的是公式(107)的µ，后者存储的是公式(107)的v。这里的self.vs和self.weights存储类型一致，其为list类型，list的每个元素是一个矩阵，存储的是每个权重wij的变化速率。而该速率初始化为0，因而default_weight_initializer函数也加了self.vs的初始化。

    def default_weight_initializer(self):
        # 默认使用新的权重初始化方法进行初始化
        self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]]
        self.weights = [np.random.randn(y, x)/np.sqrt(x)
                        for x, y in zip(self.sizes[:-1], self.sizes[1:])]
        self.vs = [np.zeros([y, x])
                        for x, y in zip(self.sizes[:-1], self.sizes[1:])]

之后记得在SGD函数和update_mini_batch函数的参数传递里加上momentum就行了。另外，我这样的修改方法没有考虑到正则化，如果需要还需要另行添加。

3. 公式证明比较简单