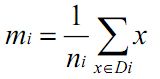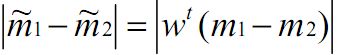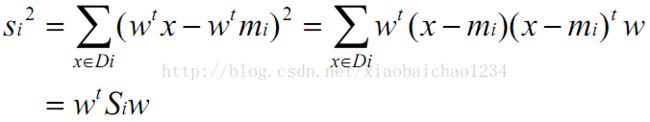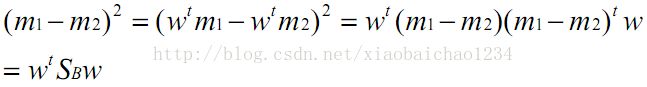- There was a problem confirming the ssl certificate: [SSL:CERTIFICATE_ VERIFY_ FAILED]certificate解决方案
爱编程的喵喵
Python基础课程pythonpipSSLcertificate解决方案
大家好,我是爱编程的喵喵。双985硕士毕业,现担任全栈工程师一职,热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。现为CSDN博客专家、人工智能领域优质创作者。喜欢通过博客创作的方式对所学的知识进行总结与归纳,不仅形成深入且独到的理解,而且能够帮助新手快速入门。 本文主要介绍了Therewasaproblemco
- 使用 Python 和 scikit-learn 实现 KNN 分类:以鸢尾花数据集为例
弥树子
pythonscikit-learn分类
在机器学习的世界里,K-NearestNeighbors(KNN)算法是一种简单而强大的分类方法。它基于一个直观的想法:相似的数据点往往属于同一类别。本文将通过Python的scikit-learn库实现KNN分类,以经典的鸢尾花数据集为例,展示从数据加载到模型评估的完整流程。1.KNN算法简介KNN是一种监督学习算法,主要用于分类和回归任务。它的工作原理非常简单:对于一个新的数据点,算法会查找训
- git clone出现fatal: unable to access Failed to connect to github.com port 443: Timed out解决方案
爱编程的喵喵
Python基础课程gitgithubtimeoutport443解决方案
大家好,我是爱编程的喵喵。双985硕士毕业,现担任全栈工程师一职,热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。现为CSDN博客专家、人工智能领域优质创作者。喜欢通过博客创作的方式对所学的知识进行总结与归纳,不仅形成深入且独到的理解,而且能够帮助新手快速入门。 本文主要介绍了gitclone出现fatal:un
- Gradio 快速构建机器学习web可视化界面心得
算法小菜鸟成长心得
python
1.操作完成提示try:#对输入的字符串代码进行编译运行exec(get_test_code_example)gr.Info("Modeltestingcompletedsuccessfully.")except:raisegr.Error("Modeltestingfailed.")用到了gr.Info()和gr.Errot()
- linux git clone出现fatal: unable to access Failed to connect to github.com port 443: Timed out解决方案
herosunly
C/C++/Linux解决方案linuxgitgithubtimeoutport443
大家好,我是herosunly。985院校硕士毕业,现担任算法研究员一职,热衷于机器学习算法研究与应用。曾获得阿里云天池比赛第一名,CCF比赛第二名,科大讯飞比赛第三名。拥有多项发明专利。对机器学习和深度学习拥有自己独到的见解。曾经辅导过若干个非计算机专业的学生进入到算法行业就业。希望和大家一起成长进步。 本文主要介绍了linuxgitclone出现fatal:unabletoaccessF
- flask+layui学生信息管理系统
元宇宙中的程序员
flasklayuipython
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档文章目录前言一、pandas是什么?二、使用步骤1.引入库2.读入数据总结前言提示:这里可以添加本文要记录的大概内容:例如:随着人工智能的不断发展,机器学习这门技术也越来越重要,很多人都开启了学习机器学习,本文就介绍了机器学习的基础内容。一、数据库建模1、创建数据模型classStudentORM(db.Model):stu_id=d
- Python 3.9它来啦!!!
python程序员小'鹏
python编程语言经验分享程序人生
Python3.9,来了!小编本身就是一名python开发工程师,我自己花了三天时间整理了一套python学习教程,从最基础的python脚本到web开发,爬虫,数据分析,数据可视化,机器学习,等,这些资料有想要的小伙伴"点击"即可领取过去一年,来自世界各地的开发者们一直在致力于Python3.8的改进。Python3.9beta版本已经存在了一段时间,第一个正式版本于2020年10月5日发布。每
- AI智能制造软件有什么用处
雪叶雨林
行业资讯AI人工智能制造
随着信息技术与制造业的深度融合,人工智能(AI)逐渐成为提升制造效率和灵活性的重要工具。AI智能制造软件通过集成数据分析、机器学习和自动化流程,为企业提供了优化生产、降低成本和提高质量的新途径。生产过程优化实时监控与反馈AI智能制造软件能够实时收集生产线上的各类数据,如温度、压力、速度等参数,并通过机器学习算法进行分析处理。一旦检测到异常情况,系统会立即发出警报并提供改进建议,帮助企业快速响应问题
- ModuleNotFoundError: No module named ‘pywin32_bootstrap‘解决方案
爱编程的喵喵
Python基础课程pythonModuleNotFoundwin32_bootstap解决方案
大家好,我是爱编程的喵喵。双985硕士毕业,现担任全栈工程师一职,热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。现为CSDN博客专家、人工智能领域优质创作者。喜欢通过博客创作的方式对所学的知识进行总结与归纳,不仅形成深入且独到的理解,而且能够帮助新手快速入门。 本文主要介绍了ModuleNotFoundErro
- 人脸识别的经典深度学习方法
明初啥都能学会
深度学习人工智能
人脸识别的经典深度学习方法引言1.卷积神经网络(CNN)1.1LeNet1.2AlexNet1.3VGGNet1.4ResNet2.人脸检测2.1Viola-Jones算法2.2基于深度学习的人脸检测3.人脸特征提取3.1主成分分析(PCA)3.2人脸对齐3.2.1基于特征点的对齐3.2.2基于深度学习的对齐4.人脸识别模型4.1传统机器学习方法4.2基于深度学习的方法5.公式解读5.1卷积运算5
- AI智能获客工具的意义是什么
雪叶雨林
AI行业资讯人工智能
在当今竞争激烈的市场环境中,企业需要高效、精准的获客策略来维持增长和竞争力。AI智能获客工具的出现,为企业提供了一种全新的解决方案,通过自动化和智能化手段提高获客效率和质量。一、AI智能获客工具的核心价值1.1提高获客效率AI智能获客工具通过自动化流程,如自动筛选潜在客户、自动发送营销信息等,大幅减少了人力投入和时间成本,从而提高了获客效率。1.2精准定位潜在客户利用机器学习和大数据分析技术,AI
- MicroAI™将人工智能培训引入RENESAS MCU
sinat_41698914
人工智能mcubigdata
在端点部署的人工智能技术将加快资产密集型行业的上市时间达拉斯--(美国商业资讯)--边缘原生人工智能(AI)和机器学习(ML)产品领域的先驱MicroAITM今天宣布,公司已将其MicroAIAtomML™技术与RenesasRA微控制器(MCU)产品线进行整合。与全球微控制器领导者Renesas合作将机器学习引入MCU,并借助MicroAI直接在嵌入式环境中训练机器学习模型的能力——这在业界尚属
- C++ 与机器学习:构建高效推理引擎的秘诀
salsm
C++编程魔法师c++机器学习开发语言
随着深度学习模型逐渐从研究走向生产环境,推理能力成为部署中的关键环节。模型的推理引擎需要以极低的延迟快速处理输入数据,同时最大化地利用硬件资源。虽然Python被广泛用于模型的训练和开发,但C++却在推理领域独占鳌头,其性能优势和硬件控制能力无可替代。在这篇文章中,我们将从为什么选择C++、构建高效推理引擎的细节,以及相似的开源项目三个方面深入探讨如何利用C++打造高效的机器学习推理引擎。目录为什
- 从简单到深刻的认知发展
AI架构设计之禅
计算机软件编程原理与应用实践javapythonjavascriptkotlingolang架构人工智能
认知发展,人工智能,深度学习,神经网络,机器学习,自然语言处理,计算机视觉1.背景介绍认知发展是人类从简单到复杂的思维方式演进的过程,它涉及感知、记忆、语言、推理和决策等多个方面。随着人工智能技术的飞速发展,我们开始尝试用计算机模拟人类的认知能力,构建能够学习、理解和解决复杂问题的智能系统。从早期的符号逻辑到如今的深度学习,人工智能的发展经历了多个阶段。早期的人工智能研究主要集中在规则和逻辑推理上
- 大数据和智能数据应用架构系列教程之:大数据与人工智能
AI天才研究院
AI实战大数据AI人工智能Python实战大数据人工智能语言模型JavaPython架构设计
作者:禅与计算机程序设计艺术1.背景介绍概述“大数据”是指海量、高维、多样化的数据集合。随着人类对数据处理和管理的需求越来越复杂,越来越依赖机器学习、人工智能等新兴技术。在过去的一段时间里,越来越多的人开始关注到“大数据”这一颗龙头。如今,“大数据”已经成为一个新的名词,它既包含了大量的数据,也带来了巨大的价值。因此,研究、开发、应用“大数据”技术也逐渐成为各行各业的专业人才需求。在这个快速发展的
- 【前沿聚焦】机器学习的未来版图:从自动化到隐私保护的技术突破
网罗开发
人工智能AI大模型机器学习人工智能
网罗开发(小红书、快手、视频号同名) 大家好,我是展菲,目前在上市企业从事人工智能项目研发管理工作,平时热衷于分享各种编程领域的软硬技能知识以及前沿技术,包括iOS、前端、HarmonyOS、Java、Python等方向。在移动端开发、鸿蒙开发、物联网、嵌入式、云原生、开源等领域有深厚造诣。图书作者:《ESP32-C3物联网工程开发实战》图书作者:《SwiftUI入门,进阶与实战》超级个体:CO
- 机器学习&深度学习目录
UQI-LIUWJ
各专栏目录深度学习人工智能1024程序员节
机器学习模型机器学习笔记:Transformer_刘文巾的博客-CSDN博客attention相关机器学习笔记:attention_UQI-LIUWJ的博客-CSDN博客机器学习笔记:ELMOBERT_UQI-LIUWJ的博客-CSDN博客机器学习笔记:ViT(论文AnImageIsWorth16X16Words:TransformersforImageRecognitionatScale)_UQ
- 06-机器学习-数据预处理
不会打代码呜呜呜呜
机器学习机器学习人工智能
数据清洗数据清洗是数据预处理的核心步骤,旨在修正或移除数据集中的错误、不完整、重复或不一致的部分,为后续分析和建模提供可靠基础。以下是数据清洗的详细流程、方法和实战示例:一、数据清洗的核心任务问题类型表现示例影响缺失值数值型字段为空(NaN)模型无法处理缺失值,导致训练中断或偏差异常值年龄=200岁,房价=-100万扭曲统计指标(如均值),降低模型泛化性重复数据两行记录完全相同导致模型过拟合,降低
- 从零推导线性回归:最小二乘法与梯度下降的数学原理
Echo-Nie
机器学习机器学习线性回归人工智能梯度下降数学推导
欢迎来到我的主页:【Echo-Nie】本篇文章收录于专栏【机器学习】本文所有内容相关代码都可在以下仓库中找到:Github-MachineLearning1线性回归1.1什么是线性回归线性回归是一种用来预测和分析数据之间关系的工具。它的核心思想是找到一条直线(或者一个平面),让这条直线尽可能地“拟合”已有的数据点,通过这条直线,我们可以预测新的数据。eg:假设你想预测房价,你知道房子的大小(面积)
- 超实用的 30 段 Python 案例(上)
Python之栈
python开发语言
Python是目前最流行的语言之一,它在数据科学、机器学习、web开发、脚本编写、自动化方面被许多人广泛使用。它的简单和易用性造就了它如此流行的原因。如果你正在阅读本文,那么你或多或少已经使用过Python或者对Python感兴趣。在本文中,我们将会介绍30个简短的代码片段,你可以在30秒或更短的时间里理解和学习这些代码片段。1.检查重复元素下面的方法可以检查给定列表中是否有重复的元素。它使用了s
- cv python_python里面cv是什么意思
weixin_40004659
cvpython
OpenCV(OpenSourceComputerVisionLibrary)开放源代码计算机视觉库,主要算法涉及图像处理、计算机视觉和机器学习相关方法。OpenCV其实就是一堆C和C++语言的源代码文件,这些源代码文件中实现了许多常用的计算机视觉算法。OpenCV由一系列C函数和C++类构成,它有C,C++,Python和java接口,当前SDK(SoftwareDevelopmentKit软件
- #深度学习:从基础到实践
single_ffish
深度学习gpt神经网络生成对抗网络1024程序员节
深度学习是人工智能领域近年来最为火热的技术之一。它通过构建由多个隐藏层组成的神经网络模型,能够从海量数据中自动学习特征和表征,在图像识别、自然语言处理、语音识别等领域取得了突破性进展。本文将全面介绍深度学习的基础知识、主要算法和实践应用,帮助您快速掌握这一前沿技术。1.深度学习的基础1.1人工神经网络深度学习是基于人工神经网络(ArtificialNeuralNetwork,ANN)的一种机器学习
- 机器学习入门——机器学习基本概念
四月是你的
机器学习
@机器学习什么是机器学习机器学习(MachineLearning,ML)是一门多领域交叉学科,涉及概率论、统计学、逼近论、凸分析、算法复杂度理论等多门学科。专门研究计算机怎样模拟或实现人类的学习行为,以获取新的知识或技能,重新组织已有的知识结构使之不断改善自身的性能。它是人工智能的核心,是使计算机具有智能的根本途径,其应用遍及人工智能的各个领域,它主要使用归纳、综合而不是演绎简单来说机器学习就是机
- python 基本知识
达达玲玲
python开发语言
Python:背景知识及环境安装什么是Python?Python是一种解释型、面向对象的高级编程语言。它的设计哲学强调代码的可读性和简洁性,因此被广泛应用于各种领域,包括:数据科学与机器学习:NumPy,Pandas,Matplotlib,Scikit-learn等库让Python成为了数据分析和机器学习的首选语言。Web开发:Django,Flask等框架提供了高效的Web开发解决方案。自动化:
- 【Python】已解决:error: subprocess-exited-with-error
屿小夏
python开发语言linux
个人简介:某不知名博主,致力于全栈领域的优质博客分享|用最优质的内容带来最舒适的阅读体验!文末获取免费IT学习资料!文末获取更多信息精彩专栏推荐订阅收藏专栏系列直达链接相关介绍书籍分享点我跳转书籍作为获取知识的重要途径,对于IT从业者来说更是不可或缺的资源。不定期更新IT图书,并在评论区抽取随机粉丝,书籍免费包邮到家AI前沿点我跳转探讨人工智能技术领域的最新发展和创新,涵盖机器学习、深度学习、自然
- chatgpt赋能python:Python如何删除一个对象
atest166
ChatGptchatgptjvmjava计算机
Python如何删除一个对象Python是一种高级、面向对象、动态类型解释型语言,它有广泛的应用,尤其在数据分析、机器学习、人工智能和Web开发等领域。但是,在Python编程过程中,我们也可能需要删除对象。那么,Python如何删除一个对象呢?Python对象和变量在Python中,一切都是对象。对象是内存中的一块数据,有自己的身份、类型和值。变量是指向对象的引用,通过变量可以访问对象的属性和方
- AI在电商平台商品描述生成中的应用
AI天才研究院
计算AI大模型企业级应用开发实战大数据AI人工智能javapythonjavascriptkotlingolang架构人工智能大厂程序员硅基计算碳基计算认知计算生物计算深度学习神经网络大数据AIGCAGILLM系统架构设计软件哲学Agent程序员实现财富自由
AI在电商平台商品描述生成中的应用关键词:人工智能、电商平台、商品描述、自然语言处理、机器学习、深度学习摘要:本文深入探讨了人工智能在电商平台商品描述生成中的应用。首先,我们回顾了人工智能的概述和电商平台的发展背景。随后,分析了商品描述在电商平台中的重要性以及存在的问题。接下来,我们重点介绍了AI在商品描述生成中的应用技术,包括自然语言处理、机器学习和深度学习等。文章还通过实战案例展示了AI商品描
- 使用 PyTorch 实现逻辑回归:从数据到模型保存与加载
弥树子
pytorch逻辑回归人工智能
在机器学习中,逻辑回归是一种经典的分类算法,广泛应用于二分类问题。本文将通过一个简单的示例,展示如何使用PyTorch框架实现逻辑回归模型,从数据准备到模型训练、保存和加载,最后进行预测。1.数据准备逻辑回归的核心是通过学习数据中的特征与标签之间的关系来进行分类。在本示例中,我们手动创建了一个简单的二维数据集,包含两类数据点。第一类数据点的标签为0,第二类数据点的标签为1。class1_point
- 【Python】已解决:(cmd进入Python环境报错)No Python at ‘C:\Users…\Python\Python39\python.exe’
屿小夏
pythonlinux开发语言
个人简介:某不知名博主,致力于全栈领域的优质博客分享|用最优质的内容带来最舒适的阅读体验!文末获取免费IT学习资料!文末获取更多信息精彩专栏推荐订阅收藏专栏系列直达链接相关介绍书籍分享点我跳转书籍作为获取知识的重要途径,对于IT从业者来说更是不可或缺的资源。不定期更新IT图书,并在评论区抽取随机粉丝,书籍免费包邮到家AI前沿点我跳转探讨人工智能技术领域的最新发展和创新,涵盖机器学习、深度学习、自然
- 【机器学习】 自定义数据集 使用tensorflow框架实现逻辑回归并保存模型,然后保存模型后再加载模型进行预测
加德霍克
tensorflow逻辑回归人工智能python作业
一、使用tensorflow框架实现逻辑回归1.数据部分:首先自定义了一个简单的数据集,特征X是100个随机样本,每个样本一个特征,目标值y基于线性关系并添加了噪声。tensorflow框架不需要numpy数组转换为相应的张量,可以直接在模型中使用数据集。2.模型定义部分:方案1:model=tf.keras.Sequential([tf.keras.layers.Dense(1,input_sh
- [黑洞与暗粒子]没有光的世界
comsci
无论是相对论还是其它现代物理学,都显然有个缺陷,那就是必须有光才能够计算
但是,我相信,在我们的世界和宇宙平面中,肯定存在没有光的世界....
那么,在没有光的世界,光子和其它粒子的规律无法被应用和考察,那么以光速为核心的
&nbs
- jQuery Lazy Load 图片延迟加载
aijuans
jquery
基于 jQuery 的图片延迟加载插件,在用户滚动页面到图片之后才进行加载。
对于有较多的图片的网页,使用图片延迟加载,能有效的提高页面加载速度。
版本:
jQuery v1.4.4+
jQuery Lazy Load v1.7.2
注意事项:
需要真正实现图片延迟加载,必须将真实图片地址写在 data-original 属性中。若 src
- 使用Jodd的优点
Kai_Ge
jodd
1. 简化和统一 controller ,抛弃 extends SimpleFormController ,统一使用 implements Controller 的方式。
2. 简化 JSP 页面的 bind, 不需要一个字段一个字段的绑定。
3. 对 bean 没有任何要求,可以使用任意的 bean 做为 formBean。
使用方法简介
- jpa Query转hibernate Query
120153216
Hibernate
public List<Map> getMapList(String hql,
Map map) {
org.hibernate.Query jpaQuery = entityManager.createQuery(hql);
if (null != map) {
for (String parameter : map.keySet()) {
jp
- Django_Python3添加MySQL/MariaDB支持
2002wmj
mariaDB
现状
首先,
[email protected] 中默认的引擎为 django.db.backends.mysql 。但是在Python3中如果这样写的话,会发现 django.db.backends.mysql 依赖 MySQLdb[5] ,而 MySQLdb 又不兼容 Python3 于是要找一种新的方式来继续使用MySQL。 MySQL官方的方案
首先据MySQL文档[3]说,自从MySQL
- 在SQLSERVER中查找消耗IO最多的SQL
357029540
SQL Server
返回做IO数目最多的50条语句以及它们的执行计划。
select top 50
(total_logical_reads/execution_count) as avg_logical_reads,
(total_logical_writes/execution_count) as avg_logical_writes,
(tot
- spring UnChecked 异常 官方定义!
7454103
spring
如果你接触过spring的 事物管理!那么你必须明白 spring的 非捕获异常! 即 unchecked 异常! 因为 spring 默认这类异常事物自动回滚!!
public static boolean isCheckedException(Throwable ex)
{
return !(ex instanceof RuntimeExcep
- mongoDB 入门指南、示例
adminjun
javamongodb操作
一、准备工作
1、 下载mongoDB
下载地址:http://www.mongodb.org/downloads
选择合适你的版本
相关文档:http://www.mongodb.org/display/DOCS/Tutorial
2、 安装mongoDB
A、 不解压模式:
将下载下来的mongoDB-xxx.zip打开,找到bin目录,运行mongod.exe就可以启动服务,默
- CUDA 5 Release Candidate Now Available
aijuans
CUDA
The CUDA 5 Release Candidate is now available at http://developer.nvidia.com/<wbr></wbr>cuda/cuda-pre-production. Now applicable to a broader set of algorithms, CUDA 5 has advanced fe
- Essential Studio for WinRT网格控件测评
Axiba
JavaScripthtml5
Essential Studio for WinRT界面控件包含了商业平板应用程序开发中所需的所有控件,如市场上运行速度最快的grid 和chart、地图、RDL报表查看器、丰富的文本查看器及图表等等。同时,该控件还包含了一组独特的库,用于从WinRT应用程序中生成Excel、Word以及PDF格式的文件。此文将对其另外一个强大的控件——网格控件进行专门的测评详述。
网格控件功能
1、
- java 获取windows系统安装的证书或证书链
bewithme
windows
有时需要获取windows系统安装的证书或证书链,比如说你要通过证书来创建java的密钥库 。
有关证书链的解释可以查看此处 。
public static void main(String[] args) {
SunMSCAPI providerMSCAPI = new SunMSCAPI();
S
- NoSQL数据库之Redis数据库管理(set类型和zset类型)
bijian1013
redis数据库NoSQL
4.sets类型
Set是集合,它是string类型的无序集合。set是通过hash table实现的,添加、删除和查找的复杂度都是O(1)。对集合我们可以取并集、交集、差集。通过这些操作我们可以实现sns中的好友推荐和blog的tag功能。
sadd:向名称为key的set中添加元
- 异常捕获何时用Exception,何时用Throwable
bingyingao
用Exception的情况
try {
//可能发生空指针、数组溢出等异常
} catch (Exception e) {
- 【Kafka四】Kakfa伪分布式安装
bit1129
kafka
在http://bit1129.iteye.com/blog/2174791一文中,实现了单Kafka服务器的安装,在Kafka中,每个Kafka服务器称为一个broker。本文简单介绍下,在单机环境下Kafka的伪分布式安装和测试验证 1. 安装步骤
Kafka伪分布式安装的思路跟Zookeeper的伪分布式安装思路完全一样,不过比Zookeeper稍微简单些(不
- Project Euler
bookjovi
haskell
Project Euler是个数学问题求解网站,网站设计的很有意思,有很多problem,在未提交正确答案前不能查看problem的overview,也不能查看关于problem的discussion thread,只能看到现在problem已经被多少人解决了,人数越多往往代表问题越容易。
看看problem 1吧:
Add all the natural num
- Java-Collections Framework学习与总结-ArrayDeque
BrokenDreams
Collections
表、栈和队列是三种基本的数据结构,前面总结的ArrayList和LinkedList可以作为任意一种数据结构来使用,当然由于实现方式的不同,操作的效率也会不同。
这篇要看一下java.util.ArrayDeque。从命名上看
- 读《研磨设计模式》-代码笔记-装饰模式-Decorator
bylijinnan
java设计模式
声明: 本文只为方便我个人查阅和理解,详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/
import java.io.BufferedOutputStream;
import java.io.DataOutputStream;
import java.io.FileOutputStream;
import java.io.Fi
- Maven学习(一)
chenyu19891124
Maven私服
学习一门技术和工具总得花费一段时间,5月底6月初自己学习了一些工具,maven+Hudson+nexus的搭建,对于maven以前只是听说,顺便再自己的电脑上搭建了一个maven环境,但是完全不了解maven这一强大的构建工具,还有ant也是一个构建工具,但ant就没有maven那么的简单方便,其实简单点说maven是一个运用命令行就能完成构建,测试,打包,发布一系列功
- [原创]JWFD工作流引擎设计----节点匹配搜索算法(用于初步解决条件异步汇聚问题) 补充
comsci
算法工作PHP搜索引擎嵌入式
本文主要介绍在JWFD工作流引擎设计中遇到的一个实际问题的解决方案,请参考我的博文"带条件选择的并行汇聚路由问题"中图例A2描述的情况(http://comsci.iteye.com/blog/339756),我现在把我对图例A2的一个解决方案公布出来,请大家多指点
节点匹配搜索算法(用于解决标准对称流程图条件汇聚点运行控制参数的算法)
需要解决的问题:已知分支
- Linux中用shell获取昨天、明天或多天前的日期
daizj
linuxshell上几年昨天获取上几个月
在Linux中可以通过date命令获取昨天、明天、上个月、下个月、上一年和下一年
# 获取昨天
date -d 'yesterday' # 或 date -d 'last day'
# 获取明天
date -d 'tomorrow' # 或 date -d 'next day'
# 获取上个月
date -d 'last month'
#
- 我所理解的云计算
dongwei_6688
云计算
在刚开始接触到一个概念时,人们往往都会去探寻这个概念的含义,以达到对其有一个感性的认知,在Wikipedia上关于“云计算”是这么定义的,它说:
Cloud computing is a phrase used to describe a variety of computing co
- YII CMenu配置
dcj3sjt126com
yii
Adding id and class names to CMenu
We use the id and htmlOptions to accomplish this. Watch.
//in your view
$this->widget('zii.widgets.CMenu', array(
'id'=>'myMenu',
'items'=>$this-&g
- 设计模式之静态代理与动态代理
come_for_dream
设计模式
静态代理与动态代理
代理模式是java开发中用到的相对比较多的设计模式,其中的思想就是主业务和相关业务分离。所谓的代理设计就是指由一个代理主题来操作真实主题,真实主题执行具体的业务操作,而代理主题负责其他相关业务的处理。比如我们在进行删除操作的时候需要检验一下用户是否登陆,我们可以删除看成主业务,而把检验用户是否登陆看成其相关业务
- 【转】理解Javascript 系列
gcc2ge
JavaScript
理解Javascript_13_执行模型详解
摘要: 在《理解Javascript_12_执行模型浅析》一文中,我们初步的了解了执行上下文与作用域的概念,那么这一篇将深入分析执行上下文的构建过程,了解执行上下文、函数对象、作用域三者之间的关系。函数执行环境简单的代码:当调用say方法时,第一步是创建其执行环境,在创建执行环境的过程中,会按照定义的先后顺序完成一系列操作:1.首先会创建一个
- Subsets II
hcx2013
set
Given a collection of integers that might contain duplicates, nums, return all possible subsets.
Note:
Elements in a subset must be in non-descending order.
The solution set must not conta
- Spring4.1新特性——Spring缓存框架增强
jinnianshilongnian
spring4
目录
Spring4.1新特性——综述
Spring4.1新特性——Spring核心部分及其他
Spring4.1新特性——Spring缓存框架增强
Spring4.1新特性——异步调用和事件机制的异常处理
Spring4.1新特性——数据库集成测试脚本初始化
Spring4.1新特性——Spring MVC增强
Spring4.1新特性——页面自动化测试框架Spring MVC T
- shell嵌套expect执行命令
liyonghui160com
一直都想把expect的操作写到bash脚本里,这样就不用我再写两个脚本来执行了,搞了一下午终于有点小成就,给大家看看吧.
系统:centos 5.x
1.先安装expect
yum -y install expect
2.脚本内容:
cat auto_svn.sh
#!/bin/bash
- Linux实用命令整理
pda158
linux
0. 基本命令 linux 基本命令整理
1. 压缩 解压 tar -zcvf a.tar.gz a #把a压缩成a.tar.gz tar -zxvf a.tar.gz #把a.tar.gz解压成a
2. vim小结 2.1 vim替换 :m,ns/word_1/word_2/gc
- 独立开发人员通向成功的29个小贴士
shoothao
独立开发
概述:本文收集了关于独立开发人员通向成功需要注意的一些东西,对于具体的每个贴士的注解有兴趣的朋友可以查看下面标注的原文地址。
明白你从事独立开发的原因和目的。
保持坚持制定计划的好习惯。
万事开头难,第一份订单是关键。
培养多元化业务技能。
提供卓越的服务和品质。
谨小慎微。
营销是必备技能。
学会组织,有条理的工作才是最有效率的。
“独立
- JAVA中堆栈和内存分配原理
uule
java
1、栈、堆
1.寄存器:最快的存储区, 由编译器根据需求进行分配,我们在程序中无法控制.2. 栈:存放基本类型的变量数据和对象的引用,但对象本身不存放在栈中,而是存放在堆(new 出来的对象)或者常量池中(字符串常量对象存放在常量池中。)3. 堆:存放所有new出来的对象。4. 静态域:存放静态成员(static定义的)5. 常量池:存放字符串常量和基本类型常量(public static f