可视化的用Python学习线性回归，闭式求解法(closed form)

本文用Numpy生成测试数据，并且用线性回归来求解预测函数。通过Matplotlib来可视化数据和代价函数，这样我们可以对代价函数有更直观的理解。

也叫Normal Function

import numpy as np
import math
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

"""Prepare Data"""
 
x = 5+ 5*np.random.randn(100)
y = 3*x + 4 + 3*np.random.randn(100)

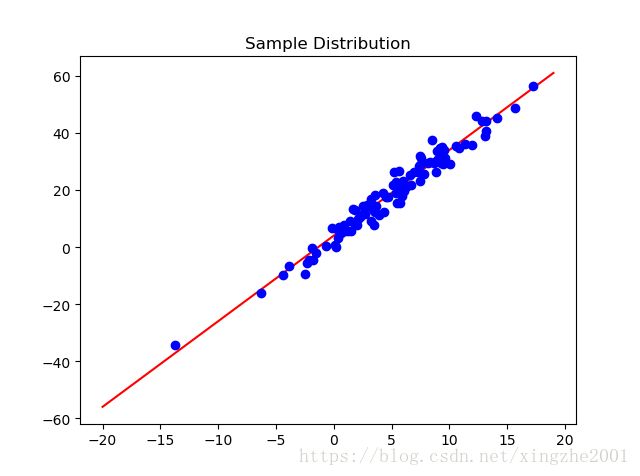
'''Show the data'''
plt.title("Sample Distribution")
plt.plot(np.arange(-20,20), 3*np.arange(-20,20)+4, "r")
plt.plot(x,y,"bo")

plt.show()

"""Show Cost Function"""
wa=np.arange(-7,14)
cost=np.zeros(21)


for i in range(-7,18):
	cost[i]=((wa[i]*x+4-y)**2).sum()/len(x)

plt.title("Cost Function for LSM for w only")
plt.plot(wa, cost)
plt.show()

wix = np.arange(-7,13,0.1);
wiy = np.arange(-6,14,0.1);

Wi,Bi = np.meshgrid(wix,wiy)

cost2d = np.zeros([200,200])

for i in range(len(Wi)):
	for j in range(len(Bi)):		
		cost2d[i][j]=((wix[j]*x+wiy[i]-y)**2).sum()/len(x)


fig = plt.figure()
plt3d=Axes3D(fig)

plt.title("The 3D view of cost function Cost(w,b)")
plt3d.set_xlabel("Wi")
plt3d.set_ylabel("Bi")
plt3d.set_zlabel("Cost")
plt3d.plot_surface(Wi, Bi, cost2d, cmap=plt.cm.winter)
plt.show()


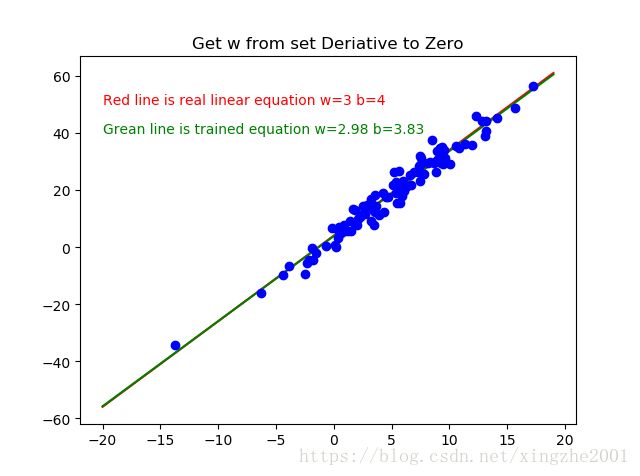
'''Get the minimal cost function'''
'''Set d_cost/dw = 0 we got'''
sum_xy = (x*y).sum()
sum_x = x.sum()
sum_xx = (x**2).sum()
wi=(sum_xy - 4*sum_x)/sum_xx

'''set d_cost/db = 0 we got'''
sum_y = y.sum()
bi = (sum_y - wi*sum_x)/len(x)

plt.title("Get w from set Deriative to Zero")
plt.text(-20, 50, "Red line is real linear equation w={0} b={1}".format(3,4), color="red")
plt.text(-20, 40, "Grean line is trained equation w={0:.2f} b={1:.2f}".format(wi,bi), color="green")
plt.plot(np.arange(-20,20), 3*np.arange(-20,20)+4, "r")
plt.plot(np.arange(-20,20), wi*np.arange(-20,20)+bi, "g")
plt.plot(x,y,"bo")
plt.show()

生成的图有