vivo2020届春季校园招聘在线编程考试 解题报告 Apare_xzc

vivo2020届春季校园招聘在线编程考试 解题报告

---

题目链接：牛客链接

---

A. 手机屏幕解锁模式

分析：

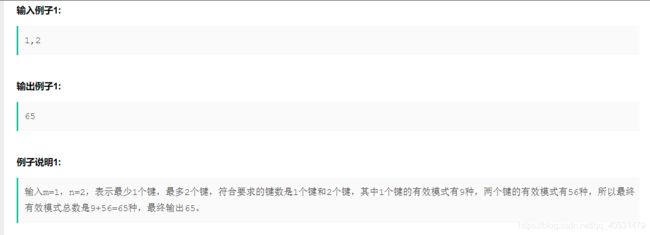
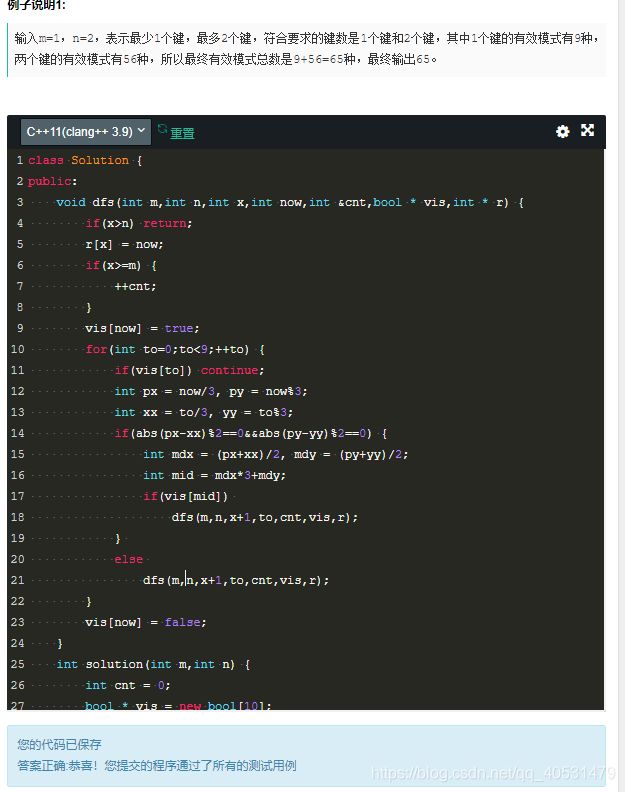
        这是一个智能手机的图案锁，有3*3=9个点。现在要求所有图案中经过的点的个数再[m,n]这个范围内的方案数。一个点也算作一种方案(和一般图案锁不太一样)。
        我们可以大致计算一下总共方案的个数，大概是9！这么多。当然，我们只是算了个大概，没有考虑图案的限制。这个大小远远小于10^8, 我们可以直接dfs所有方案。我们从9个点都出发一遍，每次在1-9之中都判断一次，如果还没走过，就可以考虑走到这个点。 我们一路dfs下去，如果遇到一个方案它的路径长度(经过点的个数)在[m,n]范围之内，我们就计数。如果路径长度大于n, 我们就不必往下继续搜索了。
        我们需要注意一个问题，就是如果路径之中的前后两个点A, C中间那个点B还没有走过，我们就不能跨过这个点，不然A->B->C会被重复计数，因为dfs(A)的时候已经去过B了。
        这题要求写在测试类里面，int solution(int m,int n)

代码：

#include 
using namespace std;
void dfs(int m,int n,int x,int now,int &cnt,bool * vis,int * r) {
	if(x>n) return;
	r[x] = now;
	if(x>=m) {
		++cnt;
//		for(int i=1;i<=x;++i) cout<
	}
	vis[now] = true;
	for(int to=0;to<9;++to) {
		if(vis[to]) continue;
		int px = now/3, py = now%3;
		int xx = to/3, yy = to%3;
		if(abs(px-xx)%2==0&&abs(py-yy)%2==0) {
			int mdx = (px+xx)/2, mdy = (py+yy)/2;
			int mid = mdx*3+mdy;
			if(vis[mid]) 
				dfs(m,n,x+1,to,cnt,vis,r);
		} 
		else 
			dfs(m,n,x+1,to,cnt,vis,r);
	}
	vis[now] = false;
}
int solution(int m,int n) {
	int cnt = 0;
	bool * vis = new bool[10];
	int * r = new int[10];
	for(int i=0;i<10;++i) vis[i] = false,r[i]=-1;
	for(int i=0;i<9;++i)
		dfs(m,n,1,i,cnt,vis,r);
	delete []vis;
	delete []r;
	return cnt;
}
int main(void) {
	int m,n;
	while(cin>>m>>n) {
		cout<<solution(m,n)<<endl;
	} 
	
	return 0;
} 

直接把dfs()和solution(int m,int n)两个函数复制到class Solution()作为成员函数即可。

---

B. 数位之积

分析：

         测试类要求的函数输入的参数n和输出的答案都是int。
        我们可以分析一下, 要求y的各个数位乘积等于n。我们把n分解质因数，得到n = P1^C1 * P2^C2 * P3^C3 * ... * Pk^Ck。 因为十进制整数每个数位最大为9，所以如果n存在大于9的质因数，我们便无法实现。所以，n只能包含2,3,5,7这4个质因数。
        如果n==0,则y最小为10，如果1<=n<=9, 那么y最小为n+10,因为题目要求y>9。
        处理完特殊的小数字后我们就可以开始讨论一般的输入。

• 如果n的质因数存在大于7的，那么n不可以被y的数位乘积表示，输出-1
• n最多只含有上述的4个质因数，那么我们就可以把n表示为：n = 2^C2 * 3^C3 * 5^C5 * 7^C7。(C2,C3,C5,C7>=0)
• 我们贪心地考虑，要使得y最小，首先要使y有最少的数位，其次在最少数位的基础上，我们要使得y的字典序最小。
• 首先，5和7必须一个占一位，不然会超过9。我们先把2^3替换为8，3^2替换为9，这样能有效减少数位。然后3可能剩下0或1个，2可能剩下0,1,2个。如果只剩下2，优先把2^2都替换为4。如果有1个3，1个2，就替换为6。如果有2个2一个3，就替换为2，6。
• 我们处理出2，3，4，5，6，7，8，9的个数后，就可以贪心地小数在前大数在后得到答案了。

代码：

#include 
using namespace std;
int solution(int n) {
	if(n==0) return 10;
	if(n<=9) return 10+n;
	int c2 = 0, c3 = 0, c5 = 0, c7 = 0;
	while(n%2==0) c2++, n/=2;
	while(n%3==0) c3++, n/=3;
	while(n%5==0) c5++, n/=5;
	while(n%7==0) c7++, n/=7;
	if(n>1) return -1;  
	int c8 = 0, c9=0,c4=0,c6=0;
	c8 = c2/3; c2 %= 3;
	c9 = c3/2; c3 %= 2;
	if(c3==0) {
		c4 = c2/2; c2%=2;
	} else { //c3==1
		if(c2==1) c2=0,c3=0,c6=1;
		else if(c2==2) c2=1,c3=0,c6=1;
	}
	int ans = 0;
	while(c2--) ans = ans*10+2;
	while(c3--) ans = ans*10+3;
	while(c4--) ans = ans*10+4;
	while(c5--) ans = ans*10+5;
	while(c6--) ans = ans*10+6;
	while(c7--) ans = ans*10+7;
	while(c8--) ans = ans*10+8;
	while(c9--) ans = ans*10+9;
	if(ans<0) return -1;
	return ans;	
} 
int main(void) {
	int x;
	while(cin>>x) {
		cout<<solution(x)<<"\n";
	}
	
	return 0;
} 

---

C. vivo智能手机产能

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 256M，其他语言512M

在vivo产线上，每位职工随着对手机加工流程认识的熟悉和经验的增加，日产量也会不断攀升。
假设第一天量产1台，接下来2天(即第二、三天)每天量产2件，接下来3天(即第四、五、六天)每天量产3件 … …
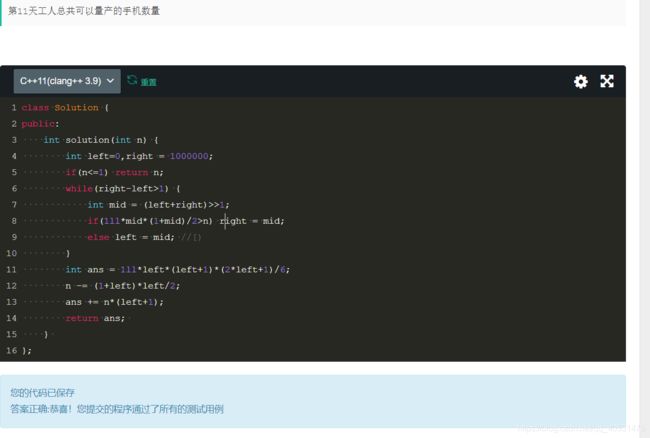
以此类推，请编程计算出第n天总共可以量产的手机数量。

分析：

        1 2 2 3 3 3 4 4 4 4 5 5 5 5 5 6 6 6 6 6 6 7 7…
        二分找出最后一个连续的数字，然后求和即可。
        1^2 + 2^2 + 3^2 + ...+n^2 = n*(n+1)*(2n+1)/6

代码：

#include 
using namespace std;
int solve(int n) {
	int left=0,right = 1000000;
	if(n<=1) return n;
	while(right-left>1) {
		int mid = (left+right)>>1;
		if(1ll*mid*(1+mid)/2>n) right = mid;
		else left = mid; //[)
	}
	int ans = 1ll*left*(left+1)*(2*left+1)/6;
	n -= (1+left)*left/2;
	ans += n*(left+1);
	return ans; 
} 
int main(void) {
	int x;
	while(cin>>x)
	{
		cout<<solve(x)<<"\n";
	}
	return 0;
} 

---

2020/4/10 12:33
xzc

---