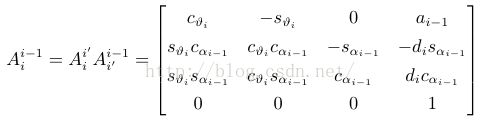機器人學總結(2) —— (正)運動學
0 前言
前面我們對機器人的描述做了說明,本節介紹運動學。運動學是通過關節參數求解末端的笛卡爾參數的過程。這裡說的運動學一般也叫正運動學,因為他的逆過程叫逆運動學(通過笛卡爾參數求解關節參數。)
機械臂是由一系列剛體(連桿)通過運動副(關節)鏈接起來的。關節從本質上可以分為兩類:轉動型和平動性。整個結構形成一個運動鏈。其中一段固定在基座上,另端鏈接穆端的執行器(工具)使得機械臂可以操作空間中的對象。機械臂的機械機構自由度唯一決定其姿態。
從拓撲學觀點出發,如果運動鏈的兩端只由一些列鏈接相連接,則運動鏈為開的;如果一些列的連桿形成了閉合的環,則機械臂包含一個閉運動鏈。
運動學的求解方法有很多種,最直接的辦法就是利用幾何關係求解,不過這種方法在機械結構比較複雜的情況下不太容易計算。一般使用其次矩陣乘法求解(請參考上一篇文章:機器人的描述),這樣計算可以用迭代算法實現,每次只是在計算矩陣乘法。不過即使是這樣我們在坐標系建立(方向)以及在參數選擇上也有很多種方法,下面介紹機器人領域比較通用的一種規範(建系和參數定義)——DH法。
1 標準DH法(standard)
Denavit和Hartenberg于1995年提出了一种为关节链中的每一杆件建立坐标系的矩阵方法,即D-H参数法。
1.1 關節參數
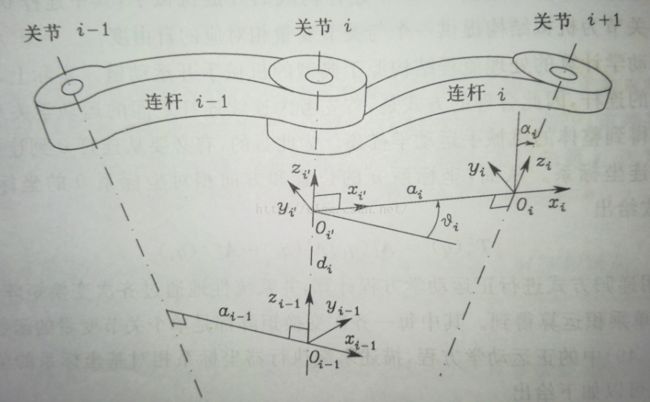
建立坐標系的過程如下:
● 沿關節 i 方向選定軸 zi-1;
● 原點 Oi 定位於軸 zi 和軸 zi-1的公垂涎的交點;同樣地 O'i 定位于公垂線與軸 zi-1 的交點;
● 沿軸 zi-1和軸 zi的公垂線選擇軸 xi,方向由關節 i 指向關節 i+1;
● 選擇軸yi 以構成右手系;
以上方法存在一些並不唯一的關節坐標系:
● 對坐標系{0},只有軸 zi的方向是制定的,因此 O0 和 x0 可以任意選擇;
● 對坐標系{n},由於沒有關節 n+1,軸 zn並不唯一,可以取和軸 zn-1相同;
● 當兩相繼軸平行時,公垂線不唯一;
● 當兩相繼軸相交時,軸 xi 的方向任意;
● 當關節 i 為移動關節時,軸 zi-1 的方向任意;
對應的參數選取如下:
ai:Oi 和 O’i 之間的距離;(公垂線長度)
di:O’i 沿 zi-1 的坐標;
αi:軸 zi-1 和軸 zi 之間的夾角,當繞軸 xi 逆時針轉動時取正;
θi:軸 xi-1 和軸 xi 之間的夾角,當繞軸 zi-1 逆時針轉動時取正;
其中有兩個參數始終為常數,只取決於官借鑒的集合鏈接,剩下兩個鐘有一個是變量取決於關節類型:
● 如果關節 i 是轉動關節,則變量為 θi;
● 如果關節 i 是平動關節,則變量為 di;
1.2 DH矩陣
可以通過以下步驟將坐標系 i 和坐標系 i-1 之間的坐標變換表示出來:
● 選取一個坐標系與{i-1}坐標系重合;
● 將這個坐標系沿軸zi-1 平移 di,并繞軸zi-1 旋轉θi;變換后得到坐標系{i’},用其次矩陣描述如下:
● 將坐標系{i’}沿軸x’i 平移 ai,并繞軸x’i 旋轉αi;變換后得到坐標系{i},用其次矩陣描述如下:
● 將上面的結果相乘得到變換矩陣:
通過上面的DH矩陣,通過迭代算法,可以依次計算出從關節1到關節n的其次矩陣。
1.3 舉例
下面我們具體舉個例子運動上面的DH法。
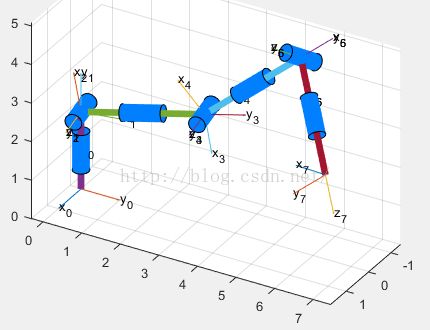
對應上面的DLR機械臂的簡圖及DH法建系如下:
得到如下DH參數表:
————————————————————————————
連桿 ai αi di θi
————————————————————————————
1 0 π/2 d1 θ1
2 0 π/2 0 θ2
3 0 π/2 d3 θ3
4 0 π/2 0 θ4
5 0 π/2 d5 θ5
6 0 π/2 0 θ6
7 0 0 d7 θ7
————————————————————————————
編寫MATLAB代碼繪製圖形(為了繪圖清晰,這裡把坐標系{0}向下移動了一下)
MATLAB代碼如下(其中調用的函數在本文下面的附錄中給出):
%% 參數定義
joint_size = 7+1; % 關節數
a = [0, 0, 0, 0, 0, 0, 0]; % DH參數
alpha = [90, 90, 90, 90, 90, 90, 0]; % 角度(非弧度)
d = [2, 0, 3, 0 ,3, 0, 3]; % d取數值,為了作圖
cta = [100, 100, 180, -150, 135, 90, 90]; % 角度(非弧度)
% 定義數組存儲其次矩陣、姿態矩陣、位置向量
T = cell(joint_size);
R = cell(joint_size);
P = cell(joint_size);
% 基座標系定義
T{1} = [1 0 0 0; 0 1 0 0; 0 0 1 0; 0 0 0 1];
P{1} = T{1}(1:3, 4);
R{1} = T{1}(1:3, 1:3);
% (迭代)循環計算每個關節的其次矩陣
for k=2:joint_size
T{k} = T{k-1}*DH(a(k-1), radians(alpha(k-1)), d(k-1), radians(cta(k-1)));
P{k} = T{k}(1:3, 4);
R{k} = T{k}(1:3, 1:3);
end
% 繪圖
clf;
DrawCoordinate('1', P{1}, R{1});
for k=2:joint_size
DrawLine(P{k-1}, P{k});
DrawCylinder((P{k-1}+P{k})/2, R{k-1});
DrawCoordinate('0'+k-1, P{k}, R{k});
end
% 顯示參數
axis equal; % 顯示坐標軸比例
view(120,30); % 指定子图1的视点2 改良DH法(modify DH)
上面的DH法有問題 :關節下標不對應(用標準DH模型處理tree structure robot或closed loop structure robot 會產生奇異 —— Wisama Khalil)。為了解決問題存在一些不同的修正DH法(modify DH)。下面介紹其中的以一種(克雷格)。
2.1 關節參數
建立坐標系過程如下:
● 沿關節 i-1 方向選定軸 zi-1;
● 原點 Oi-1 定位於軸 zi 和軸 zi-1的公垂涎的交點;同樣地 O'i 定位于公垂線與軸 zi 的交點;
● 沿軸 zi-1和軸 zi的公垂線選擇軸 xi-1,方向由關節 i-1 指向關節 i;
● 選擇軸 yi 以構成右手系;
以上方法存在一些並不唯一的關節坐標系:
● 對坐標系{0},可以取初始和坐標系{1}相同;
● 對坐標系{n},可以取初始和坐標系 {n-1}相同;
● 當兩相繼軸平行時,公垂線不唯一;
● 當兩相繼軸相交時,軸 xi-1 的方向垂直于軸 zi-1和軸 zi 的平面;
● 當關節 i 為移動關節時,軸 zi-1 的方向任意;
對應的參數選取如下:
ai:Oi-1 和 O’i 之間的距離;(公垂線長度)
di:O’i 沿 zi 的坐標;(軸 xi-1 與軸xi 的距離)
αi:軸 zi 和軸 zi+1 之間的夾角,當繞軸 xi 逆時針轉動時取正;
θi:軸 xi-1 和軸 xi 之間的夾角,當繞軸 zi 逆時針轉動時取正;
其中有兩個參數始終為常數,只取決於官借鑒的集合鏈接,剩下兩個鐘有一個是變量取決於關節類型:
● 如果關節 i 是轉動關節,則變量為 θi;
● 如果關節 i 是平動關節,則變量為 di;
2.2 DH矩陣
可以通過以下步驟將坐標系 i 和坐標系 i-1 之間的坐標變換表示出來:
● 選取一個坐標系與{i-1}坐標系重合;
● 將這個坐標系{i-1}沿軸xi-1 平移 ai-1,并繞軸xi-1 旋轉αi-1;變換后得到坐標系{i’},用其次矩陣描述如下:
● 將坐標系沿軸zi 平移 di,并繞軸zi 旋轉θi;變換后得到坐標系{i},用其次矩陣描述如下:
● 將上面的結果相乘得到變換矩陣:
通過上面的DH矩陣,通過迭代算法,可以依次計算出從關節1到關節n的其次矩陣。
2.3 舉例
下面我們將DLR機械臂的例子,通過改良DH法求解一下。
改良DH參數表:
————————————————————————————
連桿 ai-1 αi-1 di θi
————————————————————————————
1 0 0 d1 θ1
2 0 π/2 0 θ2
3 0 π/2 d3 θ3
4 0 π/2 0 θ4
5 0 π/2 d5 θ5
6 0 π/2 0 θ6
7 0 π/2 d7 θ7
————————————————————————————
編寫MATLAB代碼繪製圖形
MATLAB代碼如下(其中調用的函數在本文下面的附錄中給出):
%% 參數定義
joint_size = 7+1; % 關節數
a = [0, 0, 0, 0, 0, 0, 0]; % DH參數
alpha = [0, 90, 90, 90, 90, 90, 90]; % 角度(非弧度)
d = [2, 0, 3, 0 ,3, 0, 3]; % d取數值,為了作圖
cta = [100, 100, 180, -150, 135, 90, 90]; % 角度(非弧度)
% 定義數組存儲其次矩陣、姿態矩陣、位置向量
T = cell(joint_size);
R = cell(joint_size);
P = cell(joint_size);
% 基座標系定義
T{1} = [1 0 0 0; 0 1 0 0; 0 0 1 0; 0 0 0 1];
P{1} = T{1}(1:3, 4);
R{1} = T{1}(1:3, 1:3);
% (迭代)循環計算每個關節的其次矩陣
for k=2:joint_size
T{k} = T{k-1}*MDH(a(k-1), radians(alpha(k-1)), d(k-1), radians(cta(k-1)));
P{k} = T{k}(1:3, 4);
R{k} = T{k}(1:3, 1:3);
end
% 繪圖
clf;
DrawCoordinate('0', P{1}, R{1});
for k=2:joint_size
DrawLine(P{k-1}, P{k});
DrawCylinder((P{k-1}+P{k})/2, R{k});
DrawCoordinate('0'+k-1, P{k}, R{k});
end
% 顯示參數
axis equal; % 顯示坐標軸比例
view(120,30); % 指定子图1的视点3 閉鏈
前面都是關於開鏈的情況,下面介紹一下 閉鏈的處理方法。
求解過程:
● 首先將鏈拆開,上圖的坐標系{j},分成多個開鏈;
● 利用DH法計算其次矩陣;
● 建立閉鏈的約束(個開鏈的末端位姿相同),減少關節變量;
● 利用規約后的關節變量求解其次變換得到正運動學方程;
4 附錄
這裡提供了matlab的作圖函數以及DH矩陣函數:
繪圖函數:
% 绘制坐标系 參數:坐標系名字name,坐標系位置p,坐標系姿態(可選參數,缺省為單位陣)
function DrawCoordinate(name, p, varargin)
% 以(x, y, z)为原点(R)为方向绘制坐标系
R = [1 0 0; 0 1 0; 0 0 1];
if numel(varargin) == 1
R = varargin{1};
end
quiver3(p(1), p(2), p(3), R(1,1), R(2,1), R(3,1), 1);
hold on;
quiver3(p(1), p(2), p(3), R(1,2), R(2,2), R(3,2), 1);
hold on;
quiver3(p(1), p(2), p(3), R(1,3), R(2,3), R(3,3), 1);
hold on;
text(p(1), p(2), p(3), '');
text(p(1)+R(1,1), p(2)+R(2,1), p(3)+R(3,1), ['x_', name]);
text(p(1)+R(1,2), p(2)+R(2,2), p(3)+R(3,2), ['y_', name]);
text(p(1)+R(1,3), p(2)+R(2,3), p(3)+R(3,3), ['z_', name]);
hold on;
end% 绘制直線 參數:起始點向量p,結束點向量q
function DrawLine(p, q)
% 以(x, y, z)为原点(R)为方向绘制坐标系
plot3([p(1) q(1)], [p(2) q(2)], [p(3) q(3)], 'LineWidth', 5);
R = [1 0 0; 0 1 0; 0 0 1];
hold on;
end% 绘制圓柱 參數:繪圖位置P,圓柱姿態矩陣R
function DrawCylinder(P, R)
r=0.2;%圆柱半径
n=50;%设置多少个边逼近圆
[x,y,z]=cylinder(r,n);%生成标准的100个面的圆柱数据,半径为r,高为1,底面圆心0,0;
z=[z(1,:)-0.5;z(2,:)-0.5];%圆柱高增高,变为高h
for k=1:n+1
xx1 = R(1,1)*x(1,k)+R(1,2)*y(1,k)+R(1,3)*z(1,k)+P(1);
yy1 = R(2,1)*x(1,k)+R(2,2)*y(1,k)+R(2,3)*z(1,k)+P(2);
zz1 = R(3,1)*x(1,k)+R(3,2)*y(1,k)+R(3,3)*z(1,k)+P(3);
xx2 = R(1,1)*x(2,k)+R(1,2)*y(2,k)+R(1,3)*z(2,k)+P(1);
yy2 = R(2,1)*x(2,k)+R(2,2)*y(2,k)+R(2,3)*z(2,k)+P(2);
zz2 = R(3,1)*x(2,k)+R(3,2)*y(2,k)+R(3,3)*z(2,k)+P(3);
x(1,k) = xx1; x(2,k) = xx2;
y(1,k) = zz1; y(2,k) = zz2;
z(1,k) = yy1; z(2,k) = yy2;
end
%为变成实心封顶添加数据
z2=[z(1,:);z;z(2,:)];
x2=[x(1,:);x;x(2,:)];
y2=[y(1,:);y;y(2,:)];
z3=[z(1,:);z(1,:)];
x3=[x(1,:);x(1,:)];
y3=[y(1,:);y(1,:)];
z4=[z(2,:);z(2,:)];
x4=[x(2,:);x(2,:)];
y4=[y(2,:);y(2,:)];
surf(x2,z2,y2,'LineStyle','none')
map=jet(16);
cl=4;%可设置16种颜色(1-16)
colormap(map(cl,:))
hold on
surf(x3,z3,y3);
hold on
surf(x4,z4,y4);
hold on
endDH矩陣函數:
%% 计算DH矩阵 參數a, alpha, d, cta
function [ans] = DH(a, alpha, d, cta)
ans = [
cos(cta) -sin(cta)*cos(alpha) sin(cta)*sin(alpha) a*cos(cta);
sin(cta) cos(cta)*cos(alpha) -cos(cta)*sin(alpha) a*sin(cta);
0 sin(alpha) cos(alpha) d;
0 0 0 1];
end%% 计算DH矩阵 參數a, alpha, d, ct
function [ans] = MDH(a, alpha, d, cta)
ans = [
cos(cta) -sin(cta) 0 a;
sin(cta)*cos(alpha) cos(cta)*cos(alpha) -sin(alpha) -sin(alpha)*d;
sin(cta)*sin(alpha) cos(cta)*sin(alpha) cos(alpha) cos(alpha)*d;
0 0 0 1];
end5 參考文獻
《机器人学导论:分析控制及应用》(美)尼库 著
《机器人学导论》(美)克来格 著
《机器人学导论》(美)约翰 J 卡雷格 著
《机器人学:建模、规划与控制》布鲁诺·西西里安诺、洛伦索·夏维科、路易吉·维拉尼 、朱塞佩·奥里奥洛 著
《Springer Handbook of Robotics》布鲁诺·西西里安诺、歐莎瑪 哈提卜