【论文阅读笔记】Trained Ternary Quantization
论文发布时间:2016-12
论文地址:https://arxiv.org/pdf/1612.01064.pdf
全文概括
TTQ只量化权重,该方法将权重量化成三元,即2-bit。
与其他方法不同的是,该方法的尺度因子更具有“包容性”,不是某层权重元素绝对值的均值 α l = ∑ ∣ w ∣ c o u n t l \alpha_l=\sum\frac{|w|}{count_l} αl=∑countl∣w∣,而是将正负尺度因子设定为参数(正负尺度都大于零),通过反向传播学习获得。即从 { − α , 0 , α } ⟶ { − W l n , 0 , W l p } \{ -\alpha,0,\alpha\}\longrightarrow\{-W_l^n,0,W_l^p\} {−α,0,α}⟶{−Wln,0,Wlp}。
提出了启发性的稀疏化思想:将最大值的 t t t 倍( t ∈ ( 0 , 1 ) t\in(0,1) t∈(0,1) )作为判断稀疏的阈值,即 w q = 0 ; i f w r ≤ ∣ t w m a x ∣ w_q=0; if\ w_r \leq |tw_{max}| wq=0;if wr≤∣twmax∣。 t t t是超参数。
提出了新的训练结构,其每层的两个尺度因子,直接通过网络模型反向传播学习,而不是通过学习网络参数后统计得到。即反向传播有两条路劲,一条指向全精度权重以学习参数分布,一条指向尺度因子以学习量化“边界”。
得到一个结论:第一个卷积层量化后,两个尺度因子变小,稀疏性更低;而最后一个卷积层和全连接层量化后,两个尺度因子变大,稀疏性更高。(个人猜测,第一层是因为要传播信息,所以分布比较紧凑;最后一层是因为要进行分类,所以大值与小值差距较大)
对尺度因子进行训练的好处在于,正负尺度因子的不对称使得模型能力更强,且针对所有层有一个常数稀疏r,调整超参数r可以调整量化阈值,能够获得不同稀疏度的三值网络。
简介
原来的三元权重网络, { − 1 , 0 , 1 } \{-1,0,1\} {−1,0,1}, { − E , 0 , E } \{-E,0,E\} {−E,0,E}都不是通过学习得到的,而是粗精度地取符号。在本文的三元权重网络,每层有两个参数,得到的网络权重为 { − W l n , 0 , W l p } \{-W_l^n,0,W_l^p\} {−Wln,0,Wlp}。
相关网络
Binary Neural Network(BNN)
该方法使用类似概率的方法将 32-bit 的权重转成 二值/三值 权重: w b ∼ B e r n o u l l i ( w ^ + 1 2 ) ∗ 2 − 1 w^b\sim Bernoulli(\frac{\hat{w}+1}2)*2-1 wb∼Bernoulli(2w^+1)∗2−1 w t ∼ B e r n o u l l i ( ∣ w ^ ∣ ) ∗ s i g n ( ∣ w ^ ∣ ) w^t\sim Bernoulli(|\hat{w}|)*sign(|\hat{w}|) wt∼Bernoulli(∣w^∣)∗sign(∣w^∣) 其中, w ^ \hat{w} w^表示全精度权重。
DoREFA-Net
w b = E ( ∣ w ^ ∣ ) ∗ s i g n ( w ^ ) w^b=E(|\hat{w}|)*sign(\hat{w}) wb=E(∣w^∣)∗sign(w^) 其中, E ( ∣ w ^ ∣ ) E(|\hat{w}|) E(∣w^∣)表示权重绝对值的平均值。
Ternary Weight Networks(TWN)
w l t = { W l w l ^ > Δ l 0 ∣ w l ^ ∣ ≤ Δ l − W l w ^ l < − Δ l w^t_l=\begin{cases}W_l&\hat{w_l}>\Delta_l \\ 0 & |\hat{w_l}|\leq \Delta_l \\ -W_l &\hat{w}_l<-\Delta_l\end{cases} wlt=⎩⎪⎨⎪⎧Wl0−Wlwl^>Δl∣wl^∣≤Δlw^l<−Δl
Δ l = 0.7 ∗ E ( ∣ w l ^ ∣ ) \Delta_l=0.7*E(|\hat{w_l}|) Δl=0.7∗E(∣wl^∣) W l = E i ∈ { i ∣ w l ^ > Δ } ( ∣ w l ( i ) ^ ∣ ) W_l=\mathop{E}\limits_{i\in\{i|\hat{w_l}>\Delta\}}(|\hat{w_l(i)}|) Wl=i∈{i∣wl^>Δ}E(∣wl(i)^∣)
方法介绍
在前向传播时,权重量化如下: w l t = { W l p w l ^ > Δ l 0 ∣ w l ^ ∣ ≤ Δ l − W l n w ^ l < − Δ l w^t_l=\begin{cases}W_l^p&\hat{w_l}>\Delta_l \\ 0 & |\hat{w_l}|\leq \Delta_l \\ -W_l^n &\hat{w}_l<-\Delta_l\end{cases} wlt=⎩⎪⎨⎪⎧Wlp0−Wlnwl^>Δl∣wl^∣≤Δlw^l<−Δl
求导如下: ∂ L ∂ W l p = ∑ i ∈ I l p ∂ L ∂ w l t ( i ) , ∂ L ∂ W l n = ∑ i ∈ I l n ∂ L ∂ w l t ( i ) \frac{\partial L}{\partial W_l^p}=\sum\limits_{i\in I^p_l}\frac{\partial L}{\partial w_l^t(i)},\frac{\partial L}{\partial W_l^n}=\sum\limits_{i\in I^n_l}\frac{\partial L}{\partial w_l^t(i)} ∂Wlp∂L=i∈Ilp∑∂wlt(i)∂L,∂Wln∂L=i∈Iln∑∂wlt(i)∂L 其中, I l p = { i ∣ w l ^ ( i ) > Δ l } I_l^p=\{i|\hat{w_l}(i)>\Delta_l\} Ilp={i∣wl^(i)>Δl}, I l n = { i ∣ w l ^ ( i ) < Δ l } I_l^n=\{i|\hat{w_l}(i)<\Delta_l\} Iln={i∣wl^(i)<Δl}
全精度权重的求导如下: ∂ L ∂ w l ^ = { W l p ∗ ∂ L ∂ w l t w ^ l > Δ l 1 ∗ ∂ L ∂ w l t ∣ w l ^ ∣ ≤ Δ l W l n ∗ ∂ L ∂ w l t w ^ l < − Δ l \frac{\partial L}{\partial \hat{w_l}}=\begin{cases}W_l^p*\frac{\partial L}{\partial w_l^t} & \hat{w}_l>\Delta_l \\ 1* \frac{\partial L}{\partial w_l^t} &|\hat{w_l}|\leq \Delta_l \\ W_l^n*\frac{\partial L}{\partial w_l^t} & \hat{w}_l<-\Delta_l \end{cases} ∂wl^∂L=⎩⎪⎪⎨⎪⎪⎧Wlp∗∂wlt∂L1∗∂wlt∂LWln∗∂wlt∂Lw^l>Δl∣wl^∣≤Δlw^l<−Δl
阈值: Δ l = t ∗ m a x ( ∣ w ^ ∣ ) \Delta_l=t*\mathop{max}(|\hat{w}|) Δl=t∗max(∣w^∣) 在 CIFAR-10数据集中, t 设为 0.05 0.05 0.05。
实验
CIFAR-10
初始学习率设为 0.1 0.1 0.1,在80、120、300个周期时乘以 0.1 0.1 0.1;L2正则化权重衰减设为 0.0002 0.0002 0.0002。一般 160 160 160个周期就能收敛。
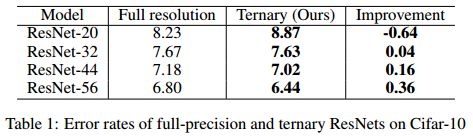
ImageNet
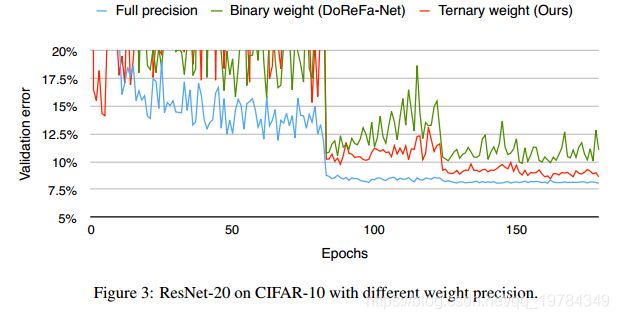
batch_size设为128;初始学习率设为10-4,每56个周期乘以0.2;L2权重衰减设为5*10-6;大概在64个周期时,就比其他 low-bit 网络要好了。