数据结构:并查集 Union-Find算法(不相交集)原理及C++实现
前言:
这一次为大家介绍的另外一种比较基础的算法——并查集Union-Find算法。这是一种用于不相交集(
Disjoint Sets)的查询以及合并问题的算法。主要用树的形式来进行链接,这里我们将使用的是数组来表现。
PS:不相交集是并查集的另一个说法~~
还是老样子,先是 GitHub传送门~~
原理:
首先我们要认识到并查集算法是用来处理不相交集问题的一个工具,它为等价关系的确定提供了很大的便利。
并查集中的Union可以将集合进行链接,使它们成为等价类;而Find可以查找集合的类别,从而直观的了解其等价关系。而我们对等价关系有严格的定义,先看看什么是等价关系吧。
等价关系:
等价关系 R 要求处于同一个等价类S中的任意元素a,b满足三点要求:
1.自反性,对于所有的a属于S,有aRa;
2.对称性,若aRb则有bRa;
3.传递性,若aRb,bRc,则有aRc;
这样似乎很模糊,对于没有学过离散数学的朋友来说等价的概念仍然不清楚,那我就举两个例子,第一个就是
“=”关系;这是一个最经典的等价关系它满足:自反性—— 1 = 1成立;对称性——若 a = b,则b = a;传递性——若a = b,b = c,那么a = c;不知道这样理解了吗?
如果还没有的话那就在举一个例子吧,有三个人分别是小A,小B和小C,现在有一个关系为“某人和某人是一个学院的”;现在我们就来判断这个关系是不是一个等价关系;首先我们来
判断自反性——小A和小A是一个学院的吗?答案显而易见,那么
自反性满足!接下来是
对称性判断——如果我们知道了小A和小B是一个学院的,那么小B和小A是一个学院的吗?肯定是的啊;最后就是
传递性判断了——若小A和小B一个学院,小B和小C一个学院那么我们也可以知道小A和小C一个学院!那么
“某人和某人是一个学院的”就是一个等价关系!
所以判断一个关系是不是等价关系就需要对这三个性质进行判断,
若有一个不满足,则不是等价关系!比如“<=”关系,因为他不满足对称性,即a<=b不能得出b<=a!
等价类:
等价类即为一个集合,在这个集合中的所有元素之间都满足等价关系,比如对于之前的“某人和某人是一个学院的”关系来将,计算机学院的所有学生就是一个等价类,物理学院的所有学生也是一个等价类,而学校的所有学生对于这个关系就不是等价类了!
Union:
Union功能是用于创建等价关系的,即若对于两个不相干的元素或集合A,B,若执行Union(A, B)则会在AB间创建等价关系,而在实际的代码编写中,我们
使用树的思想但用数组来实现Union功能!但接下来我们还是具体看看Union操作吧:
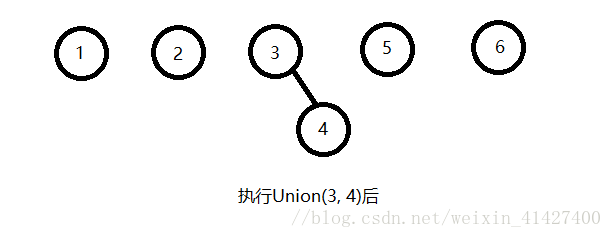
假设我们开始是有毫不相干的六个元素1,2 ,......,5,6,他们之间没有任何关系,也就是说他们都是独立的!
接下来我们如果发现3和4之间满足等价关系,那么进行一次Union(3, 4)的操作,就会得到下图中的样子;
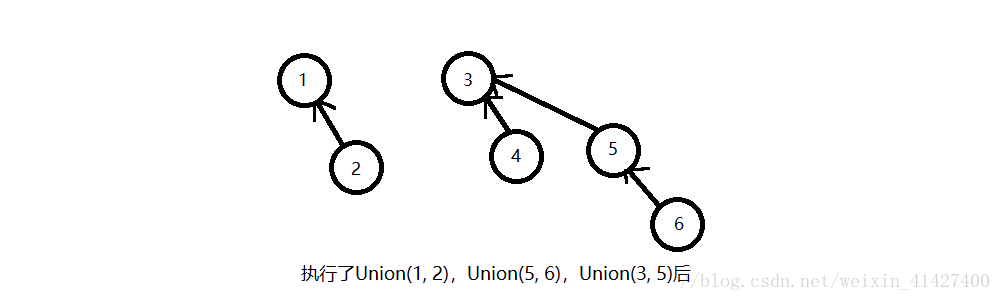
接下来我们又发现了许多等价关系,依次执行了Union(1, 2),Union(5, 6),Union(3, 5)
执行了这些操作后,集合变成了这个样子,可以发现1,2在一个等价类中,其他元素在另外一个等价类中;这里就要注意啦,因为我们
如果把这个图看做一个树,那么1,3就是树根,而2是1的一个儿子,4,5是3的儿子,6是5的儿子,这不正是树吗。这就是我们
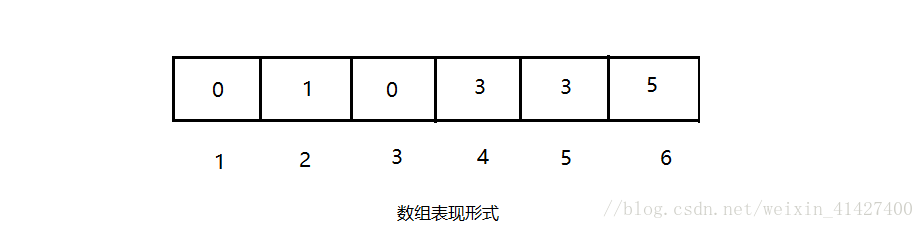
使用树的思想!那么怎么用数组表示呢?我们约定数组S,那么
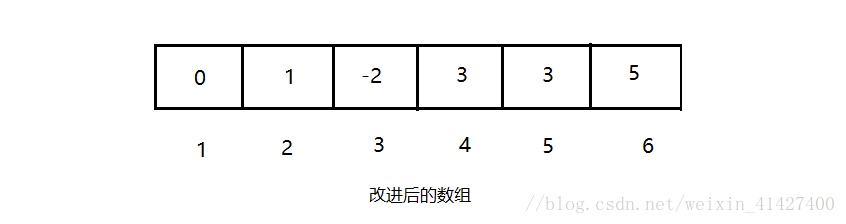
S[x]就是元素x的父节点,如果这个元素时树根,那么规定S[x]=0,这样一来上面这棵树就可以表示为下图:
这样一来我们就使用了数组来实现!那么编写代码也就是很简单的事情了,首先是一个简单的Union实现:
void Disjoint_Set::SetUnion(SetType Root1, SetType Root2) {
DisjSet[Root2] = Root1;
}
这个函数很简单,就是
把元素Root1变为Root2的父节点(树的思想),实际操作中就是令S[Root2]=Root1;
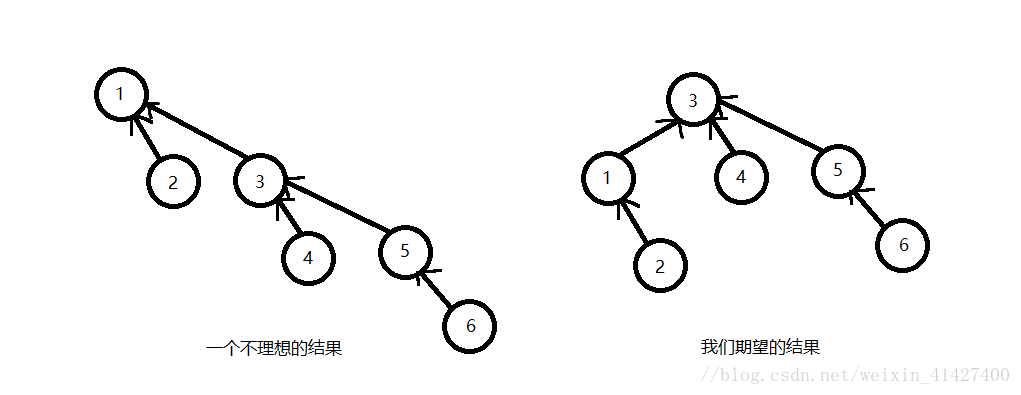
如果没有什么效率的追求,那么Union这样写也没问题,但是我们显然不可能这样,因为上述的Union只是单纯的将Root2作为Root1的子节点处理,这很容易加深树的深度,大家都知道,树的深度越深,那么执行操作的时间也就越长,在上图的树中再执行一次Union(1, 3),得到的结果显然与我们的期望不同!
我们期望它可以将1作为3的子树而不是反过来,我们总是希望深度更深(高度更高)的树可以作为树根,而不是儿子,但是很多时候我们并不知道他们的具体情况,那么我们该怎么办呢,这里我们给出了更好的一种方法,那就是在树根处记录树的深度!那么数组就会变成下图所示:
可以发现我们只是在树根处做出了改进,让树根储存树高度的负值,这样我们就可以通过检索到树根,比较树的高度后再进行Union操作,以下是改进后的代码:
void Disjoint_Set::SetUnion(SetType Root1, SetType Root2) {
// 找到对应元素所在集合的根部
Root1 = Find(Root1);
Root2 = Find(Root2);
// case1:当Root2集合高度大于Root1时
if (DisjSet[Root2] < DisjSet[Root2])
DisjSet[Root1] = Root2; // 将Root1合并到Root2中
else {
// case2:当Root1集合高度等于Root2时
if (DisjSet[Root1] == DisjSet[Root2])
DisjSet[Root1]--; // 加深Root1高度
// case3:当Root1集合高度大于Root2时
// 将Root2合并到Root1上
DisjSet[Root2] = Root1;
}
}
注意:
在树合并以后,如果合并的两棵树深度相同,主树的深度会加深;其中用到的Find是接下来介绍的功能,目的是返回元素所在的集合,可以看下文;
Find:
Find功能是并查集的另外一个功能,目的是返回一个元素所在的集合;从Union的介绍中我们可以看出来,
一个等价类就是一棵树,那么我们
返回集合也就可以变成返回一个树的树根;这样就很简单了,接下来是Find的简单实现:
SetType Disjoint_Set::Find(int X) {
// 判断是否是根部
if (DisjSet[X] <= 0)
return X;
else
return Find(DisjSet[X]);
}
我们可以发现,在执行改进后的Find(6)后,树的高度减少了,这是因为6的根变为了5的根,而5的根变为了3的根1,这样他们都直接与1链接了!接下来是具体的代码:
SetType Disjoint_Set::Find(int X) {
// 判断是否是根部
if (DisjSet[X] <= 0)
return X;
else
return DisjSet[X] = Find(DisjSet[X]);
}
可以看见我们只做了一点小小的改进就得到了我们想要的效果,是不是很神奇!
应用:
关于并查集的一个具体应用可已在Kruskal算法中发现,而这可以在我的 另外一篇博客中找到哦~~
C++实现:
最后我将给出完整代码啦,先是.h文件:
#ifndef DISJOINT_SET_H
#define DISJOINT_SET_H
#include
#include
using namespace std;
// 重定义变量名,便于操作与辨认用途
typedef int SetType;
/* Disjoint_Set类(不相交集)
* 接口:
* Find:查找功能:查找对应元素所对应的集合
* SetUnion:联合功能:将对应两个元素所在的集合链接
*/
class Disjoint_Set
{
public:
// 构造函数
Disjoint_Set(int = 10);
// 析构函数
~Disjoint_Set();
// 接口函数
SetType Find(int);
void SetUnion(SetType, SetType);
private:
int NumSets; // 储存总集合中元素的个数
int *DisjSet; // 储存等价类森林
};
#endif
然后就是.cpp文件了:
#include "Disjoint_Set.h"
/* 构造函数:初始化对象
* 返回值:无
* 参数:nums:整个集合中元素的个数
*/
Disjoint_Set::Disjoint_Set(int nums)
: NumSets(nums){
DisjSet = new int[NumSets + 1]; // 申请不相交集森林的存储空间
if (DisjSet == NULL)
cout << "不相交集申请失败!" << endl;
// 初始化森林中的每棵树
else
for (int i = NumSets; i > 0; i--)
DisjSet[i] = 0;
}
/* 析构函数:对象消亡时回收存储空间
* 返回值:无
* 参数:无
*/
Disjoint_Set::~Disjoint_Set()
{
delete DisjSet;
DisjSet = NULL;
}
/* (不是最好的方法)
* 联合函数:将两个集合链接
* 返回值:无
* 参数:Root1:想要合并的一个集合;Root2:想要合并的另一个集合
void Disjoint_Set::SetUnion(SetType Root1, SetType Root2) {
DisjSet[Root2] = Root1;
}
*/
/* 联合函数:将两个集合链接
* 返回值 : 无
* 参数 : Root1 : 想要合并的一个集合;Root2 : 想要合并的另一个集合
*/
void Disjoint_Set::SetUnion(SetType Root1, SetType Root2) {
// 找到对应元素所在集合的根部
Root1 = Find(Root1);
Root2 = Find(Root2);
// case1:当Root2集合高度大于Root1时
if (DisjSet[Root2] < DisjSet[Root2])
DisjSet[Root1] = Root2; // 将Root1合并到Root2中
else {
// case2:当Root1集合高度等于Root2时
if (DisjSet[Root1] == DisjSet[Root2])
DisjSet[Root1]--; // 加深Root1高度
// case3:当Root1集合高度大于Root2时
// 将Root2合并到Root1上
DisjSet[Root2] = Root1;
}
}
/* 查找函数:查找对应元素所在的集合
* 返回值:SetTpye:对应元素所在集合的根
* 参数:X:想要查找的元素
*/
SetType Disjoint_Set::Find(int X) {
// 判断是否是根部
if (DisjSet[X] <= 0)
return X;
// 继续寻找根部
// 同时进行路径压缩:
// 将中途检索到的每一个节点的父节点都变为根;
// 注意:此处不用重新计算高度!虽然高度会改变,但是我们
// 使用估计高度(或称为秩--rank);
else
return DisjSet[X] = Find(DisjSet[X]);
}
最后转载请注明出处哦~~
参考文献:《数据结构与算法分析——C语言描述》