本系列是台湾大学资讯工程系林軒田(Hsuan-Tien Lin)教授开设的《机器学习基石》课程的梳理。重在梳理,而非详细的笔记,因此可能会略去一些细节。
该课程共16讲,分为4个部分:
- 机器什么时候能够学习?(When Can Machines Learn?)
- 机器为什么能够学习?(Why Can Machines Learn?)
- 机器怎样学习?(How Can Machines Learn?)
- 机器怎样可以学得更好?(How Can Machines Learn Better?)
本文是第2部分,对应原课程中的4-8讲。
本部分的主要内容:
- 用案例引出学习可行性的疑问;
- 详细介绍VC维理论,它给出了机器学习的可靠性保证;
- 介绍误差的度量,以及对误差权重不同的情况的处理方法。
1 学习可行性的疑问
先来一个小学奥数题/公务员考试题:
其实这个题没有标准答案,以下两种解答都是对的:
- 对称为\(+1\),非对称为\(-1\),因此答案是\(+1\);
- 最左上角的格子白色为\(+1\),黑色为\(-1\),因此答案是\(-1\);
因此,选择不同的规则,你会获得不同的答案。那么,如果给你一些历史数据,机器学习出某种规则,是否也会遇到这样的情况呢?
2 机器学习的可靠性保证
2.1 Hoeffding不等式
来看另一个问题:有一个罐子,里面装有许许多多黄色和绿色的小球,该如何估计黄球的比例?
很简单,抽样就行了。抽出一部分样本,计算得到样本中的黄球比例\(\nu\),用这个比例作为罐子中的黄球比例\(\mu\)的估计即可。这样的估计准不准呢?在统计学中,有Hoeffding不等式给出准确率的界限:
其中\(N\)为抽样的样本个数。这个式子的意思是,\(\nu\)和\(\mu\)相差较远的概率会有一个上限,在大样本下,这个上限会比较小,因此\(\nu=\mu\)可以叫做概率近似正确(PAC,probably approximately correct)。
2.2 机器学习中的Hoeffding不等式
现在将这个过程类比到机器学习中。罐子中的小球对应于\(\mathcal{X}\)中的单个数据\(\mathbf{x}\),给定假设集中的一个假设\(h\),罐子中黄球的比例就对应于\(\mathcal{X}\)中使得\(h(\mathbf{x})=f(\mathbf{x})\)的\(\mathbf{x}\)的比例。现在抽取出一部分样本,这个样本对应于现有的数据集\(\mathcal{D}\),我们可以很容易地知道对\(\mathcal{D}\)中每一个数据\((\mathbf{x}_n,y_n)\)是否有\(h(\mathbf{x}_n)=y_n\),若相等,对应的小球为黄色,反之为绿色。我们的目的,是要知道在整个\(\mathcal{X}\)中满足\(h(\mathbf{x})=f(\mathbf{x})\)的\(\mathbf{x}\)的比例有多少。
若\(N\)足够大,且\(\mathbf{x}_n\)为i.i.d.,对于某个固定的\(h\)来说,就可以用已知的\(E_{\text{in}}(h)=\dfrac{1}{N}\sum\limits_{n=1}^{N} \mathbf{1}_{[h(\mathbf{x}_n)\ne y_n]}\)去推断\(E_{\text{out}}(h)=\mathop{\mathcal{E}}\limits_{\mathbf{x}\sim P}\mathbf{1}_{[h(\mathbf{x})\ne f(\mathbf{x})]}\),从而判断该\(h\)的表现如何,如下图:
根据Hoeffding不等式,就是
如果\(E_{\text{in}}(h)\)和\(E_{\text{out}}(h)\)足够接近,并且\(E_{\text{in}}(h)\)足够小,这就能保证\(E_{\text{out}}(h)\)足够小,也就能判断出对于抽样过程\(P\),有\(h\approx f\)。
但是,这只能用来判断某个\(h\)是否足够好。如果现在是用算法\(\mathcal{A}\)从假设集\(\mathcal{H}\)中选出一个\(h\),再套用上面的不等式,就会有问题。试想一下,假设有150个人,每人丢5次硬币,就有超过99%的概率会出现有某个丢5次硬币都是正面的人,这能说明他的丢硬币技术比其他人高吗?如果选择他作为我们的“\(g\)”,能保证他以后再去丢硬币,得到正面的概率也比其他人更大吗?
同理,如果是从\(\mathcal{H}\)中选出一个在样本\(\mathcal{D}\)内误差最小的\(g\),能保证它在\(\mathcal{D}\)外也是更好的吗?想要得到这样的保证,还需对不等式做一些修正。
对每个\(h\),都可能会有一些\(\mathcal{D}\),使得\(h\)在它上面的\(E_{\text{in}}(h)\)和真正的\(E_{\text{out}}(h)\)相差很大,把这种\(\mathcal{D}\)称作“坏的”,Hoeffding不等式本质上是保证抽到坏的\(\mathcal{D}\)的概率有一个上限。记\(\vert\mathcal{H}\vert=M\),即共有\(M\)个\(h\),我们想要保证的是不管最后\(\mathcal{A}\)选出了哪个,\(\mathcal{D}\)是“坏的”的概率都有较小的上限,因此,要计算的应该是对至少一个\(h\)来说\(\mathcal{D}\)是“坏的”的概率:
这才是\(\mathcal{A}\)选出来的\(h\)的\(E_{\text{in}}(h)\)和\(E_{\text{out}}(h)\)距离的上限。但在上面的过程中,因为对事件的并集直接用了加的运算,这个上限被放得太大了,由于不同的\(h\)对应的“坏的”\(\mathcal{D}\)很可能有很大重叠,因此真实的上限应该要小得多。如图:
另外,\(M\)如果是有限的,根据上式,我们还是可以通过增大\(N\)来保证\(E_{\text{in}}(h)\)和\(E_{\text{out}}(h)\)足够接近,但如果\(M\)是无限的呢?如在PLA中,系数的取值就可以是无限多个,因此PLA的\(M\)是无穷大的。
2.3 VC维
\(M\)为无穷大时,还是有办法的。尽管PLA的\(M\)是无穷大,但其实,我们可以对它的\(\mathcal{H}\)中的元素进行分类,只要样本个数是有限的,它的类别就是有限的。比如在只有一个样本的情况中,二维PLA的\(\mathcal{H}\)中的元素(就是二维平面上的所有直线)可以简单分为两类,一类是把该样本点分为正的,一类是把该样本点分为负的:
而在两个样本的情况中,\(\mathcal{H}\)中的元素可以分为4类:
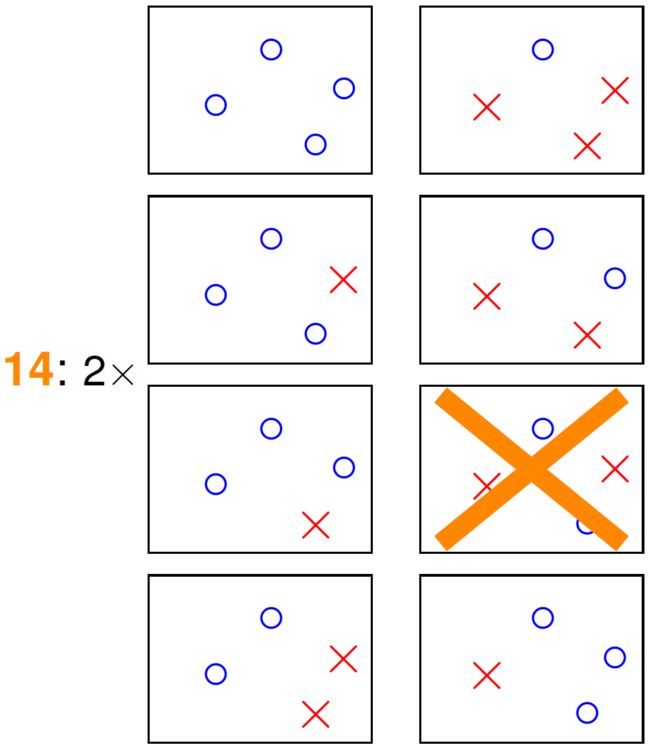
而当有4个样本时,\(\mathcal{H}\)中的元素最多只能分成14类:
这说明,在PLA中,有\(N\)个样本时,有效的\(M\)会小于等于\(2^N\)。
接下来,引入几个概念:
- 二分(Dichotomies):对\(N\)个样本,每个样本都有正负两种可能,将所有样本组成的每一种可能称为一个dichotomy,dichotomies的集合可记为\(\mathcal{H}(\mathbf{x}_1, \mathbf{x}_2, \ldots,\mathbf{x}_N)\),显然,集合中元素个数的上限是\(2^N\);
- 成长函数(Growth Function):定义成长函数\(m_{\mathcal{H}}(N)=\max\limits_{\mathbf{x}_1, \mathbf{x}_2, \ldots,\mathbf{x}_N \in \mathcal{X}} \vert \mathcal{H}(\mathbf{x}_1, \mathbf{x}_2, \ldots,\mathbf{x}_N) \vert\),它的上限是\(2^N\),对于大多数模型(如二维感知机)的\(\mathcal{H}\)来说,\(m_{\mathcal{H}}(N)\)比\(2^N\)小,仅为多项式大小;
- 打散(Shatter):如果\(\mathcal{H}\)可以完全实现\(N\)个样本的\(2^N\)种dichotomies,则称\(N\)个点可被\(\mathcal{H}\)打散;
- 突破点(Break Point):若\(k\)个点无论如何也无法被\(\mathcal{H}\)打散,则称\(k\)为\(\mathcal{H}\)的break point,根据定义,所有比\(k\)大的整数也都会成为break points,对于二维感知机来说,从4开始就是它的break point。
接下来就是要找到,break point和\(m_{\mathcal{H}}(N)\)的关系。
我们继续引入界限函数(Bounding Function)的概念:\(B(N,k)\),它是当最小的break point为\(k\)时的最大可能\(m_{\mathcal{H}}(N)\)。那么,该如何计算它或者它的上限?
首先,当\(k=2\)时,表示任意两个点都不能被打散,因此当\(N=2\)时有\(B(2,2)=3\),即最多能列举出3种dichotomies(4种就是这两个点被打散了),当\(N=3\)时有\(B(3,2)=4\)(穷举法可知)。而当\(k=1\)时,由于任何一个点都不能被打散,因此只能有一种dichotomy,即\(B(N,1)=1\)。另外,如果\(k>N\),由于小于\(k\)个样本点都能被打散,因此会有\(B(N,k)=2^N\)。而如果\(N=k\),那么只需在\(2^N\)个被打散的点中拿掉一种dichotomy,就能满足这\(N\)个点不被打散的概念了,因此有\(B(N,k)=2^N-1\)。
到目前为止,在下面这张函数表中还有一部分没有计算:
不妨先来看\(B(4,3)\)该如何计算。如果用穷举法,可以得出\(B(4,3)=11\):
观察这11种dichotomies发现,它们可以分成两组,其中一组的前3个点是有重复的,它们成为不同的dichotomies仅仅是因为\(\mathbf{x}_4\)不同,而另一组的前3个点没有重复。
如果把前3个点有重复的8种dichotomies记为\(2\alpha\)(只看前3个点就是\(\alpha\)种),后3种记为\(\beta\),那么就有\(2\alpha+\beta=11\)。而其实,\(B(4,3)\)无非就是比\(B(3,\cdot)\)多了一个点,假设现在把最后一个点去掉,那么前3个点只可能有\(\alpha+\beta\)种dichotomies(因为第一组\(2\alpha\)种是前面3个点各重复两次,因此需要剔除一半),由于\(B(4,3)\)中任意3个点都不能被打散,因此前3个点也必须不能被打散,所以有\(\alpha+\beta\le B(3,3)\)。
另一方面,由于\(2\alpha\)组中的4个点中,任意3个点都不能被打散,而第4个点是在每一组前3个点固定的情况下取正/负,因此前3个点中的任意2个点都不能被打散(否则在加入第4个点后就会有3个点被打散)。因此,必须要保证\(\alpha\le B(3,2)\)。
由此可知,\(B(4,3)=2\alpha+\beta \le B(3,3)+B(3,2)\),以此类推,有\(B(N,k)\le B(N-1,k)+B(N-1,k-1)\),最终结果如图:
用数学归纳法即可证明:\(B(N,k)\le \sum\limits_{i=0}^{k-1}\binom{N}{i}\),具体过程在此略过。事实上,可以证明得\(B(N,k)=\sum\limits_{i=0}^{k-1}\binom{N}{i}\),具体的数学过程较复杂,课程中也略过了。该式说明,\(B(N,k)\)中成长最快的一项最多就是\(N^{k-1}\)的成长速度。
由\(B(N,k)\)的定义,只要break point \(k\)存在,那么\(m_{\mathcal{H}}(N)\)的上限就是\(B(N,k)\),也因此,\(m_{\mathcal{H}}(N)\)中成长最快的一项最多就是\(N^{k-1}\)的成长速度。
在有了\(m_{\mathcal{H}}(N)\)后,想用它取代\(M\),还需要做一些处理,具体在此略过。最后可以得到的是Vapnik-Chervonenkis(VC) bound:
定义VC维(VC dimension)\(d_{\text{vc}}(\mathcal{H})\)为满足\(m_{\mathcal{H}}(N)=2^N\)的最大的\(N\),也即\(\mathcal{H}\)能打散的最大的点的个数,或最小的break point减1。当\(N\ge2\)且\(d_{\text{vc}}\ge 2\)时,有\(m_{\mathcal{H}}(N)\le N^{d_{\text{vc}}}\)。
对于\(d\)维感知机模型来说,有\(d_{\text{vc}}=d+1\)(证明略)。只要\(d_{\text{vc}}\)是有限的,就可以完成泛化。\(d_{\text{vc}}(\mathcal{H})\)就相当于是\(\mathcal{H}\)的powerfulness。
2.4 VC Bound与模型复杂度惩罚
对于\(g=\mathcal{A}(\mathcal{D})\in \mathcal{H}\),如果\(\mathcal{D}\)在统计上足够大,有
不等式左侧表示“坏的”的几率。若将不等式右边记为\(\delta\),可将\(\epsilon\)反表示为\(\epsilon=\sqrt{\dfrac{8}{N}\ln{\dfrac{4(2N)^{d_{\text{vc}}}}{\delta}}}=\Omega(N,\mathcal{H},\delta)\),\(\Omega(N,\mathcal{H},\delta)\)就代表了对模型复杂度的惩罚。
可以看出,至少有\(1-\delta\)的概率,能满足
\(d_{\text{vc}}\)和error的关系如下图:
要找到最优的\(d_{\text{vc}}\),才能使error最小。
VC Bound只是一个非常宽松的理论界限。比如设定\(\epsilon=0.1\),\(\delta=0.1\),\(d_{\text{vc}}=3\),那么根据前式,可得到\(N\approx 10,000 d_{\text{vc}}\),但在实践中,往往只需要\(N\approx 10 d_{\text{vc}}\)的数据量就够了。
2.5 有噪声时的VC Bound
如果标签被打错了,或是同一个人被打了不同标签,又或是\(\mathbf{x}\)的信息不准确,都会引入噪声。在有噪声时,VC Bound依旧有效吗?
回到之前小球的例子,之前的小球,每个小球的颜色都是确定的,这种情况叫做是“deterministic”的,在有噪声的情况中,可以认为每个小球的颜色服从某种概率,即\(y\sim P(y|\mathbf{x})\),这叫做是“probabilistic”的。可以证明如果\((\mathbf{x},y)\mathop{\sim}^{i.i.d.}P(\mathbf{x},y)\),那么VC理论依旧是有效的。
有噪声时,学习的目标是在常见的样本\(P(\mathbf{x})\)上,学习\(P(y|\mathbf{x})\)。新的学习流程如下:

VC理论依旧有效,pocket算法就是个很好的例子。
3 误差度量
在这里介绍一种逐点的误差度量(pointwise error measure),可以表达成\(\text{err}(g(\mathbf{x}), f(\mathbf{x}))\),\(g(\mathbf{x})\)可记为\(\tilde{y}\),\(f(\mathbf{x})\)可记为y。
有两种比较重要的pointwise error measure:
- \(\text{err}(\tilde{y}, y)=\mathbb{1}_{[\tilde{y} \ne y]}\),这一般用在分类问题中;
- \(\text{err}(\tilde{y}, y)=(\tilde{y} - y)^2\),这一般用在回归问题中。
在分类问题中,错误可分为两类,如下图所示:
根据这两类错误的重要性不同,可以对它们赋予不同的权重。因此,不同的应用可以有不同的\(\text{err}\)。在算法中考虑误差度量时(记用在算法中的错误度量为\(\widehat{\text{err}}\)),最好的情况当然是直接令\(\widehat{\text{err}}=\text{err}\),但这可能会导致很难计算,比如会带来NP-hard问题等,一般来说,最好要设计一个对于\(\mathcal{A}\)来说能比较容易进行最优化的\(\widehat{\text{err}}\),最好要有闭式解(closed-form solution)或有凸的目标函数。
在\(\mathcal{A}\)中加入误差度量的设计后,学习流程如下:
对于两类错误权重不同的情况,可以用“virtual copying”的策略去学习。以pocket算法为例,假设false reject错误的权重为1,false accept错误的权重为1000,在计算时不必真的对每个样本点赋予权重,可以“虚拟地”将\(y=-1\)的点复制1000份。在实践中,也不必真的复制,可以在随机选择样本点时,让算法随机选出\(y=-1\)的点的概率增大1000倍即可。