二值网络
本文转载于二值神经网络（Binary Neural Network，BNN）
BNN算法
要想使整个神经网络二值化，那么最需要解决的问题就是反向传播时的求导。下面会通过一系列手段使的这个操作可行。
二值化手段
直觉上看，二值化的手段非常简单啊，整数是1，负数是-1就可以了。但实际上，这只是其中一种，即决定式的二值化。
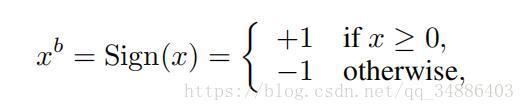
还有一种是随机式的二值化
这个样的公式让我想起跟一个大神聊天时谈到的问题，比如，在我之前Google点击率预估那篇博文中提到的一种网络压缩方法，即不适用32bit的浮点数而是使用16bit格式的数字。既然有压缩，那么就会遇到精度问题，比如如果压缩后的数值表示精度能到0.01，而更新的梯度的值没到这个精度，比如0.001，此时该如何更新这个值？
答案就是用一定的概率去更新这个值
第二种方法虽然看起来比第一种更合理，但是在实现时却有一个问题，那就是每次生成随机数会非常耗时，所以一般使用第一种方法。
梯度计算和累加
虽然BNN的参数和各层的激活值是二值化的，但由于两个原因，导致梯度不得不用较高精度的实数而不是二值进行存储。两个原因如下：
- 梯度的值的量级很小
- 梯度具有累加效果，即梯度都带有一定的噪音，而噪音一般认为是服从正态分布的，所以，多次累加梯度才能把噪音平均消耗掉
另一方面，二值化相当于给权重和激活值添加了噪声，而这样的噪声具有正则化作用，可以防止模型过拟合。所以，二值化也可以被看做是Dropout的一种变形，Dropout是将激活值的一般变成0，从而造成一定的稀疏性，而二值化则是将另一半变成1，从而可以看做是进一步的dropout。
离散化梯度传播
直接对决定式的二值化函数求导的话，那么求导后的值都是0。所以只能采用一种妥协方法，将sign(x)进行宽松。这样，函数就变成可以求导的了。
假设，损失函数是C，二值化操作函数如下：
如果C对q求导已经得到了，那么C对r的求导计算公式如下：
其中 1 ∣ r ∣ ≤ 1 1_{|r|}\le1 1∣r∣≤1的计算公式就是Htanh。
在具体的算法使用中，对于隐含层单元：
- 直接使用决定式的二值化函数得到二值化的激活值。
- 对于权重：
1.在进行参数更新时，要时时刻刻把超出[-1,1]的部分给裁剪了。即权重参数始终是[-1,1]之间的实数。
2.在使用参数是，要将参数进行二值化。
BNN的训练过程
前面的几条技巧，就可以解决求导的问题了。普通卷积神经网络加上BatchNormalization再加上二值化后的模型训练流程如下：
优化技巧
Shift based Batch Normalization
Batch Normalization，简称BN。所谓的BN是指在数据经过一层进入下一层之前，需要对数据进行归一化，使之均值为0，方差为1。这样可以使得各层的参数量级上没有太大的差别。
有三个优点：
- 加速训练
- 减小权重的值的尺度的影响
- 归一化所带来的噪声也有模型正则化的作用
但是，BN有一个缺点，那就是在训练时，因为要对数据进行scale，所以有很多矩阵乘法，导致训练时间过长。
但是，BN有一个缺点，那就是在训练时，因为要对数据进行scale，所以有很多矩阵乘法，导致训练时间过长。
Shift based AdaMax
Adam是一种学习规则，学习规则中最普通的就是SGD，关于Adam的原始论文我倒是还没有读过，且把shift based Adamax的算法列出来吧。
第一层
尽管所有的层次的激活和参数都是二值化的，但第一层的输入却是连续值的，因为是像素。若要整个网络都是二值化的，只需将输入变化一下即可。
使用8位数字来表示一个像素，那么输入就是一个img_height×img_width×8的向量，而权重参数是一个img_height×img_width的全1向量。
第一层的计算操作如下：
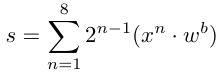
这个函数就把像素值还原回来了，xn的意思我理解是每个数都取第n位。这样累加之后，所有的像素值都被还原了.
这样，各层的计算方法如下：
性能分析
时间复杂度可以降低60%。
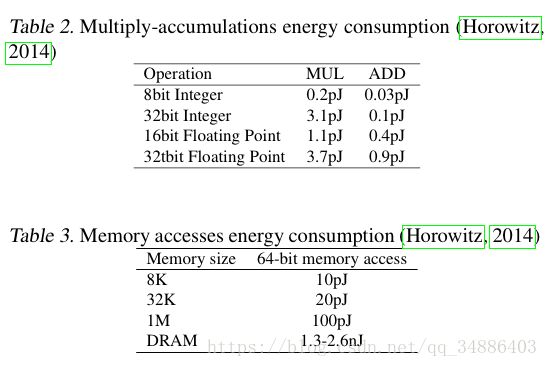
内存和计算耗能
- 内存访问耗时比计算耗时要多
- 相对于32bit的DNN，BNN内存需求量减少为原来的1/32还少，使得能源使用减少31/32。
XNOR-Count
- BNN中计算都变成位运算，一个32bit的乘法损耗200个单位，而一个位操作之损耗1个单位。
Filter数目
- 二值化的不同的卷积核的个数由卷积核的大小决定，比如，3×3的卷积核的数目为 2 9 = 512 2^9=512 29=512个。但是这并不能限制每一层feature_map的数目，因为，卷积核参数是用4D矩阵来存储的，即 M i ∗ M i − 1 ∗ k ∗ k M_i*M_{i-1}*k*k Mi∗Mi−1∗k∗k，相当于第i-1层的每一个feature_map都对应512个不一样的filter，所以Filter数目的上限是 2 k ∗ k ∗ M i − 1 2^{k*k*M_{i-1}} 2k∗k∗Mi−1个。
- 对于卷积核来说，完全相反的卷积核也属于同一类，比如[-1,1,-1]和[1,-1,1]，因为，不同的卷积核的数目可以降低为原来的42%。
实现优化
- 对于位操作而言，可以使用SWAR中的SIMD并行化指令来进行加速。即将32个二值化变量存储在一个32位的寄存器中，从而获得32倍的加速。
- 神经网络的传播过程中，可以使用SWAR技术来使用3个指令计算32个Connection，如下，从而原先32个时间单元的事情现在（accumulation，popcount，xnor）=1+4+1=6个单元就可以完成，提升5.3倍
为了验证上述理论，实现了两个GPU计算核，一个是没有优化的乘法（baseline），一个是使用上面公式的SWAR技术实现的（XNOR）。结果如下：
XNOR相对于baseline快23倍
XNOR相对于cuBLAS快3.4倍
实验设置及结果
实验结果一言以蔽之，就是比最好的结果要稍差，但差的不会太多。
Mnist
Theano设置
- 3个4096维的隐含层
- L2-SVM的输出层
- 使用Dropout
- ADAM学习法则
- 指数衰减的步长
- mini-batch为100的BN
- 训练集的最后10k样本作为验证集来early-stopping和模型选择
- 大概1000次迭代后模型最好，没有在验证集上重新训练。
Torch7设置
与上面设置的区别：
- 没有dropout
- 隐含层数目变为2048
- 使用shift-based AdaMax和BN
- 每十次迭代步长一次右移位
Cifar10
Theano设置
- 没有任何的数据预处理
- 网络结构和Courbariaux 2015的结构一样，除了增加了binarization
- ADAM学习法则
- 步长指数损失
- 参数初始化来自Glorot & Bengio的工作
- mini-batch为50的BN
- 5000个样本作为验证集
- 500次迭代后得到最好效果，没有在验证集上重新训练
Torch7设置
与上面设置的不同：
- 使用shift-based AdaMax和BN（mini-batch大小200）
- 每50次迭代，学习率右移一位。
SVHN
设置
基本与cifar10的设置相同，区别如下：
- 卷积层只使用一半的单元。
- 训练200次迭代就停了，因为太大。
实验结果
总结：
缺点：BNN在训练过程中仍然需要保存实数的参数，这是整个计算的瓶颈。