使用Lucy-Richardson算法去模糊复原图像
Deblurring Images Using the Lucy-Richardson Algorithm
本例展示如何使用Lucy-Richardson算法去模糊图像。 当点扩散函数PSF(模糊运算符)是已知的时候,它可以被有效地使用,但是很少或没有信息可用于噪声。 模糊和噪声图像通过迭代,加速,衰减的Lucy-Richardson算法恢复。 您可以使用光学系统的特性作为输入参数来提高图像恢复的质量。
Step 1: Read Image
该示例读取RGB图像并将其裁剪为256×256×3。 deconvlucy函数可以处理任何维度的数组。
I = imread('board.tif'); I = I(50+(1:256),2+(1:256),:); figure; imshow(I); title('Original Image'); text(size(I,2),size(I,1)+15, ... 'Image courtesy of courtesy of Alexander V. Panasyuk, Ph.D.', ... 'FontSize',7,'HorizontalAlignment','right'); text(size(I,2),size(I,1)+25, ... 'Harvard-Smithsonian Center for Astrophysics', ... 'FontSize',7,'HorizontalAlignment','right');
Step 2: Simulate a Blur and Noise
模拟由于相机运动或对焦不足而可能模糊的真实图像。 由于随机干扰,图像也可能会产生噪音。 该示例通过将高斯滤波器与真实图像进行卷积来模拟模糊(使用imfilter)。 高斯滤波器然后表示点扩散函数PSF。
PSF = fspecial('gaussian',5,5); Blurred = imfilter(I,PSF,'symmetric','conv'); figure; imshow(Blurred); title('Blurred');
该示例通过向模糊图像添加方差V的高斯噪声(使用imnoise)来模拟噪声。 噪声方差V稍后用于定义算法的阻尼参数。
V = .002; BlurredNoisy = imnoise(Blurred,'gaussian',0,V); figure; imshow(BlurredNoisy); title('Blurred & Noisy');
Step 3: Restore the Blurred and Noisy Image
恢复提供PSF的模糊和噪声图像,并仅使用5次迭代(默认值为10)。 输出是与输入图像相同类型的数组。
Step 4: Iterate to Explore the Restoration
每次迭代产生的图像都会改变。 要调查图像恢复的演变过程,您可以按照以下步骤进行反褶积:执行一组迭代,查看结果,然后从停止的位置恢复迭代。 为此,输入图像必须作为单元阵列的一部分传递。 例如,通过传递{BlurredNoisy}而不是BlurredNoisy作为输入图像参数来启动第一组迭代。
luc1_cell = deconvlucy({BlurredNoisy},PSF,5);
在这种情况下,输出luc1_cell变成单元阵列。 单元输出包含四个数值数组,其中第一个是BlurredNoisy图像,第二个是恢复的类double图像,第三个数组是第一个倒数第一个迭代的结果,第四个数组是内部参数 的迭代集合。 输出单元阵列的第二个数组阵列图像luc1_cell {2}与步骤3的输出阵列(图像luc1)完全相同,可能除了它们的类别(单元格输出始终会给出类别double的恢复映像)。
要恢复迭代,请从前一个函数调用的输出中取出单元阵列luc1_cell,并将其传递给去卷积函数。 使用默认的迭代次数(NUMIT = 10)。 恢复的图像是总共15次迭代的结果。
luc2_cell = deconvlucy(luc1_cell,PSF);
luc2 = im2uint8(luc2_cell{2});
figure;
imshow(luc2);
title('Restored Image, NUMIT = 15');
Step 5: Control Noise Amplification by Damping
最新的图像luc2是15次迭代的结果。 虽然它比5次迭代的早期结果更清晰,但图像呈现出“斑点”外观。 这些斑点不符合任何实际结构(将其与真实图像进行比较),而是将数据中的噪音过于紧密地结合起来。
要控制噪声放大,请通过指定DAMPAR参数来使用阻尼选项。 DAMPAR必须与输入图像具有相同的类别。 该算法在与噪声相比差异较小的区域中抑制了模型中的变化。 这里使用的DAMPAR等于噪声的3个标准偏差。 注意图像更平滑。 DAMPAR = im2uint8(3*sqrt(V));
luc3 = deconvlucy(BlurredNoisy,PSF,15,DAMPAR);
figure;
imshow(luc3);
title('Restored Image with Damping, NUMIT = 15');
本示例的下一部分使用模拟的星形图像(为了简单和快速)探讨了解卷函数的WEIGHT和SUBSMPL输入参数。
Step 6: Create Sample Image
这个例子创建了一个四颗星的黑白图像。I = zeros(32); I(5,5) = 1; I(10,3) = 1; I(27,26) = 1; I(29,25) = 1; figure; imshow(1-I,[],'InitialMagnification','fit'); ax = gca; ax.Visible = 'on'; ax.XTickLabel = []; ax.YTickLabel = []; ax.XTick = [7 24]; ax.XGrid = 'on'; ax.YTick = [5 28]; ax.YGrid = 'on'; title('Data');
Step 7: Simulate a Blur
PSF = fspecial('gaussian',15,3); Blurred = imfilter(I,PSF,'conv','sym');
现在模拟一个只能观察部分恒星图像的相机(只能看到模糊)。 创建一个加权函数数组WEIGHT,其中包含模糊图像中心部分(位于虚线内的“好”像素)和边缘零点(“坏”像素 - 那些不接收信号的像素)。
WT = zeros(32); WT(6:27,8:23) = 1; CutImage = Blurred.*WT;
为了减少与边界相关的振铃,请将边界限制器功能应用于给定的PSF。
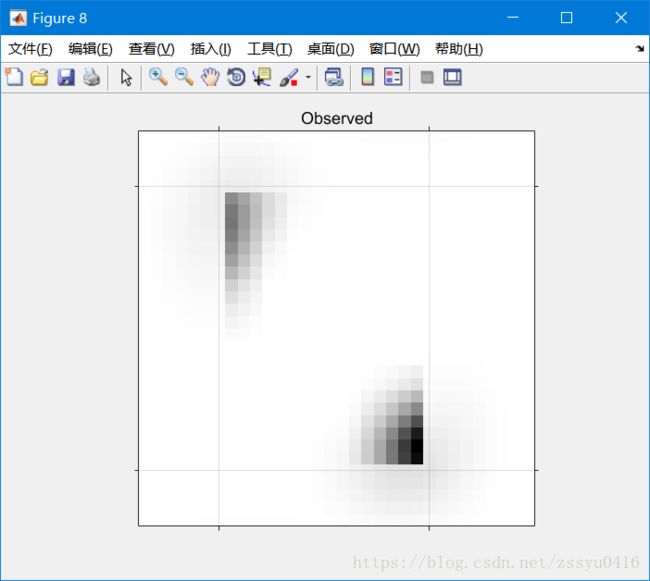
CutEdged = edgetaper(CutImage,PSF); figure; imshow(1-CutEdged,[],'InitialMagnification','fit'); ax = gca; ax.Visible = 'on'; ax.XTickLabel = []; ax.YTickLabel = []; ax.XTick = [7 24]; ax.XGrid = 'on'; ax.YTick = [5 28]; ax.YGrid = 'on'; title('Observed');
Step 8: Provide the WEIGHT Array
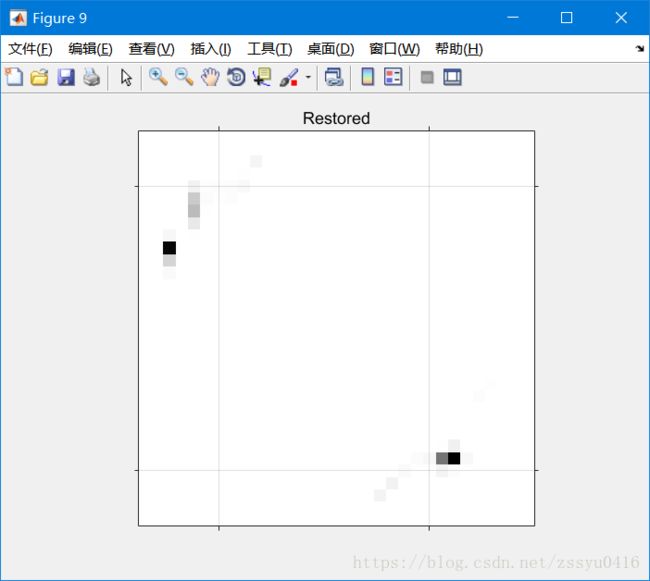
该算法在恢复图像时根据WEIGHT数组对每个像素值进行加权。 在我们的例子中,只使用中心像素的值(WEIGHT = 1),而“坏”像素值从优化中排除。 但是,该算法可以将信号功率置于这些“坏”像素的位置,超出相机视图的边缘。 注意已解决星位置的准确性。
luc4 = deconvlucy(CutEdged,PSF,300,0,WT); figure; imshow(1-luc4,[],'InitialMagnification','fit'); ax = gca; ax.Visible = 'on'; ax.XTickLabel = []; ax.YTickLabel = []; ax.XTick = [7 24]; ax.XGrid = 'on'; ax.YTick = [5 28]; ax.YGrid = 'on'; title('Restored');
Step 9: Provide a finer-sampled PSF
在给定更精细的采样PSF(更细SUBSMPL时间)的情况下,deconvlucy可以恢复欠采样图像。 为了模拟较差解析的图像和PSF,该示例在每个维度中将Blurred图像和原始PSF(一个中的两个像素)分组。
Binned = squeeze(sum(reshape(Blurred,[2 16 2 16]))); BinnedImage = squeeze(sum(Binned,2)); Binned = squeeze(sum(reshape(PSF(1:14,1:14),[2 7 2 7]))); BinnedPSF = squeeze(sum(Binned,2)); figure; imshow(1-BinnedImage,[],'InitialMagnification','fit'); ax = gca; ax.Visible = 'on'; ax.XTick = []; ax.YTick = []; title('Binned Observed');
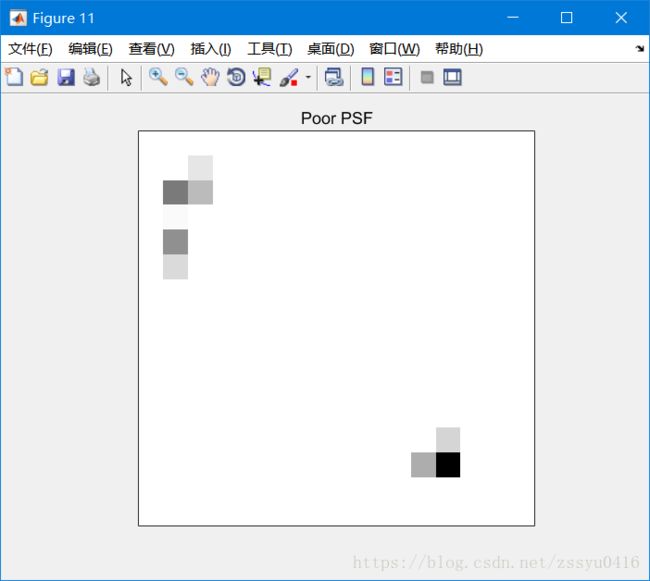
使用欠采样PSF BinnedPSF恢复欠采样图像BinnedImage。 请注意,luc5图像仅区分3颗星。
luc5 = deconvlucy(BinnedImage,BinnedPSF,100); figure; imshow(1-luc5,[],'InitialMagnification','fit'); ax = gca; ax.Visible = 'on'; ax.XTick = []; ax.YTick = []; title('Poor PSF');
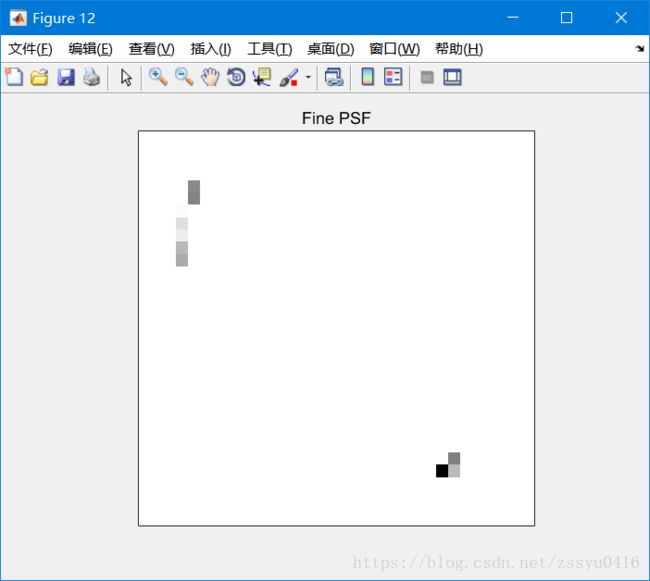
下一个示例恢复欠采样图像(BinnedImage),这次使用更精细的PSF(在SUBSMPL次更精细的网格上定义)。 重建图像(luc6)可以更准确地解析恒星的位置。 请注意它如何在图像右下角的两颗星星之间分配力量。 这提示存在两个明亮的物体,而不是一个,就像在以前的修复中那样。
luc6 = deconvlucy(BinnedImage,PSF,100,[],[],[],2); figure; imshow(1-luc6,[],'InitialMagnification','fit'); ax = gca; ax.Visible = 'on'; ax.XTick = []; ax.YTick = []; title('Fine PSF');