Treap
思想
treap=tree+heap,heap不必多说,这个tree是什么?不用猜了,这是二叉排序树。但是为什么二叉排序树要加上个heap呢?因为二叉排序树太不稳定,我们需要找到一个方法来让二叉排序树尽量平衡一些。treap就是其中的一种方法。由于treap代码简便,所以是二叉平衡树的一种不错的选择。
treap和二叉排序树差不多,但是对于每个节点,除了权值之外,还多了一个优先级。如果看权值,这是一棵二叉排序树,如果看优先级,这是一棵二叉堆(但是并不一定是完全二叉树,所以treap的期望复杂度是log2(n),只是期望,不过实际表现还是不错的)。那么如何维护呢,我们需要通过旋转,在讲旋转之前先来看这个:

由于二叉排序树的特性,我们知道左边都小于右边,那么如果不改变这个特性就不会让这棵树不满足二叉排序树,那么我们就可以旋转一下了。
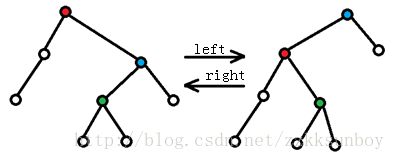
这样的话只是把红蓝绿三点都换了个father,没改变左右顺序,所以依然满足二叉排序树,有了旋转操作我们就可以达到儿子和父亲交换但是却不改变二叉排序树性质的效果了,这个有什么用呢?维护堆(大根或者小根都可以)性质!
当插入一个节点的时候,先把这个节点放到最下面(就和堆一样,放到最下面的同时还需要满足二叉排序树),然后给这个节点一个随机的优先级,如果不满足堆性质就旋转,然后就可以让这棵树即满足堆性质又满足二叉排序树性质了。有了堆性质的加入,treap的期望复杂度就是log2(n)了。
模板
#includereturn 0;if (k==x) return -1;if (k>x) return 1;} //这个函数可以用来确定位置
void Pushup() {si=son[0]->si+son[1]->si+w;}
};
Treap tem[maxn+5],*null=&tem[0],*ro=null; //用人工null代替NULL
Treap* NewTreap(int k,int n)
{
len++;tem[len].w=tem[len].si=n;tem[len].x=k;tem[len].p=rand();
tem[len].son[0]=tem[len].son[1]=null;
return &tem[len];
}
void Rotate(Treap* &id,int d) //旋转
{
Treap* t=id->son[d^1];id->son[d^1]=t->son[d];t->son[d]=id;
id->Pushup();t->Pushup();id=t;
}
void Insert(Treap* &id,int x,int n) //插入
{
if (id==null) {id=NewTreap(x,n);return;}
int d=id->cmp(x);
if (d==-1) id->w+=n; else
{
Insert(id->son[d],x,n);
if (id->son[d]->p>id->p) Rotate(id,d^1); //不满足堆性质,旋转
}
id->Pushup();
}
void Delete(Treap* &id,int x) //删除
{
if (id==null) return;
int d=id->cmp(x);
if (d==-1)
{
if (id->w>1) id->w--; else
if (id->son[0]==null) id=id->son[1]; else
if (id->son[1]==null) id=id->son[0]; else
{
int son;if (id->son[0]->p>id->son[1]->p) son=0; else son=1;
Rotate(id,son^1);if (id==null) return; //防止无效访问
Delete(id->son[son^1],x); //原来的id被旋下去了,继续跟踪原id
}
if (id==null) return; //防止无效访问
} else Delete(id->son[d],x);
id->Pushup();
}
int Kth(Treap* id,int k) //第k大,和普通二叉排序树一样
{
if (id==null) return -1;
if (id->son[0]->siid->son[0]->si+id->w) return id->x; else
if (k<=id->son[0]->si) return Kth(id->son[0],k); else return Kth(id->son[1],k-(id->son[0]->si+id->w));
}
int get_rank(Treap* id,int k) //k的名次,和普通二叉排序树一样
{
if (id==null) return -1;
int d=id->cmp(k);
if (d==-1) return id->son[0]->si+1; else
if (d==0) return get_rank(id->son[0],k); else
return id->son[0]->si+id->w+get_rank(id->son[1],k);
}
int get_num(Treap* id,int k) //k的个数,和普通二叉排序树一样
{
if (id==null) return 0;
int d=id->cmp(k);
if (d==-1) return id->w; else return get_num(id->son[d],k);
}
int get_pre(Treap* id,int k) //k的前继,和普通二叉排序树一样
{
if (id==null) return -1;
int d=id->cmp(k);
if (d==1)
{
int now=id->x,tem=get_pre(id->son[1],k);
if (tem!=-1) return tem; else return now;
} else return get_pre(id->son[0],k);
}
int get_sub(Treap* id,int k) //k的后继,和普通二叉排序树一样
{
if (id==null) return -1;
int d=id->cmp(k);
if (d==0)
{
int now=id->x,tem=get_sub(id->son[0],k);
if (tem!=-1) return tem; else return now;
} else return get_sub(id->son[1],k);
}
void Join(Treap* &A,Treap* B) //把Treap B加入Treap A中
{
if (B==null) return;
Insert(A,B->x,B->w);
Join(A,B->son[0]);Join(A,B->son[1]);
}
bool Eoln(char ch) {return ch==10||ch==13||ch==EOF;}
int readi(int &x) //读入优化
{
int tot=0,f=1;
char ch=getchar();if (ch==EOF) return EOF;
while ('9''0') {if (ch=='-') f=-f;ch=getchar();}
while ('0'<=ch&&ch<='9') tot=tot*10+ch-48,ch=getchar();
x=tot*f;
return Eoln(ch);
}
int main()
{
freopen("Treap.in","r",stdin);
freopen("Treap.out","w",stdout);
readi(te);
while (te--)
{
int td,x;readi(td);readi(x);
switch(td)
{
case 1:Insert(ro,x,1);break;
case 2:Delete(ro,x);break;
case 3:printf("%d\n",get_rank(ro,x));break;
case 4:printf("%d\n",Kth(ro,x));break;
case 5:printf("%d\n",get_pre(ro,x));break;
case 6:printf("%d\n",get_sub(ro,x));break;
case 7:printf("%d\n",get_num(ro,x));break;
}
}
return 0;
}