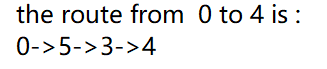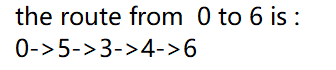图的寻路算法

                             

目录

         图的寻路算法

前言

寻路算法的思路

核心代码详解

测试用例

完整代码获取

博客文章版权声明

---

                                         图的寻路算法

前言

---

前面我们探讨了有关于图的“深度优先遍历”算法，知道了如何利用dfs算法查找图中联通分量的个数，判断图中任意两个节点是否处于同一个联通分量中。其实，深度优先遍历算法能够实现的功能远远不止这些，今天我们就来探讨一下利用深度优先算法如何实现查找图中任意两个节点之间的路径的问题。

 

寻路算法的思路

---

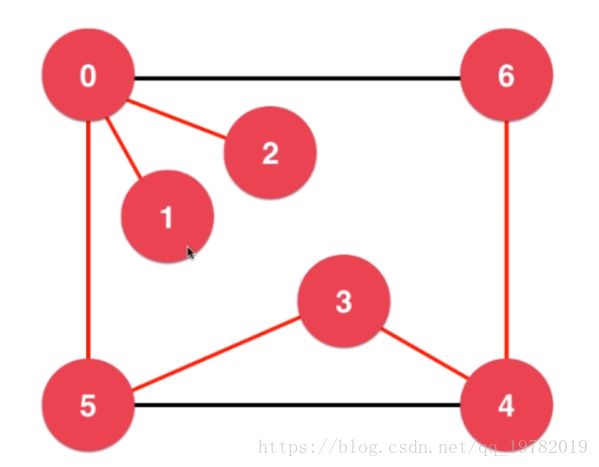
首先，我们还是来看一下上一节中用到的这张图：

我们会发现，其中标记为红颜色的点就表示已经被访问过的点，这些被访问过的节点之间就形成了许多条路径，在遍历的过程中，产生的这些路径如果要是能够记录下来的话，最后我们就能得到一个大的路径表，如若需要查询两点之间的路径情况，则只需要查路径表即可。那么路径表怎么产生的呢？

首先，我们在遍历每一个节点的同时，使用一个整形数组from【】记录下来是从哪一个节点遍历到的这个节点。例如，对于节点1来说，1是从0节点遍历过来的，from[1]=0；对于2也是从0遍历过来from【2】=0；对于5从0遍历过来，from[5]=0;对于3从5遍历过来，对于4从3遍历过来，对于6从4遍历过来。假设我们从0节点开始遍历，就能通过查询路径表从任意一个节点往前一步一步的倒推回0节点，其中经过的节点就组成了路径，但是对于这样的无权图来说，这样生成的路径不一定是最短路径。

 

核心代码详解

---

核心类path的成员参数：

Path类内部拥有一个Graph的引用，一个s代表源节点（起始节点），visited数组用来记录节点是否被访问过，from数组用来记录每个节点上一个遍历的节点是哪个。

private:
    Graph &G;//引用需要进行路径查询的图
    int s;//s为source的意思。即需要寻路的源（起始）节点
    bool* visited;//记录节点是否被访问过
    int * from;//数组用来记录每个节点的上一个节点编号

核心类Path的构造方法：

构造完Path的基本属性后，就开始执行dfs算法，dfs算法会为visited数组和from数组填充有价值的数据。

  Path(Graph &G, int s) : G(G), s(s) {
        assert(s>=0&&s<=G.V());//检查参数，防止越界访问
        visited=new bool[G.V()];//构造visited数组
        from=new int[G.V()];//构造from数组
        //下面是初始化工作
        for (int i = 0; i < G.V(); i++){
            visited[i]=false;
            from[i]=-1;
        }

        //执行dfs算法，把寻路需要使用到的数据准备好
        //即完成visited和from数组的数据准备
        dfs(s);

    }

dfs核心实现代码：

dfs参数一定是未被访问过的点，否则在对其进行dfs就毫无意义了。在每次遍历到新节点后，from就要负责记录新节点是从哪一个节点过来的,即from[新节点]=上一个节点。

 void dfs(int v){//我自己规定dfs算法的传入的参数v必须为未被访问的节点
            visited[v]= true;//设置传入节点visited状态为true
           typename Graph::adjIterator adj(G,v);//提取出图中v节点所有邻边的迭代器
           for (int i = adj.begin(); !adj.end() ; i=adj.next()) {
            if(!visited[i]){
                from[i]=v;//此时访问状态从v节点跳到了与其相邻节点之一的i节点
                dfs(i);//继续对i节点进行深度搜索
            }
           }

       }

寻路算法API设计：

1.判断两点之间是否存在路径，实际上就是判断两点是否在同一个联通分量上，通过一次完整的dfs可以得到一个联通分量，在这里我们只有一个联通分量，所以只要这两个点都被同一次dfs访问过了，则这两个处于同一个联通分量上，那么之间当然存在路径了。

2.产生路径的核心算法Path负责从from表中提取节点的序列号，从终节点的序列号开始一直调用from【终节点】往前推，直到推出某个节点i的from[i]=-1，表示节点i没有前节点，即节点i就是起始源节点。虽然推出来的序列号顺序是反向的路径，但是我们可以把这个反向的节点序列压入一个栈中，然后一个一个出栈放入一个向量vec中保存着，这个向量中保存的序列就是正确的顺序了。

3.showPath主要调用path函数来准备路径数据，并传入一个向量vector给path函数用来存储路径信息。之后再控制输出格式把节点一个一个输出来，就成了一条路径了。

 //判断两点之间是否有路
    bool hasPath(int w){//w为寻路终点
        assert(w>=0&&w &vec){//传入终点w和一个空的向量vec从来存储路径
            assert(w>=0&&w stack1;
            while(w!=-1){
                stack1.push(w);//把s到w的路径逆序压入栈中，再从栈中取出来时就是顺序了
                w=from[w];//起始点s的from[s]一直没被重置过，为初始值-1
            }
            vec.clear();
            while(!stack1.empty()){//从栈中取出路径，此时的路径为顺序
                vec.push_back(stack1.top());//顺序压入向量中
                stack1.pop();
            }


    }


    //显示寻路算法算出来的路径
    void showPath(int w){
                vector vec;
                path(w,vec);//到此时vec从空向量变成了一个存储着路径序列的向量
                //控制输出格式
                cout<<"the route from  "<";
            }
        }

       }

 

测试用例

---

我们构造出一个如下图所示的无向图：

在进行测试：

1.测试从0节点到1节点的路径：

Path dfs(g2,0);
dfs.showPath(1);

结果为：

2.测试从0节点到3节点的路径：

Path dfs(g2,0);
dfs.showPath(3);

结果为：

3.测试从0节点到4节点的路径：

Path dfs(g2,0);
dfs.showPath(4);

结果为：

4.测试从0节点到6节点之间的路径：

Path dfs(g2,0);
dfs.showPath(6);

结果为：

 

完整代码获取

---

如若需要访问完整代码，请点击此处移步GitHub。

 

博客文章版权声明

---

第一条 本博客文章仅代表作者本人的观点，不保证文章等内容的有效性。

第二条 本博客部分内容转载于合作站点或摘录于部分书籍，但都会注明作/译者和原出处。如有不妥之处，敬请指出。

第三条 在征得本博客作者同意的情况下，本博客的作品允许非盈利性引用，并请注明出处：“作者：____转载自____”字样，以尊重作者的劳动成果。版权归原作/译者所有。未经允许，严禁转载。

第四条 对非法转载者，“扬俊的小屋”和作/译者保留采用法律手段追究的权利。

第五条 本博客之声明以及其修改权、更新权及最终解释权均属“扬俊的小屋”。

第六条 以上声明的解释权归“扬俊的小屋”所有。