【飞浆PaddlePaddle-百度架构师手把手带你零基础实践深度学习】day01 -- 基础知识储备
本文基于飞浆PaddlePaddle-百度架构师手把手带你零基础实践深度学习课程,仅供学习交流使用
文章目录
- 1.机器学习和深度学习综述
- 人工智能,机器学习,深度学习之间的关系
- 机器学习
- 机器实现学习的本质
- 深度学习
- 深度学习的历史
- 深度学习发展
- 2.波士顿房价预测模型
- 整体流程
- 数据处理
- 模型设计
- 损失函数
- 训练配置
- 训练过程
- 梯度下降的代码实现
- 随机梯度下降
- 代码实现
- 运行结果
- 3.参考
1.机器学习和深度学习综述
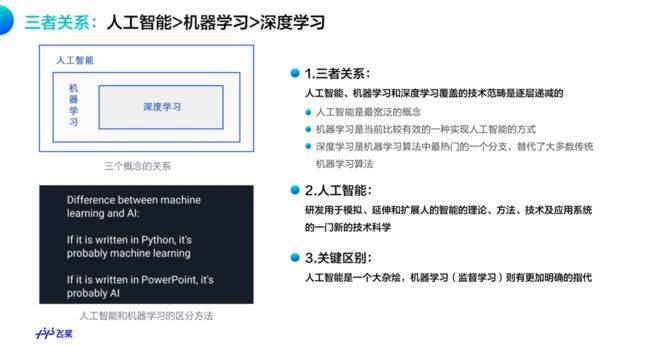
人工智能,机器学习,深度学习之间的关系
机器学习
- 重点讲解模型的三个部分
- 假设
- 评价
- 优化
机器实现学习的本质
机器学习就是拟合一个大的公式,机器学习散构成的三要素如下
- 假设空间:模型的假设或者表示
- 优化目标:评价或者损失函数(loss)
- 寻解算法:优化/求解算法
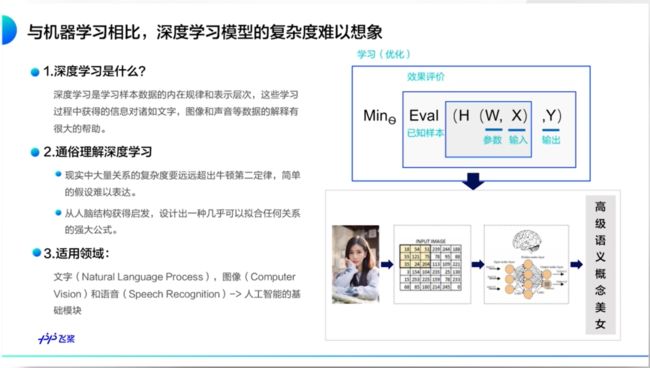
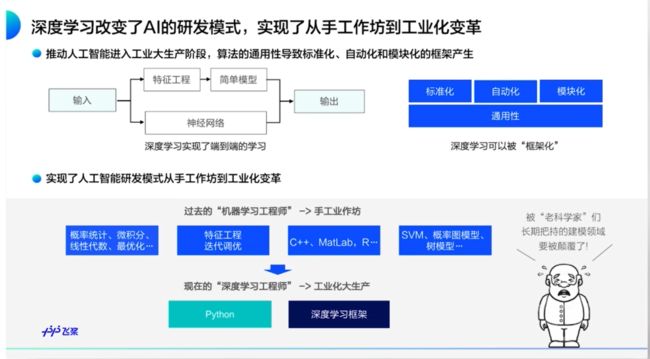
深度学习
深度学习目的是为了设计出可以拟合任何复杂关系的强大公式,最终的目的是为了实现和人脑一样的学习思考
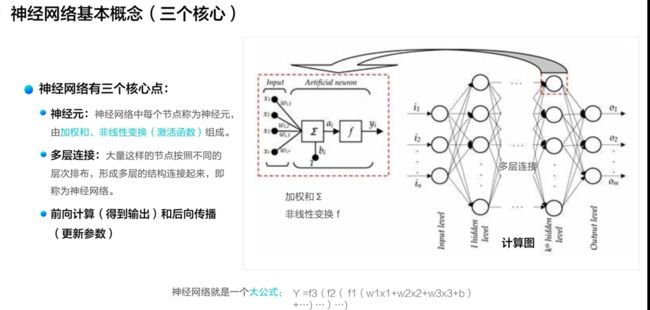
神经网络就是一个大的复杂的公式,并且神经网络的三个核心点
- 神经元
- 多层链接
- 前向计算或者后向传播
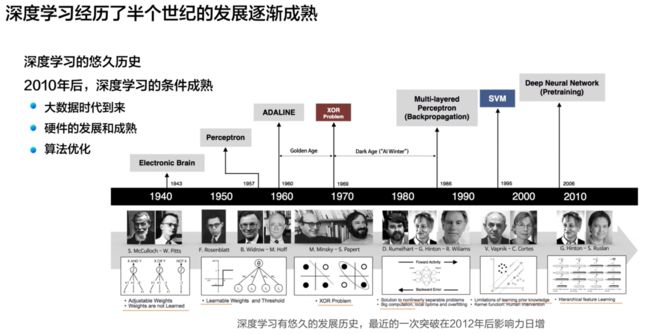
深度学习的历史
时间重点:2010年,深度学习的条件成熟发展,在各行各业有许多切实可行的应用
深度学习发展
重点:
- 深度学习实现了端到端的学习
- 用一个模型进行建模
2.波士顿房价预测模型
整体流程
建立模型的流程
- 数据处理
- 模型设计
- 训练配置
- 训练过程
- 模型保存
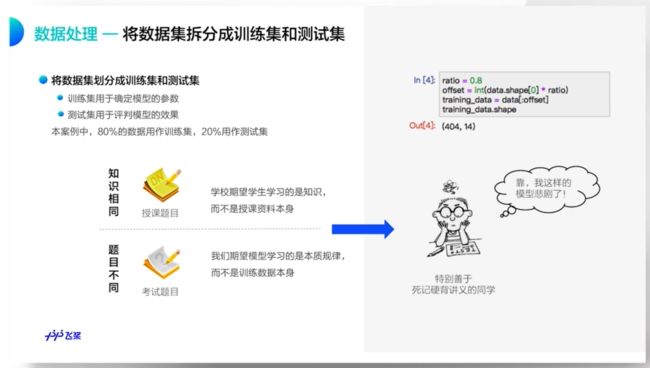
数据处理
归一化的两个好处
- 使得模型训练更加的高效
- 特征前的权重大小可以代表这个变量对预测结果的贡献度
- 样本数数据同样需要归一化处理
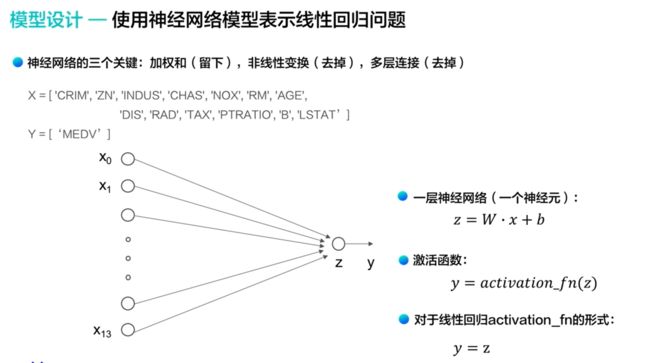
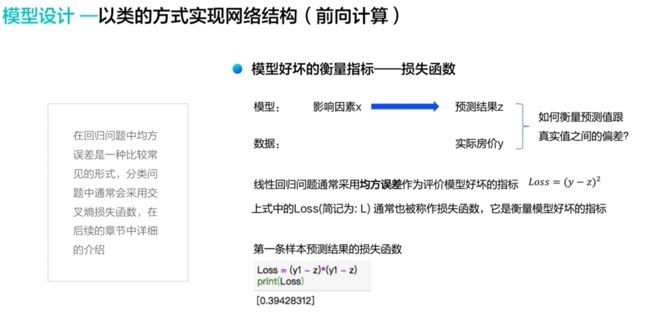
模型设计
神经网络的三个关键
- 加权和留下
- 非线性变化去掉
- 多层连接去掉
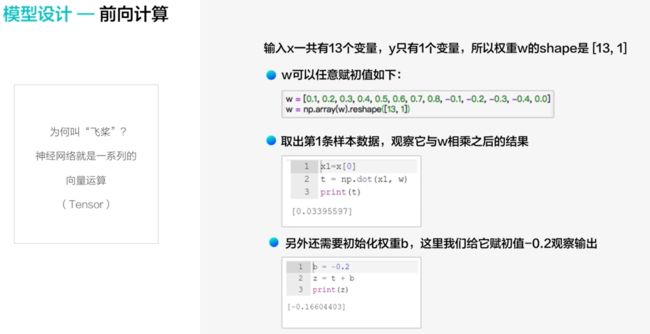
- 重点:神经网络就是一系列向量的运算,这也是为什么叫飞桨的原因
损失函数
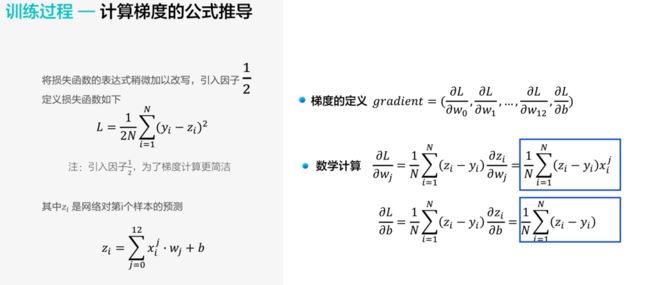
- 损失函数(loss)用以衡量模型好坏的标准的指标 :具体表现为实际与预测结果的差的平方
训练配置
- 多个样本的损失函数,numpy具有广播功能,能实现多样本的计算
两种方法
- 导函数法:求损失函数在极值点出的导数,求解实际的解
- 梯度下降法:求该样本值在对应点的偏导数,类似微积分中对偏导数的定义
训练过程
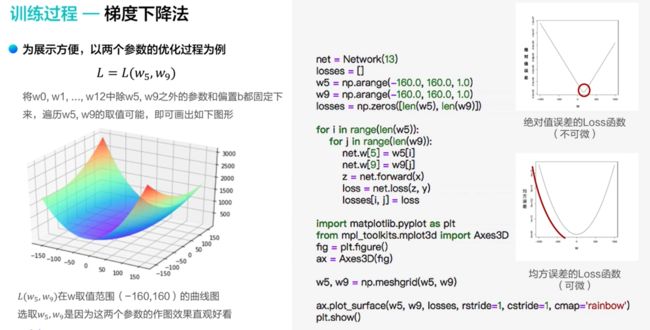
均方误差取平方的原因:
- 所有的点都是可导的
- 有一个最低点(最小的值)
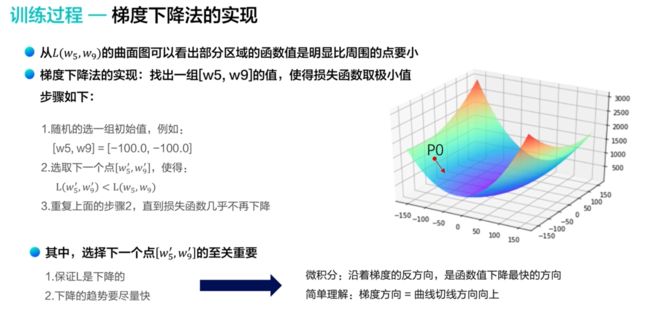
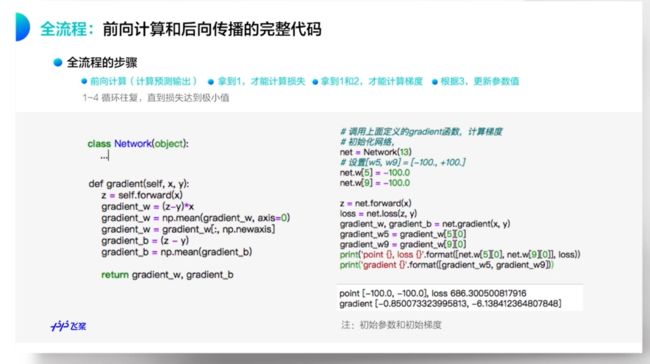
- 在微积分中,梯度的方向是函数增长速度最快的方向,并且是方向导数取得最大值的方向。从而沿着梯度的反方向,是函数值下降的最快的方向
梯度下降的代码实现
- 为了使得统一的步长更加的合适
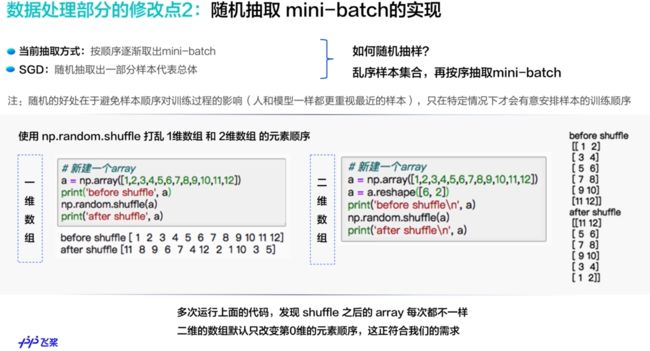
随机梯度下降
- 随机的好处在于避免样本顺序对训练过程的影响,值在特定情况下才会有意安排样本的训练顺序
代码实现
基于随机梯度下降的波士顿房价预测模型的代码实现
import numpy as np
class Network(object):
def __init__(self, num_of_weights):
# 随机产生w的初始值
# 为了保持程序每次运行结果的一致性,此处设置固定的随机数种子
#np.random.seed(0)
self.w = np.random.randn(num_of_weights, 1)
self.b = 0.
def forward(self, x):
z = np.dot(x, self.w) + self.b
return z
def loss(self, z, y):
error = z - y
num_samples = error.shape[0]
cost = error * error
cost = np.sum(cost) / num_samples
return cost
def gradient(self, x, y):
z = self.forward(x)
N = x.shape[0]
gradient_w = 1. / N * np.sum((z-y) * x, axis=0)
gradient_w = gradient_w[:, np.newaxis]
gradient_b = 1. / N * np.sum(z-y)
return gradient_w, gradient_b
def update(self, gradient_w, gradient_b, eta = 0.01):
self.w = self.w - eta * gradient_w
self.b = self.b - eta * gradient_b
def train(self, training_data, num_epoches, batch_size=10, eta=0.01):
n = len(training_data)
losses = []
for epoch_id in range(num_epoches):
# 在每轮迭代开始之前,将训练数据的顺序随机打乱
# 然后再按每次取batch_size条数据的方式取出
np.random.shuffle(training_data)
# 将训练数据进行拆分,每个mini_batch包含batch_size条的数据
mini_batches = [training_data[k:k+batch_size] for k in range(0, n, batch_size)]
for iter_id, mini_batch in enumerate(mini_batches):
#print(self.w.shape)
#print(self.b)
x = mini_batch[:, :-1]
y = mini_batch[:, -1:]
a = self.forward(x)
loss = self.loss(a, y)
gradient_w, gradient_b = self.gradient(x, y)
self.update(gradient_w, gradient_b, eta)
losses.append(loss)
print('Epoch {:3d} / iter {:3d}, loss = {:.4f}'.
format(epoch_id, iter_id, loss))
return losses
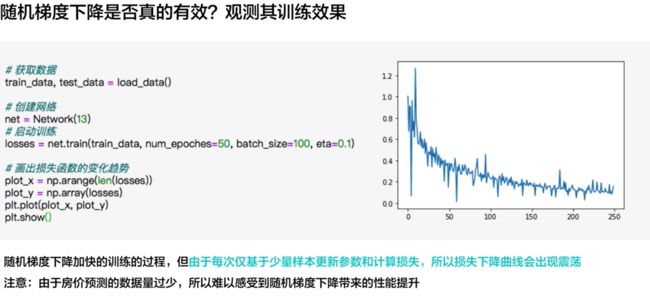
# 获取数据
train_data, test_data = load_data()
# 创建网络
net = Network(13)
# 启动训练
losses = net.train(train_data, num_epoches=50, batch_size=100, eta=0.1)
# 画出损失函数的变化趋势
plot_x = np.arange(len(losses))
plot_y = np.array(losses)
plt.plot(plot_x, plot_y)
plt.show()
- 注:该预测模型中的数据集来自于百度飞桨
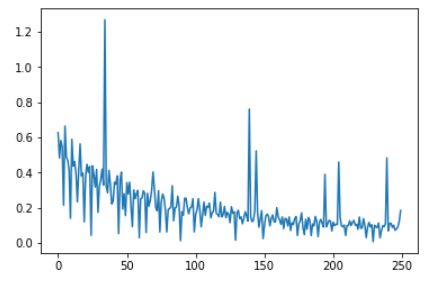
运行结果
Epoch 0 / iter 0, loss = 0.6273
Epoch 0 / iter 1, loss = 0.4835
Epoch 0 / iter 2, loss = 0.5830
Epoch 0 / iter 3, loss = 0.5466
Epoch 0 / iter 4, loss = 0.2147
Epoch 1 / iter 0, loss = 0.6645
Epoch 1 / iter 1, loss = 0.4875
Epoch 1 / iter 2, loss = 0.4707
Epoch 1 / iter 3, loss = 0.4153
Epoch 1 / iter 4, loss = 0.1402
Epoch 2 / iter 0, loss = 0.5897
Epoch 2 / iter 1, loss = 0.4373
Epoch 2 / iter 2, loss = 0.4631
Epoch 2 / iter 3, loss = 0.3960
Epoch 2 / iter 4, loss = 0.2340
Epoch 3 / iter 0, loss = 0.4139
Epoch 3 / iter 1, loss = 0.5635
Epoch 3 / iter 2, loss = 0.3807
Epoch 3 / iter 3, loss = 0.3975
Epoch 3 / iter 4, loss = 0.1207
Epoch 4 / iter 0, loss = 0.3786
Epoch 4 / iter 1, loss = 0.4474
Epoch 4 / iter 2, loss = 0.4019
Epoch 4 / iter 3, loss = 0.4352
Epoch 4 / iter 4, loss = 0.0435
Epoch 5 / iter 0, loss = 0.4387
Epoch 5 / iter 1, loss = 0.3886
Epoch 5 / iter 2, loss = 0.3182
Epoch 5 / iter 3, loss = 0.4189
Epoch 5 / iter 4, loss = 0.1741
Epoch 6 / iter 0, loss = 0.3191
Epoch 6 / iter 1, loss = 0.3601
Epoch 6 / iter 2, loss = 0.4199
Epoch 6 / iter 3, loss = 0.3289
Epoch 6 / iter 4, loss = 1.2691
Epoch 7 / iter 0, loss = 0.3202
Epoch 7 / iter 1, loss = 0.2855
Epoch 7 / iter 2, loss = 0.4129
Epoch 7 / iter 3, loss = 0.3331
Epoch 7 / iter 4, loss = 0.2218
Epoch 8 / iter 0, loss = 0.2368
Epoch 8 / iter 1, loss = 0.3457
Epoch 8 / iter 2, loss = 0.3339
Epoch 8 / iter 3, loss = 0.3812
Epoch 8 / iter 4, loss = 0.0534
Epoch 9 / iter 0, loss = 0.3567
Epoch 9 / iter 1, loss = 0.4033
Epoch 9 / iter 2, loss = 0.1926
Epoch 9 / iter 3, loss = 0.2803
Epoch 9 / iter 4, loss = 0.1557
Epoch 10 / iter 0, loss = 0.3435
Epoch 10 / iter 1, loss = 0.2790
Epoch 10 / iter 2, loss = 0.3456
Epoch 10 / iter 3, loss = 0.2076
Epoch 10 / iter 4, loss = 0.0935
Epoch 11 / iter 0, loss = 0.3024
Epoch 11 / iter 1, loss = 0.2517
Epoch 11 / iter 2, loss = 0.2797
Epoch 11 / iter 3, loss = 0.2989
Epoch 11 / iter 4, loss = 0.0301
Epoch 12 / iter 0, loss = 0.2507
Epoch 12 / iter 1, loss = 0.2563
Epoch 12 / iter 2, loss = 0.2971
Epoch 12 / iter 3, loss = 0.2833
Epoch 12 / iter 4, loss = 0.0597
Epoch 13 / iter 0, loss = 0.2827
Epoch 13 / iter 1, loss = 0.2094
Epoch 13 / iter 2, loss = 0.2417
Epoch 13 / iter 3, loss = 0.2985
Epoch 13 / iter 4, loss = 0.4036
Epoch 14 / iter 0, loss = 0.3085
Epoch 14 / iter 1, loss = 0.2015
Epoch 14 / iter 2, loss = 0.1830
Epoch 14 / iter 3, loss = 0.2978
Epoch 14 / iter 4, loss = 0.0630
Epoch 15 / iter 0, loss = 0.2342
Epoch 15 / iter 1, loss = 0.2780
Epoch 15 / iter 2, loss = 0.2571
Epoch 15 / iter 3, loss = 0.1838
Epoch 15 / iter 4, loss = 0.0627
Epoch 16 / iter 0, loss = 0.1896
Epoch 16 / iter 1, loss = 0.1966
Epoch 16 / iter 2, loss = 0.2018
Epoch 16 / iter 3, loss = 0.3257
Epoch 16 / iter 4, loss = 0.1268
Epoch 17 / iter 0, loss = 0.1990
Epoch 17 / iter 1, loss = 0.2031
Epoch 17 / iter 2, loss = 0.2662
Epoch 17 / iter 3, loss = 0.2128
Epoch 17 / iter 4, loss = 0.0133
Epoch 18 / iter 0, loss = 0.1780
Epoch 18 / iter 1, loss = 0.1575
Epoch 18 / iter 2, loss = 0.2547
Epoch 18 / iter 3, loss = 0.2544
Epoch 18 / iter 4, loss = 0.2007
Epoch 19 / iter 0, loss = 0.1657
Epoch 19 / iter 1, loss = 0.2000
Epoch 19 / iter 2, loss = 0.2045
Epoch 19 / iter 3, loss = 0.2524
Epoch 19 / iter 4, loss = 0.0632
Epoch 20 / iter 0, loss = 0.1629
Epoch 20 / iter 1, loss = 0.1895
Epoch 20 / iter 2, loss = 0.2523
Epoch 20 / iter 3, loss = 0.1896
Epoch 20 / iter 4, loss = 0.0918
Epoch 21 / iter 0, loss = 0.1583
Epoch 21 / iter 1, loss = 0.2322
Epoch 21 / iter 2, loss = 0.1567
Epoch 21 / iter 3, loss = 0.2089
Epoch 21 / iter 4, loss = 0.2035
Epoch 22 / iter 0, loss = 0.2273
Epoch 22 / iter 1, loss = 0.1427
Epoch 22 / iter 2, loss = 0.1712
Epoch 22 / iter 3, loss = 0.1826
Epoch 22 / iter 4, loss = 0.2878
Epoch 23 / iter 0, loss = 0.1685
Epoch 23 / iter 1, loss = 0.1622
Epoch 23 / iter 2, loss = 0.1499
Epoch 23 / iter 3, loss = 0.2329
Epoch 23 / iter 4, loss = 0.1486
Epoch 24 / iter 0, loss = 0.1617
Epoch 24 / iter 1, loss = 0.2083
Epoch 24 / iter 2, loss = 0.1442
Epoch 24 / iter 3, loss = 0.1740
Epoch 24 / iter 4, loss = 0.1641
Epoch 25 / iter 0, loss = 0.1159
Epoch 25 / iter 1, loss = 0.2064
Epoch 25 / iter 2, loss = 0.1690
Epoch 25 / iter 3, loss = 0.1778
Epoch 25 / iter 4, loss = 0.0159
Epoch 26 / iter 0, loss = 0.1730
Epoch 26 / iter 1, loss = 0.1861
Epoch 26 / iter 2, loss = 0.1387
Epoch 26 / iter 3, loss = 0.1486
Epoch 26 / iter 4, loss = 0.1090
Epoch 27 / iter 0, loss = 0.1393
Epoch 27 / iter 1, loss = 0.1775
Epoch 27 / iter 2, loss = 0.1564
Epoch 27 / iter 3, loss = 0.1245
Epoch 27 / iter 4, loss = 0.7611
Epoch 28 / iter 0, loss = 0.1470
Epoch 28 / iter 1, loss = 0.1211
Epoch 28 / iter 2, loss = 0.1285
Epoch 28 / iter 3, loss = 0.1854
Epoch 28 / iter 4, loss = 0.5240
Epoch 29 / iter 0, loss = 0.1740
Epoch 29 / iter 1, loss = 0.0898
Epoch 29 / iter 2, loss = 0.1392
Epoch 29 / iter 3, loss = 0.1842
Epoch 29 / iter 4, loss = 0.0251
Epoch 30 / iter 0, loss = 0.0978
Epoch 30 / iter 1, loss = 0.1529
Epoch 30 / iter 2, loss = 0.1640
Epoch 30 / iter 3, loss = 0.1503
Epoch 30 / iter 4, loss = 0.0975
Epoch 31 / iter 0, loss = 0.1399
Epoch 31 / iter 1, loss = 0.1595
Epoch 31 / iter 2, loss = 0.1209
Epoch 31 / iter 3, loss = 0.1203
Epoch 31 / iter 4, loss = 0.2008
Epoch 32 / iter 0, loss = 0.1501
Epoch 32 / iter 1, loss = 0.1310
Epoch 32 / iter 2, loss = 0.1065
Epoch 32 / iter 3, loss = 0.1489
Epoch 32 / iter 4, loss = 0.0818
Epoch 33 / iter 0, loss = 0.1401
Epoch 33 / iter 1, loss = 0.1367
Epoch 33 / iter 2, loss = 0.0970
Epoch 33 / iter 3, loss = 0.1481
Epoch 33 / iter 4, loss = 0.0711
Epoch 34 / iter 0, loss = 0.1157
Epoch 34 / iter 1, loss = 0.1050
Epoch 34 / iter 2, loss = 0.1378
Epoch 34 / iter 3, loss = 0.1505
Epoch 34 / iter 4, loss = 0.0429
Epoch 35 / iter 0, loss = 0.1096
Epoch 35 / iter 1, loss = 0.1279
Epoch 35 / iter 2, loss = 0.1715
Epoch 35 / iter 3, loss = 0.0888
Epoch 35 / iter 4, loss = 0.0473
Epoch 36 / iter 0, loss = 0.1350
Epoch 36 / iter 1, loss = 0.0781
Epoch 36 / iter 2, loss = 0.1458
Epoch 36 / iter 3, loss = 0.1288
Epoch 36 / iter 4, loss = 0.0421
Epoch 37 / iter 0, loss = 0.1083
Epoch 37 / iter 1, loss = 0.0972
Epoch 37 / iter 2, loss = 0.1513
Epoch 37 / iter 3, loss = 0.1236
Epoch 37 / iter 4, loss = 0.0366
Epoch 38 / iter 0, loss = 0.1204
Epoch 38 / iter 1, loss = 0.1341
Epoch 38 / iter 2, loss = 0.1109
Epoch 38 / iter 3, loss = 0.0905
Epoch 38 / iter 4, loss = 0.3906
Epoch 39 / iter 0, loss = 0.0923
Epoch 39 / iter 1, loss = 0.1094
Epoch 39 / iter 2, loss = 0.1295
Epoch 39 / iter 3, loss = 0.1239
Epoch 39 / iter 4, loss = 0.0684
Epoch 40 / iter 0, loss = 0.1188
Epoch 40 / iter 1, loss = 0.0984
Epoch 40 / iter 2, loss = 0.1067
Epoch 40 / iter 3, loss = 0.1057
Epoch 40 / iter 4, loss = 0.4602
Epoch 41 / iter 0, loss = 0.1478
Epoch 41 / iter 1, loss = 0.0980
Epoch 41 / iter 2, loss = 0.0921
Epoch 41 / iter 3, loss = 0.1020
Epoch 41 / iter 4, loss = 0.0430
Epoch 42 / iter 0, loss = 0.0991
Epoch 42 / iter 1, loss = 0.0994
Epoch 42 / iter 2, loss = 0.1270
Epoch 42 / iter 3, loss = 0.0988
Epoch 42 / iter 4, loss = 0.1176
Epoch 43 / iter 0, loss = 0.1286
Epoch 43 / iter 1, loss = 0.1013
Epoch 43 / iter 2, loss = 0.1066
Epoch 43 / iter 3, loss = 0.0779
Epoch 43 / iter 4, loss = 0.1481
Epoch 44 / iter 0, loss = 0.0840
Epoch 44 / iter 1, loss = 0.0858
Epoch 44 / iter 2, loss = 0.1388
Epoch 44 / iter 3, loss = 0.1000
Epoch 44 / iter 4, loss = 0.0313
Epoch 45 / iter 0, loss = 0.0896
Epoch 45 / iter 1, loss = 0.1173
Epoch 45 / iter 2, loss = 0.0916
Epoch 45 / iter 3, loss = 0.1043
Epoch 45 / iter 4, loss = 0.0074
Epoch 46 / iter 0, loss = 0.1008
Epoch 46 / iter 1, loss = 0.0915
Epoch 46 / iter 2, loss = 0.0877
Epoch 46 / iter 3, loss = 0.1139
Epoch 46 / iter 4, loss = 0.0292
Epoch 47 / iter 0, loss = 0.0679
Epoch 47 / iter 1, loss = 0.0987
Epoch 47 / iter 2, loss = 0.0929
Epoch 47 / iter 3, loss = 0.1098
Epoch 47 / iter 4, loss = 0.4838
Epoch 48 / iter 0, loss = 0.0693
Epoch 48 / iter 1, loss = 0.1095
Epoch 48 / iter 2, loss = 0.1128
Epoch 48 / iter 3, loss = 0.0890
Epoch 48 / iter 4, loss = 0.1008
Epoch 49 / iter 0, loss = 0.0724
Epoch 49 / iter 1, loss = 0.0804
Epoch 49 / iter 2, loss = 0.0919
Epoch 49 / iter 3, loss = 0.1233
Epoch 49 / iter 4, loss = 0.1849
3.参考
- 百度飞桨paddlepaddle