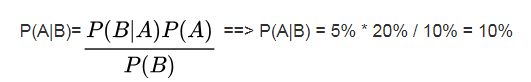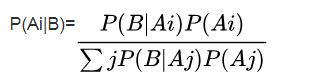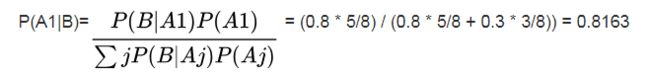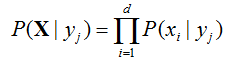机器学习(十一)-Naïve Bayes Classifier朴素贝叶斯分类器及Python实现
原创不易,转载前请注明博主的链接地址:Blessy_Zhu https://blog.csdn.net/weixin_42555080
本次代码的环境:
运行平台: Windows
Python版本: Python3.x
IDE: PyCharm
一、Naïve Bayes Classifier简介
贝叶斯分类器是一类分类算法的总称,贝叶斯定理是这类算法的核心,因此统称为贝叶斯分类(Bayesian Classifier)。贝叶斯决策论通过相关概率已知的情况下利用误判损失来选择最优的类别分类。一提到贝叶斯,一定少不了贝叶斯公式:
贝叶斯分类器的应用背景是:
在很多应用中,属性集和类变量之间的关系是不确定。换句话说,尽管测试记录的属性集和某些训练样例相同。但是也不能确定地预测它的类标号。这种情况产生的原因可能噪声或者出现了某些影响分类的混淆因素却没有包含在分析中。例如,考虑根据一个人的饮食和锻炼的频率来预测他是否有患心脏病的危险。尽管大多数饮食健康、经常锻炼身体的人患心脏病的机率较小,但仍有人由于遗传、过量抽烟、酗酒等其他原因而患病。确定个人的饮食是否健康、体育锻炼是否充分也还是需要论证的课题,这反过来也会给学习问题带来不确定性。贝叶斯分类器,就是这样一种对属性集和类变量的概率关系建模的方法。贝叶斯定理(Bayes theorem),它是一种把类的先验知识和从数据中收集的新证据相结合的统计原理;
本篇博文主要介绍的是朴素贝叶斯分类器(Naïve Bayes Classifier)。
二、Naïve Bayes Classifier理解
2.1 Naïve Bayes公式理解
首先看一个例子,来理解最常见的Naïve Bayes:
一个饭店,所有来吃饭的客人中,会有10%的人喝酒 —— P(B),所有客人中,会有20%的人驾车前来—— P(A),开车来的客人中,会有5%喝酒 —— P(B|A)。那么请问,在这个饭店喝过酒的人里,仍然会开车的比例—— P(A|B)是多少?
接下来,将上面的公式化为更一般的贝叶斯公式:假设事件 A 本身又包含多种可能性,即 A 是一个集合:A={A1,A2,…,An}A={A1,A2,…,An},那么对于集合中任意的 Ai,贝叶斯定理可用下式表示:
接下来再通过一个例子来,理解上面的式子:
某 AI 公司招聘工程师,来了8名应聘者,这8个人里,有5个人是985院校毕业的,另外3人不是。面试官拿出一道算法题准备考察他们。根据以前的面试经验,面试官知道:985毕业生做对这道题的概率是80%,非985毕业生做对率只有30%。现在,面试管从8个人里随手指了一个人——小甲,让 TA 出来做题。结果小甲做对了,那么请问,小甲是985院校毕业的概率是多大?
现在我们来看,这道题里面的小甲的毕业院校有两种可能,也就是 A={A1,A2}
A1 —— 被选中的人是985毕业的;
A2 —— 被选中的人不是985毕业的。
B —— 被选中的人做对了面试题
P(A1) = 5/8
P(A2) = 3/8
P(B|A1) = 80% = 0.8(985毕业生做对该道面试题的先验概率)
P(B|A2) = 30% = 0.3(非985毕业生做对该道面试题的先验概率)
因此:
所以,小甲是985毕业的概率是81.6%
2.2 Naïve Bayes Classifier详细理解
2.2.1 条件独立假设
给定类标号y,朴素贝叶斯分类器在估计类条件概率时假设属性之间条件独立。条件独立假设可形式化地表述为:
其中每个属性集包含d个属性:
2.2.2 Naïve Bayes Classifier工作原理
接下来有了条件独立假设,就不必计算X的每个组合的 类条件概率,只需要对给定的Y,计算每一个Xi的条件概率。后一个方法更实用,因为他不需要很大的训练集就可以获得较好的概率估计。
给定一个未知的数据样本X, 分类法将预测X属于具有最高后验概率的类. 即, 未知的样本分配给类yj, 当且仅当
![]()
根据贝叶斯定理, 有
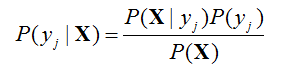
由于P(X) 对于所有类为常数, 只需要最大化P(X|yj)P(yj)即可。
- 估计P(yj)
类yj的先验概率可以用式子估计 P(yj)=nj/n( 其中, nj是类yj中的训练样本数,而n是训练样本总数 ) - 估计P(X|yj)
为便于估计P(X|yj), 假定类条件独立----给定样本的类标号, 假定属性值条件地相互独立.
于是, P(X|Y=yj)可以用下式估计

其中, P(xi |yj)可以由训练样本估值 - 估计P(xi |yj)
设第i个属性Ai是分类属性, 则
P(xi|yj) = nij/nj
其中nij是在属性Ai上具有值xi的yj类的训练样本数, 而nj是yj类的训练样本数
朴素贝叶斯分类器所需要的信息
- 计算每个类的先验概率P(yj)
P(yj)=nj/n
其中, nj是yi类的训练样本数,而n是训练样本总数 - 对于离散属性Ai,设的不同值为ai1, ai2, …,ail ,
对于每个类yj,计算后验概率P(aik|yj), 1<= k <= l
P(aik|yj)= nikj/nj
其中nikj 是在属性Ai上具有值aik 的yj类的训练样本数, 而nj是yj类的训练样本数 - 对于连续属性Ai 和每个类yj,计算yj类样本的均值(Mean)ij,标准差(Standard Deviation)ij
2.2.3 Naïve Bayes Classifier举例
如下表,判断贷款者是否具有拖欠贷款的行为:
如果一个条件概率 P(Xi=xi |Y=yj) 是0, 那么整个表达式的结果也是0
Original: P(Xi=xi |Y=yj) = nij/nj
为了 避免计算概率值为0的问题,可以使用拉普拉斯概率估计(拉普拉斯平滑):
三、Naïve Bayes Classifier的特征以及优缺点
3.1 特征
- 1 面对孤立的噪声点,朴素贝叶斯分类器是健壮的。因为在从数据中估计条件概率时,这些点被平均。通过在建模和分类时忽略样例,朴素贝叶斯分类器也可以处理属性值遗漏问题。
- 2 面对无关属性,该分类器是健壮的。如果Xi是无关属性,那么P(XiIY)几乎变成了均匀分布。Xi的类条件概率不会对总的后验概率的计算产生影响。
- 3 相关属性可能会降低朴素贝叶斯分类器的性能,因为对这些属性,条件独立的假设已不成立。
3.2 优点和缺点 Strengths and Weaknesses
-
朴素贝叶斯分类器与其他方法相比最大的优势或许就在于,它在接受大数据量训练和查询时所具备的高速度。即使选用超大规模的训练集,针对每个项目通常也只会有相对较少的特征数,并且对项目的训练和分类也仅仅是针对特征概率的数学运算而已。
-
尤其当训练量逐渐递增时则更是如此。在不借助任何旧有训练数据的前提下,每一组新的训练数据都有可能会引起概率值的变化。
-
(你会注意到,贝叶斯分类器的算法实现代码允许我们每次只使用一个训练项,而其他方法,比如决策树和支持向量机,则须要我们一次性将整个数据集都传给它们。)对于一个如垃圾邮件过滤这样的应用程序而言,支持增量式训练的能力是非常重要的,因为过滤程序时常要对新到的邮件进行训练,然后必须即刻进行相应的调整;更何况,过滤程序也未必有权访问已经收到的所有邮件信息。
-
朴素贝叶斯分类器的另一大优势是,对分类器实际学习状况的解释还是相对简单的。由于每个特征的概率值都被保存了起来,因此我们可以在任何时候查看数据库,找到最适合的特征来区分垃圾邮件与非垃圾邮件,或是编程语言与蛇。保存在数据库中的这些信息都很有价值,它们有可能会被用于其他的应用程序,或者作为构筑这些应用程序的一个良好基础。
-
朴素贝叶斯分类器的最大缺陷就是,它无法处理基于特征组合所产生的变化结果。假设有如下这样一个场景,我们正在尝试从非垃圾邮件中鉴别出垃圾邮件来:假如我们构建的是一个Web应用程序,因而单词"online"时常会出现在你的工作邮件中。而你的好友则在一家药店工作,并且喜欢给你发一些他碰巧在工作中遇到的奇闻趣事。同时,和大多数不善于严密保护自己邮件地址的人一样,偶尔你也会收到一封包含单词"online pharmacy"的垃圾邮件。
也许你已经看出了此处的难点–我们往往会告诉分类器"online"和"pharmacy"是出现在非垃圾邮件中的,因此这些单词相对于非垃圾邮件的概率会更高一些。当我们告诉分类器有一封包含单词"online pharmacy"的邮件属于垃圾邮件时,则这些单词的概率又会进行相应的调整,这就导致了一个经常性的矛盾。由于特征的概率都是单独给出的,因此分类器对于各种组合的情况一无所知。在文档分类中,这通常不是什么大问题,因为一封包含单词"online pharmacy"的邮件中可能还会有其他特征可以说明它是垃圾邮件,但是在面对其他问题时,理解特征的组合可能是至关重要的。
四、Naïve Bayes Classifier根据姓名判断男女
主要思路:日常从一个人的名字中,基本上能大致判断这个名字的主人是男是女。比如李大志,这个名字一听就很男性。为什么呢?因为大字和志字男性名字用得比较多。虽然机器一眼看不出来,但它可以通过统计信息来判断。如果有足够多的数据,就可以统计出大字和志字用作男性名字的比例,计算概率信息。然后就可以用这些概率,运用上述的贝叶斯公式来进行计算,判定性别。
代码其实不难,各个字的统计数据已经计算好,在数据集中给出。只需要读取文件数据,存储到 python 的字典中,计算出概率,然后预测的时候进行计算即可。
举个栗子,要判断“翟天临”博士是男还是女:
P(gender=男|name=天临)
= P(name=天临|gender=男) * P(gender=男) / P(name=天临)
= P(name has 天|gender=男) * P(name has 临|gender=男) * P(gender=男) / P(name=天临
公式原理为贝叶斯公式,下面对公式中中各个项进行解答:
首先明确我们已经统计得到P(gender=男),P(gender=女)的概率。
怎么算 P(name has 天|gender=男)?
P(name has 天|gender=男)=“天”在男性名字中出现的次数 / 男性字出现的总次数
怎么算 P(gender=男)?
P(gender=男)=男性名出现的次数 / 总次数
怎么算 P(name=天临)?
这个概率对男女来说都是一样的,所以没必要算出来,即我们只需要比较P(name=天临|gender=男) * P(gender=男)和P(name=天临|gender=女) * P(gender=女)两部分谁比较大即可做出判断,并进行选择即可
代码如下(用到的男女姓名数据集在这里。):
#!/usr/bin/env python
# -*- coding: utf-8 -*-
import os
__all__ = ['guess']
def compatNameCharacter(name):
try:
name = name.decode('utf-8')
except:
pass
return name
class Guesser(object):
#step1:init class,一上来,先初始化变量
def __init__(self):
self._load_model()
#待初始化的变量
def _load_model(self):
self.male_total = 0
self.female_total = 0
self.freq = {}
with open(os.path.join(os.path.dirname(__file__),'charfreq.csv'),'rb') as f:
# skip first line第一行是表头,需要跳过
next(f)
for line in f:
line = line.decode('utf-8')
char, male, female = line.split(',')
#完成数据格式转换
char = compatNameCharacter(char)
self.male_total += int(male)
self.female_total += int(female)
self.freq[char] = (int(female), int(male))
self.total = self.male_total + self.female_total
# print(self.total)
# print(self.male_total)
# print(self.female_total)
for char in self.freq:
female, male = self.freq[char]
self.freq[char] = (1. * female / self.female_total,
1. * male / self.male_total)
#print(self.freq) #step1:分析每个字在男女名字的占比
def guess(self, name):
name = compatNameCharacter(name)
#去掉姓,默认是单姓
firstname = name[1:]
for char in firstname:
assert u'\u4e00' <= char <= u'\u9fa0', u'姓名必须为中文'
pf = self.prob_for_gender(firstname, 0)
print('------------')
pm = self.prob_for_gender(firstname, 1)
#step4:最后用男女的对比算的占比推断出性别的概率
if pm > pf:
return ('male', 1. * pm / (pm + pf))
elif pm < pf:
return ('female', 1. * pf / (pm + pf))
else:
return ('unknown', 0)
def prob_for_gender(self, firstname, gender=0):
p = 1. * self.female_total / self.total \
if gender == 0 \
else 1. * self.male_total / self.total
print(p)#step2:p为男女的概率
for char in firstname:
p *= self.freq.get(char, (0, 0))[gender] #step3:每个字在男女总字数里出现的概率
print(char)
print(p)
return p
def guess(name):
guesser = Guesser()
return guesser.guess(name)
if __name__ == '__main__':
print(guess("翟天临"))
输出结果为
天
0.0014011353402999154
临
9.803745729757269e-08
('male', 0.8545506688655845)
所以,叫“天临”的有85.5%的大概率是男同志。
五、总结
朴素贝叶斯分类是一种十分简单的分类算法,叫它朴素贝叶斯分类是因为这种方法的思想真的很朴素。朴素贝叶斯的思想基础是这样的:对于给出的待分类项,求解在此项出现的条件下各个类别出现的概率,哪个最大,就认为此待分类项属于哪个类别。尽管这些特征相互依赖或者有些特征由其他特征决定,然而朴素贝叶斯分类器认为这些属性是独立的(独立性假设)。对于某些类型的概率模型,在监督式学习的样本集中能获取得非常好的分类效果。在许多实际应用中,朴素贝叶斯模型参数估计使用最大似然估计方法;换而言之,在不用到贝叶斯概率或者任何贝叶斯模型的情况下,朴素贝叶斯模型也能奏效。
此分类器的准确率,其实是比较依赖于训练语料的,机器学习算法就和纯洁的小孩一样,取决于其训练条件,如果数据越具有代表性、质量越高,则其训练效果就越好。这篇文章就到这里了,欢迎大佬们多批评指正,也欢迎大家积极评论多多交流。
参考文章
1 贝叶斯分类器 Bayesian Classifier
2 详解贝叶斯分类器
3 根据姓名判断性别-人工智能
4 tf18: 根据姓名判断性别
5 贝叶斯分类算法实例 --根据姓名推测男女