网络中的模块化和社区结构(Modularity and community structure in networks)

作者：M. E. J. Newman
翻译：Wendy

摘要

  人们发现，许多与科学有关的网络，包括社交网络，计算机网络、新陈代谢和监管网络都自然的分为社区或模块。这种社区结构的检测和特征化问题是网络系统研究中的突出问题之一。一种高效的方法是在网络的可能划分范围内优化称为“模块化”的量化函数。在这里，表明可以用网络的特征矩阵的特征向量来表示模块化，我称其为模块化矩阵，并且该表达式导致了一种用于社区检测的光谱算法，该算法比竞争方法在较短的运行时间中返回的结果明显更高的质量。通过将该方法应用到几个已发布的网络数据集来说明该方法的效果。
关键词： 聚类，分区，模块，代谢网络，社交网络

Ⅰ.引言

  很多科学相关的系统都可以将节点集或顶点集通过线或边成对链接表示成网络的形式。例如互联网和万维网，新陈代谢网络，食物网络，神经网络，通信和分发网络以及社交网络。网络系统的研究可以追溯到几个世纪以前，但是在过去的十年中，它受到了特别的关注，特别是在数学科学领域，部分原因是在现实世界中，准确的描述网络拓扑的大规模数据的可用性不断提高。对这些数据的统计分析揭示了一些出乎意料的结构特征，例如网络的可传递性高，幂律分布规律和存在重复的局部图案。

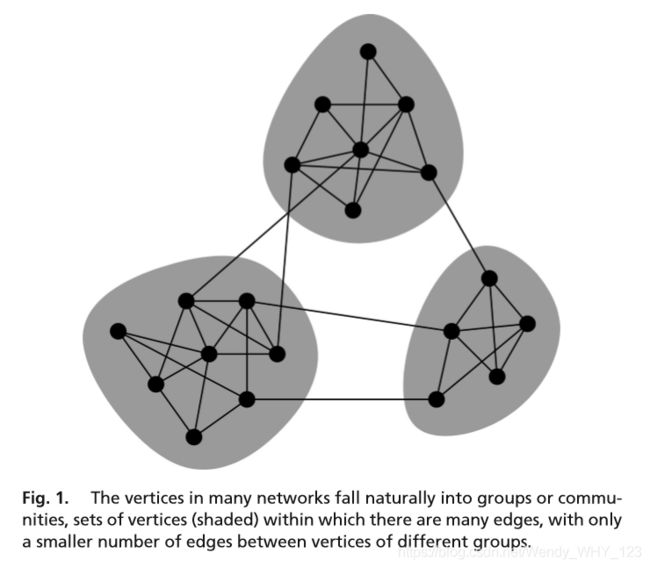
  引起人们注意的一个问题是网络中社区结构的检测和表征，这意味着出现了密集连接的顶点组，而组之间只有稀疏连接（图1）。检测此类群体的能力可能具有重要的实际意义。 例如，万维网中的组可能对应于有关某一个主题的一组网页； 社交网络中的群体可能对应于社交单位或社区。仅仅发现联系紧密的网络就可以传达有用的信息：例如，如果将代谢网络划分为这样的组，则可以为网络动力学的模块化视图提供证据，不同的节点组以不同的程度执行不同的功能 。

  过去有关发现网络中群体的方法主要分为两大研究领域，两者都有悠久的历史。第一个被称为“图形划分”，特别是在计算机科学和相关领域中，并在并行计算和集成电路设计等领域得到了应用。第二种方法是由诸如社会学家，最近由物理学家，生物学家和应用数学家所追求的，以诸如块模型，层次聚类或社区结构检测之类的名称来标识的，尤其是在社会和生物网络中的应用。

  有趣的是，这两条研究路线用了不同的方式却是在解决相同的问题。但是，两个路线的目标之间存在重大差异，因此需要完全不同的技术方法。图分区中的一个典型问题是在并行计算机的处理器之间划分一组任务，以最大程度地减少必要的处理器间通信量。在这种应用中，通常预先知道处理器的数量，并且至少是每个处理器可以处理的任务数量的近似数字。因此，我们知道将网络划分为的组的数量和大小。 同样，目标通常是找到网络的最佳划分，而不管是否存在良好的划分。 在某些情况下，没有什么算法或方法无法划分网络。

  相比之下，最好将社区结构检测视为一种数据分析技术，用于阐明大型网络数据集（如社交网络，互联网和Web数据或生化网络）的结构。社区结构方法通常假定相关的网络自然地分为子组，而实验者的工作是找到这些组。 因此，组的数量和大小由网络本身而不是由实验者确定。而且，社区结构方法可以明确地承认不存在网络的良好划分的可能性，这种结果本身被认为是只对网络拓扑结构发出的相关结果。

  本文重点介绍代表实际系统的网络数据集中的社区结构检测。 但是，社区结构方法和图分区之间的异同将激发随后的许多发展。

Ⅱ.最佳模块化方法（The Method of Optimal Modularity）

  假设然后给定或发现某个网络的结构，并且我们想确定其顶点是否存在自然划分为不重叠的组或社区，其中这些社区的大小可能不限。让我们分阶段解决这个问题，并首先关注网络是否存在任何良好的划分，仅分为两个社区的问题。解决此问题的最明显方法也许是将顶点分为两组，以最大程度地减少各组之间连接的边数。这种“最小切割”方法是图形分割文献中最常采用的方法。但是，如上所述，社区结构问题与图分区有很大不同，因为社区的大小通常不是事先已知的。如果社区大小不受限制，则例如，我们可以自由选择网络的琐碎划分，该划分将所有顶点放入我们的两个组中的一个，而不在另一个中，这保证了组间边缘为零。从某种意义上说，这种划分是最佳的，但是显然它不能告诉我们任何有价值的东西。 如果愿意，我们可以人为地禁止这种解决方案，但是，将一个顶点仅放在一个组中而将其余顶点放在另一个组中的划分通常是最佳的，依此类推。

  问题在于，简单地对边缘进行计数并不是量化社区结构的直观概念的好方法。将网络很好地划分为社区，不仅是在社区之间几乎没有边缘的网络。 社区之间的边缘比预期少。如果两组之间的边缘数量仅是基于随机机会所期望的边缘数量，那么很少有思想的观察者会认为这构成了有意义的社区结构的证据。另一方面，如果组之间的边的数量显着少于我们偶然所期望的数量，或者如果组内的数量明显多于我们所期望的数量，则可以得出结论，有趣的事情正在发生是合理的。

  这个想法，即网络中真正的社区结构对应于统计上令人吃惊的边缘排列，可以通过使用称为模块化的度量来量化。模数最多等于一个乘数常数，即组内的边数减去在随机放置的等价网络中的期望数。 （下面给出了精确的数学公式。）

  模块化可以是正数，也可以是负数，正值表示可能存在社区结构。因此，人们可以通过寻找具有正的，最好是较大的模块化值的网络划分来精确地搜索社区结构。

  因此，有证据表明，这种方法寻找具有高度模块化的社区结构是解决问题的非常有效的方法。例如，Guimera和Amaral以及后来的Danonetal通过模拟退火在计算机生成的测试网络的可能分区上优化了模块化。在使用标准方法进行直接比较时，Danon等人 发现在大多数情况下，此方法优于所有其他用于社区检测的方法，这些方法可识别出您需要注意的地方。根据这些结果，我们认为模块化的最大化可能是当前确定的社区检测方法，同时基于明智的统计原理并且在实践中非常有效。不幸的是，通过模拟退火进行优化对于解决当今科学家面临的大型网络问题不是可行的方法，因为它需要太多的计算工作。已经研究了许多其他的启发式方法，例如贪婪算法和极值优化。在此，我们根据关注网络的频谱特性，根据模块化的重新制定采取了不同的方法。

  假设我们的网络包含n个顶点。当si =1时，表示顶点i在第一个模块组中，当si =-1时，表示顶点i在第二个模块组中。顶点i与j之间的连边用0，1邻接矩阵Aij表示。尽管在有多个边的网络中可以使用更大的值。同时，如果将边随机放置，则顶点i和j之间的边的预期数量为 kikj/2m，其中 ki和kj分别表示节点i和j的度，m=1/2Σiki是网络中所有边的数量。因此模块数量Q由Aij-kikj/2m在属于同一组的所有顶点对i，j上的和给出。如果i和j在同一个组中，则观察到数量1 /2(sisj+1) 为1，否则为0，则可以将模块化表示为

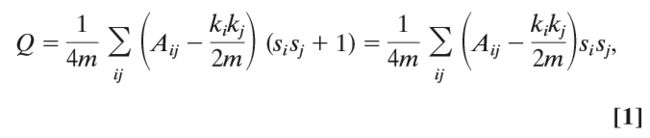
从第二个等式得出2m=Σiki=ΣijAij,1/4m几乎为一常数，包含它是为了与以前的模块化定义兼容，由此等式[1]可以表示成如下的矩阵形式：

其中s是列向量，其元素为si，我们定义了一个具有元素的实对称矩阵B

我们称其为模块化矩阵。我们在本文中的大部分注意力将投入到此矩阵的属性上。目前，请注意，其每一行和每一列的元素总和为零，因此它始终具有特征值零的特征向量（1,1,1，…）。这种观察使人联想到被称为图拉普拉斯的矩阵，该矩阵是最著名的图划分，频谱划分方法之一的基础，并且具有相同的属性。的确，这里介绍的方法与光谱分割有很多相似之处，尽管在某些关键方面也有所不同，我们将看到。

  给定式2所示，我们将s编写为B的归一化特征向量ui的线性组合，从而s=Σ（i=1-n）aiui，其中ai = uiTs。由此我们得到：

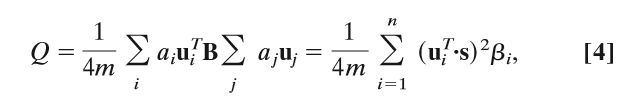
其中βi是对应于特征向量ui的B的特征值。

  让我们假设特征值以降序标记，β1≥β2≥β3···≥βn。我们希望通过选择适当的网络划分或等效地通过选择索引向量s的值来最大化模块化。这意味着选择s以便根据等式中的总和尽可能地集中权重。 等式4涉及最大（最正）特征值。如果对s的选择没有其他限制（除了归一化），这将是一件容易的事：我们只需选择与特征向量u1成比例的s即可。由于特征向量是正交的，因此将所有权重都放在包含最大特征值β1的项中，其他项自动归零。

  不幸的是，对s的元素限制为值±1所施加的问题还有另一个约束，这意味着s通常不能平行于u1选择。但是，让我们尽力而为，使其尽可能接近平行，这等效于最大化点积u1 T·s。很明显，如果将si =+1，则可以达到最大值， u1的对应元素为正，否则si = -1。换句话说，所有对应元素为正的顶点在一组中，其余所有在另一组中。然后，这为我们提供了划分网络的算法：我们计算模块化矩阵的前导特征向量，并根据该向量中元素的符号将顶点分为两组。

  我们立即注意到此方法的一些令人满意的特性。首先，正如已经明确指出的那样，即使没有指定社区的规模，它也可以工作。与使组间边缘的数量最小化的常规分区方法不同，不需要限制组大小或人为地禁止在单个组中具有所有顶点的平凡解决方案。存在对应于这种微分解的本征向量（1,1,1，…），但本征值是零。所有其他本征矢量都与此正交，因此必须同时具有正负元素。因此，只要存在正特征值，此方法就不会将所有顶点都放在同一组中。

  但是，模块化矩阵可能没有正特征值。在这种情况下，前导特征向量是对应于单个组中所有顶点的向量（1,1,1，…）。 但是，这恰好是正确的结果：在这种情况下，该算法告诉我们，没有网络划分会导致积极的模块化，这可以从等式4中立即看出，因为总和中的所有项均为零或负。未分割网络的模块性为零，这是可以实现的最佳状态。这是算法的重要特征。该算法不仅具有有效划分网络的能力，而且在不存在良好划分的情况下也拒绝划分网络。 在后一种情况下，网络将被称为不可分割的。也就是说，如果模块化矩阵没有正特征值，则网络是不可分割的。 这个想法将在以后的发展中发挥关键作用。

  所描述的算法仅利用前导特征向量的元素的符号，但是幅值也传达信息。对应于大量元素的顶点对模块化（等式4）做出了很大贡献，反之则小。或者，如果我们将网络的最佳划分分为两组，然后从一组移动到另一组，则该顶点的向量元素指示模块化将降低多少：不能移动较大量级的元素对应的顶点而不会导致较大的模块化损失，而对应于较小元素的顶点可以以相对较低的成本移动。因此，前导特征向量的元素度量每个顶点属于其分配的社区的牢固程度，带有较大矢量元素的元素是其社区的强中央成员，而带有较小矢量元素的元素则更加矛盾。

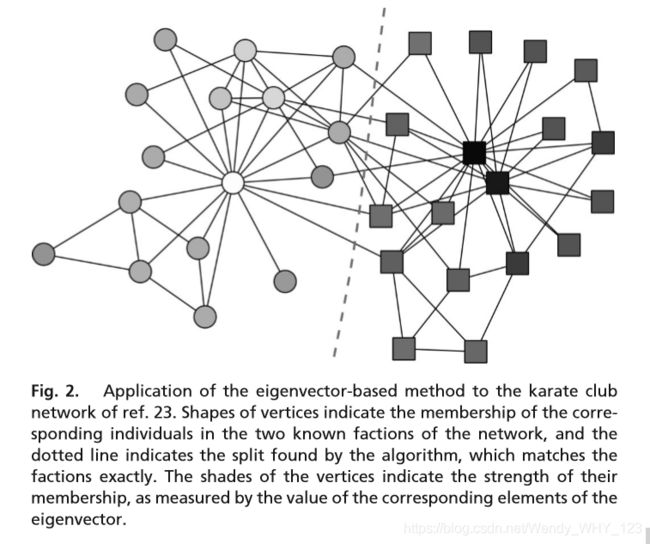
  作为该算法操作的一个示例，图2显示了将其应用到来自社会科学文献的著名网络中的结果，该网络已成为社区检测算法的标准测试。该网络是Zachary的“空手道俱乐部”网络，显示了1970年代一所美国大学的空手道俱乐部成员之间的友谊模式。这个示例特别有趣，因为在观察和构建网络之后不久，由于内部纠纷，相关俱乐部被一分为二。将基于特征向量的算法应用到网络中，我们发现图2中虚线所示的划分与现实生活中俱乐部的已知划分完全吻合，由顶点的形状指示。

  图2中的顶点根据模块化矩阵的主导特征向量中的元素的值进行了阴影处理，并且这些值似乎与俱乐部内已知的社会结构一致。特别是，权重最大的三个顶点（正或负）（图2中的黑色和白色顶点）对应于两个顶点。

Ⅲ.将网络划分为两个以上的社区（Dividing Networks into More than Two Communities）

  在上一节中，介绍了一种简单的基于矩阵的方法，用于将网络很好地分为两部分。但是，许多网络包含两个以上的社区，因此我们希望扩展该方法，以将网络划分为更大的部分。针对此问题的标准方法，此处采用的方法被分为两部分：我们首先使用上一部分的算法将网络分为两部分，然后将这些部分分成四部分。在首先将网络分成两部分后，简单地删除掉两部分之间的边，然后对每个子图应用算法算术，对这一点至关重要。这是因为如果删除边线，则在定义式（1）中出现的度数将发生变化，因此任何随后的模块化度最大化将因此使错误数量最大化。取而代之的是，正确的方法是将大小ng的组g进一步除以2，从而将额外的贡献ΔQ进行模块化。

其中δij是Kronecker δ-符号，使si ^ 2 = 1， B(g)是 ng×ng矩阵，其元素由组g中的顶点的标签i，j索引并具有值

因为等式 5具有与等式2相同的形式，现在，我们可以像以前一样将频谱方法应用于此广义模块化矩阵，以最大化ΔQ。可以观察到B(g)矩阵的行和列项和均为0，如果g组没有被划分，则ΔQ=0。还要注意，对于完整的网络，等式6简化为矩阵形式的等式3之前，因为在这种情况下ΣkBik=0。

  在重复细分网络时，我们需要解决的一个重要问题是在什么时候停止细分过程。该方法的一个很好的功能是它为以下问题提供了明确的答案：如果不存在会增加网络模块化的子图划分，或者等效地为ΔQ提供正值，则没有任何必要再细分，通过将子图相除而获得，应单独放置； 在上一节中，它是不可分割的。当矩阵B（g）没有正特征值时就会发生这种情况，因此前导特征值为细分过程的终止提供了简单的检查：如果前导特征值是零，即它可以取的最小值，那么该子图是不可分割的。

  但是请注意，尽管缺少正特征值是不可分割的充分条件，但这不是必要条件。特别是，如果仅存在小的正特征值和大的负特征值，则等式4中的负βi可能大于正数。 但是，要避免这种可能性是很直接的； 我们只需直接为每个建议的拆分计算模块化贡献ΔQ并确认它大于零。

  因此，算法如下，我们为网络构造模块矩阵等式3，并找到其前导（最正）特征值和相应的特征向量。我们根据该向量的元素的符号将网络分为两部分，然后使用广义模块化矩阵（方程6）对每个部分重复该过程。如果在任何阶段我们发现建议的拆分对总模块性贡献为零或负，则将相应的子图保持未拆分状态。通过这种方式将整个网络分解为不可分割的子图后，该算法结束。

  这种方法的直接推论是，根据定义，网络中的所有“社区”都是不可分割的子图。过去，许多作者提出了关于社区是什么的正式定义。本方法提供了将社区作为不可分割的子图的另一种第一性原则定义。

Ⅳ.模块化最大化的其他技术（Further Techniques for Modularity Maximization）

  在本节中，我将简要介绍通过模块化优化将网络一分为二的另一种方法，这与频谱方法完全不同。尽管其本身并没有特别的意义，但是如稍后将显示的那样，与光谱方法结合使用时，第二种方法非常有效。

  假设我们已将顶点初步分为两组。然后，我们在顶点之间找到一个顶点，当该顶点移到另一组顶点时，将使整个网络的模块增加最大，如果没有增加，则减少最小。我们反复进行这样的移动，但每个顶点只能移动一次。 当所有n个顶点均已移动时，我们在算法运行期间搜索网络所占据的中间状态集，以找到具有最大模块化性的状态。从这种状态再次开始，我们迭代地重复整个过程，直到模块结果没有进一步改善。 那些熟悉图分区文献的人可能会发现该算法让人想起Kernighan-Lin算法，而实际上Kernighan-Lin算法为该方法提供了灵感。

  尽管它很简单，但我们发现这种方法效果不错。它与以前最好的方法没有竞争力，但是在我们已经开发的应用程序中它给出了可指定的模块化值。但是，当该方法与之前介绍的光谱方法结合使用时，它确实可以发挥自己的作用。在标准图分区问题中，通常的方法是使用基于图拉普拉斯图的频谱划分，将网络初步分为两部分，然后使用Kernighan-Lin算法细化该划分。对于社区结构问题，我们发现等效的联合策略非常有效。 基于模块化矩阵前导特征向量的频谱方法很好地指导了社区应该采用的通用形式，然后可以通过顶点移动方法对其进行微调，以达到最佳的模块化值。重复整个过程以细分网络，直到每个剩余的子图都是不可分割的，并且无法进一步提高模块性。 （顺便说一句，我们注意到原则上也可以使用微调方法来完善其他模块化最大化算法的结果，例如参考文献19的极值优化算法。）

  通常，算法的微调阶段只会将模块化的最终值增加几个百分点。 例如，对于图2所示的空手道俱乐部网络，频谱方法本身会发现模块Q = 0.393的网络划分，经微调后可提高到Q = 0.419。 尽管如此，如我们所见，这种幅度的改进是足够的，可以在一种好的方法与一种例外的方法之间进行区分。

Ⅴ.应用范例（ Example Applications ）

  在实践中，开发的算法具有出色的结果。 在此算法与其他算法之间的定量比较中，我们遵循Duch和Arenas（19）的方法，比较了从文献中得出的各种网络的模块化值。表1中显示了六个不同网络的结果，与Duch和Arenas使用的六个网络完全相同。我们将模块化数据与三种先前发布的算法进行比较：Girvan和Newman的基于中间性的算法，该算法已被广泛使用，并已被纳入一些较流行的网络分析程序中； Clauset等人的快速算法，其通过使用贪婪算法来优化模块化； 如果有一种折扣方法不适用于大型网络，例如所有分区的穷举枚举或模拟退火，则可以采用标准方来计算Duch和Arenas的极值优化算法，这是以前最好的方法。

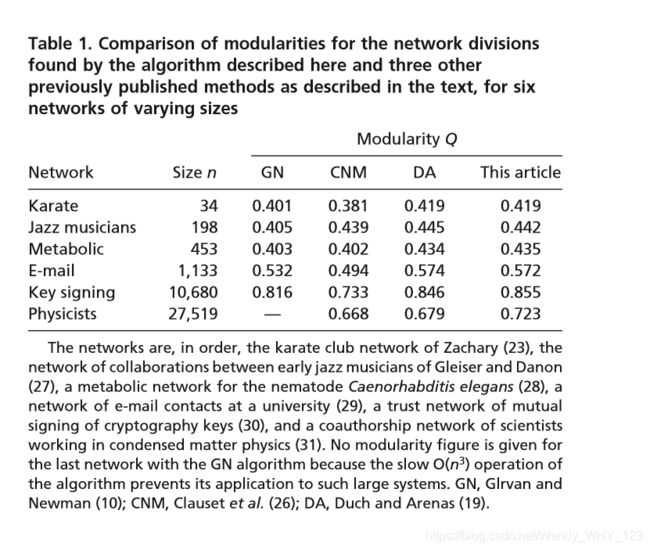
表1揭示了一些有趣的模式。 该算法明，在所有网络中优化模块化的任务中，显优于Girvan和Newman和Clauset等人的方法。 另一方面，极值优化方法更具竞争力。 对于较小的网络，1,000个顶点，本文的方法与极值优化之间基本上没有性能差异； 对于任何给定的网络，这两种算法找到的除法的模块性值相差不超过几千个部分。但是，对于较大的网络，频谱算法的性能优于极值优化，并且随着网络规模的扩大，差距进一步扩大，对于研究的最大网络最大模块化差为6％。因此，对于最近几年特别感兴趣的超大型网络，看来用于检测群落结构的光谱方法可能是此处考虑的最有效的方法。

  表1中给出的模块化值将其应用于实际问题时，可以提供一种有用的定量方法来衡量算法的成功。但是，值得确认的是，它实际上返回了明智的网络划分。我在图2中给出了一个演示这种划分的示例。我还对照先前研究中使用的许多示例网络检查了该方法。 在这里，我再举两个例子，都涉及美国政治的网络代表。

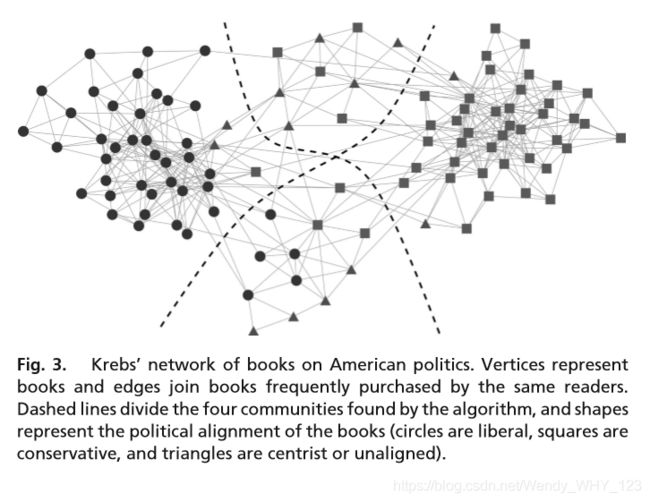
  第一个示例是由V. Krebs（个人交流）编写的有关政治的书籍网络。 在这个网络中，顶点表示从在线书商Amazon.com购买的关于美国政治的105本书，而边合并了同一买家经常购买的成对书籍。根据我明确或明显的政治立场（自由派或保守派）对书籍进行划分（我本人除外），除了少数明确是两党或中间派人士或没有明确隶属关系的书籍。

  图3显示了通过算法馈入该网络的结果。该算法找到四个顶点社区，其模块化度为0.526，在图3中用虚线表示。这些社区中的一个几乎全部是由自由主义书籍组成，而另一个几乎完全由保守主义书籍组成。多数中间专家书都属于其余两个社区。因此，这些书似乎形成了与政治观点紧密契合的共同购买共同体，这一发现鼓励我们相信该算法能够从原始网络数据中提取有意义的结果。尤其值得一提的是，这些中间派书籍属于他们自己的共同体，在大多数情况下并不属于 案件，仅与自由主义者或保守主义者混在一起； 这一发现可能表明政治温和派是他们自己的购买共同体。

  在第二个示例中，我们考虑了一个政治评论网站网络，也称为“博客”或“博客”，由Adamic和Glance从在线目录中编译而成，基于博客的内容，他们还分配了保守派或自由派的政治立场。此处研究的网络的1,225个顶点对应于Adamic 和 Glance网络的最大组成部分中的1,225个博客，并且如果任何一个相应的博客在其首页上都包含指向另一个的超链接，则无向边将顶点连接起来。通过算法将该网络馈入后，我们发现该网络被很好地分为保守社区和自由社区，并且值得注意的是，找到了将Q =0.426分为两个社区的最佳模块化。一个社区有638个顶点，其中620个（97％）代表保守性博客。另一个社区有587个顶点，其中548个（93％）代表自由博客。该算法没有发现这两个组中的任何一个对模块性有积极贡献。 在算法所能确定的范围内，按照此处定义的意义，这些组是“不可分割的”。根据我的经验，这种行为在如此规模的网络中是独一无二的，也许不仅证明了美国当前政治格局的两极分化，而且证明了两个派系的强大凝聚力。

Ⅵ.实操（ Implementation）

  该算法既快速又准确。 该算法最耗时的部分是对模块化矩阵的前导特征向量进行评估。查找此特征向量的最快方法是简单幂方法，即将矩阵重复乘法为试验向量。尽管乍看之下矩阵乘法会很慢，但由于模块矩阵密集，因此每次都要执行O（n2）个运算，但我们可以通过利用矩阵的特定结构来更快地执行它们。令 B = A - kkT/2m，其中A是邻接矩阵，k是向量，其元素为顶点的度数，可以写出B与任意向量x的乘积

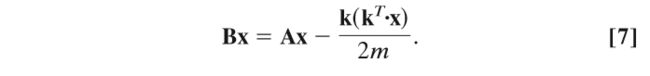
第一项是标准稀疏矩阵乘法，耗时O（m+n），内积kT·x估计耗时O(n) ，因此第二项的总耗时估计为O(n)。因此完成这个多项式的计算需要耗时O（m+n）。通常，对于O [（m + n）n]个整体的运行时间，需要O（n）这样的乘法才能收敛到前导特征向量。通常我们关心的是m正比于n的稀疏图，在这种情况下，运行时间变为O（n2）。扩展此过程以找到广义模块化矩阵公式6的前导特征向量也是一件简单的事情。

  尽管我不会在这里详细介绍，但可以直接显示出算法的微调阶段也可以在O [（m+n）n]时间内完成，因此单个拆分的合并运行时间 图或子图的比例为O [（m+n）n]或稀疏图上的O（n2）。

  然后，我们将划分重复为两部分，直到网络缩小为可分割子图中的分量。整个过程的运行时间取决于这些重复划分形成的树或“树状图”的深度。在最坏的情况下，树状图的深度在n中呈线性，但是只有一小部分可能的树状图实现了这种最坏的情况。通过树状图的平均深度给出更实际的运行时间图，该深度以log n表示，在稀疏情况下，给出了O（n2logn）的整体算法的平均运行时间。这比中间性算法的O（n3）运行快很多，并且比极值优化算法的O（n2log2 n）略好。该算法不如贪婪算法的运行时间O（nlog2 n），但结果的质量比贪婪算法要好得多。实际上，对于使用当前计算机最多可容纳100,000个顶点的网络，运行时间是合理的。对于此处研究的最大网络（协作网络）（拥有27,000个顶点），该算法需要20分钟才能在标准的个人计算机上运行（大约2006年）。

Ⅶ.总结（Conclusions）

  在本文中，我们研究了检测网络中社区结构的问题，该问题被构造为一项优化任务，其中一个任务是在网络的可能划分范围内搜索称为模块化的数量的最大值。我们已经表明，可以根据称为模块化矩阵的矩阵的特征值和特征向量来重写此问题，并且通过利用这种转换，创建了一种用于社区检测的计算机算法，该算法在 结果的质量和执行速度两个方面均表现出了最佳的通用算法。该算法已应用于各种现实世界的网络数据集，包括社会和生物学示例，结果表明，该算法既可以直观地划分出合理的网络划分，也可以给出以模块化程度衡量的数量上更好的划分。