最小生成树\(Prim\)算法
我们通常求最小生成树有两种常见的算法——\(Prim\)和\(Kruskal\)算法,今天先总结最小生成树概念和比较简单的\(Prim\)算法
Part 1:最小生成树基础理论
定义
一个有 \(n\) 个结点的连通图的生成树是原图的极小连通子图,且包含原图中的所有 \(n\) 个结点,并且有保持图连通的最少的边。
——来自百度百科
我们用比较通俗的语言来讲:(百度百科的解释实在是太鬼了,我这个明白人都看着迷糊)
给定一张包含\(n\)个点\(m\)条边的连通带权无向图\(G\),我们从中选出\(n-1\)条边,使得这\(n\)个点互相连通
连通之后,发现所选的\(n-1\)条边和图中的\(n\)个点,构成了一棵树,我们称之为:“生成树”
我们对这棵生成树的所有边权求和,得到一个数\(size\),称之为:“生成树大小”
现在我们就可以字面上理解“最小生成树”是什么意思了——一个图的所有生成树中\(size\)值最小的那一个,就是这个图的最小生成树(\(Minimum\) \(Spanning\) \(Tree\),简称\(MST\))
其实你可以更简单的理解为:最小生成树就是连通\(n\)个点所花费的最小代价
现在我将展示我的画图技巧,举一个例子:
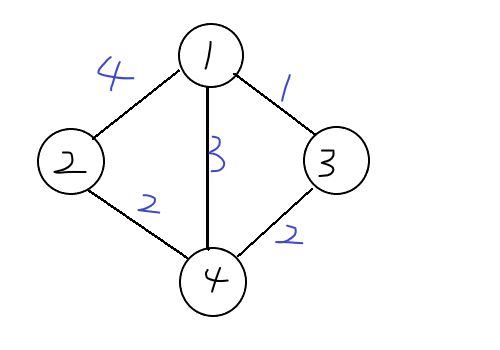
现在给定这张无向图\(G\),我们的任务是求出它的\(MST\)
使用肉眼观察法,我们得到的\(MST\)应该是选择\((1,3),(4,3),(2,4)\)这三条边,权值和为\(5\),也就是我们只花了\(5\)的代价,就把所有点连起来了
通过枚举所有生成树可以发现:不论怎么选,上述方案的权值和一定是最小的,所以它的最小生成树大小为\(5\),包含\((1,3),(4,3),(2,4)\)这三条边
定理
定理:任意一棵最小生成树一定包含无向图中权值最小的边
定理证明:
反证法,假设无向图\(G\)的最小生成树不包含这个权值最小的边(把这个最小权值边设为\(e\)且\(e\)连通点\(x,y\),权值为\(z\))
把\(e\)添加到不包含\(e\)的这棵最小生成树里去,一定会形成一个环,并且环上的每一条\(e\)以外的边的权值一定比\(z\)大
此时,我们随便去掉一条\(e\)以外的边,整个图仍然连通成一棵树,且权值和\(size\)更小(因为加入\(z\),去掉一个大于\(z\)的权)
发现这与一开始的假设矛盾,所以假设不成立,原命题成立,证毕。
Part 2:\(Prim\)算法
\(Prim\)算法原理
这里我们抛开正确性证明,只谈原理(正确性证明是计算机科学家的事,我们需要的是了解与应用)
最初,\(Prim\)算法仅确定\(1\)号节点已经在最小生成树中
\(1、\)设已经选入最小生成树的节点集合为\(T\),没有选入的节点集合为\(S\)
\(2、\)找到一条边\(e(x,y,z)\)(连接\(x,y\),权值为\(z\)),使得\(x\in S,y\in T\)且\(z\)最小
\(3、\)在集合\(S\)中删除\(y\),加入到集合\(T\)中,并累加\(z\)到\(size\)中
\(4、\)重复上述操作,直到集合\(S\)为空为止,此时\(size\)就是最小生成树的大小
具体到代码里可以这么写:
维护一个数组\(dis\),若节点\(i\in S\)则\(dis[i]\)表示节点\(i\)与集合\(T\)中的节点之间权值最小的边的权值,若\(i\in T\)则\(dis[i]\)表示\(i\)被加入\(T\)时选出的最小边的权值
发现这好像与\(dijkstra\)算法要维护的东西有点像:
\(dijkstra\)算法维护一个未知最短路的点到已知最短路的点的最短距离,每次确定到达一个点的最短路,用于更新其他未知点到已知点的最短距离
而\(Prim\)算法维护一个未加入最小生成树的点到已加入最小生成树的点的边权最小值,每次选择一个点加入到最小生成树,更新边权最小值
所以我们可以用一个数组\(vis\)来标记一个节点是否属于集合\(S\),每次从未标记的节点中选出\(dis\)值最小的,把它标记,加入集合\(T\),扫描这个点的所有出边,更新另一个端点的\(dis\)值
最后,当集合\(S\)为空时,算法结束,最小生成树大小为\(\sum_{x=2}^{n}dis[x]\),你也可以直接在选出边权最小值的时候直接累加,不再求和
另外,\(Prim\)算法的时间复杂度为\(O(n^2)\),算不上太优秀,但是因为有求最小值的操作,所以我们可以把\(dis\)数组换成一个小根堆,把时间复杂度优化到\(O(mlogn)\)
\(Code\) \(O(n^2)\)
#include
#include
#define N 5010
using namespace std;
int f[N][N],dis[N],vis[N],m,n,total;
void prim(int x){
memset(dis,0x7f,sizeof(dis));//赋初值无穷大
memset(vis,1,sizeof(vis));//把所有点标记为在集合S中
dis[x]=0;//1号点dis为0
for(int i=1;i<=n;i++){
int k=0;
for(int j=1;j<=n;j++)
if(vis[j]!=0&&(dis[j] 2020/8/15 13:37 update:增加了堆优化\(Prim\)的代码
\(Code\) \(O(mlogn)\)
#include
#include
#include
#include
#include
#include
#include 关于最小生成树\(Prim\)算法的分享就到这里,感谢您的阅读!