行人重识别——评价标准

Rank-n

Query前n个结果中出现正确结果的概率

例如： lable为m1，在100个样本中搜索。

• 如果识别结果是m1、m2、m3、m4、m5、……，则此时rank-1的正确率为100%；rank-2的正确率也为100%；rank-5的正确率也为100%；
• 如果识别结果是m2、m1、m3、m4、m5、……，则此时rank-1的正确率为0%；rank-2的正确率为100%；rank-5的正确率也为100%；
• 如果识别结果是m2、m3、m4、m5、m1、……，则此时rank-1的正确率为0%；rank-2的正确率为0%；rank-5的正确率为100%

---

CMC

CMC，全称Cumulative Matching Characteristics，亦称CMC-k、Rank-k matching accuracy，是目前行人重识别领域最流行的性能评估方法。

考虑一个简单的 single-gallery-shot 情形，每个数据集中的ID（gallery ID）只有一个实例. 对于每一次query, 算法将query图像与gallery中所有图像按照“距离”从小到大排序。CMC top-k accuracy 计算如下：
$$Ac{c}_k=\{\begin{array}{ll}1& iftop-krankedgallerysamplescontainthequeryidentity\\ 0& otherwise\end{array}$$

这是一个平移后的阶跃函数（shifted step function）。CMC曲线的计算方法就是，把每个query的$Ac{c}_k$曲线相加，再除以query的总数，即平均$Ac{c}_k$曲线。典型的CMC曲线如下：

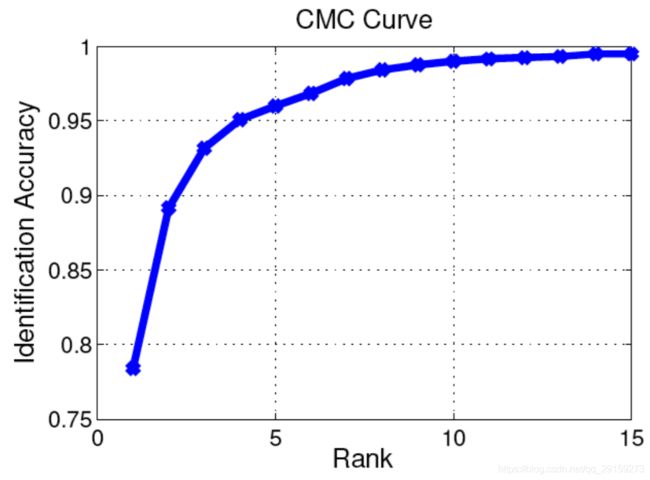
由于$Ac{c}_k$曲线是一个单位阶跃函数，因此CMC曲线必定是一个单调递增的曲线。曲线上某个点如(R5, 0.96)就表示正确结果在前返回所有结果中排名前5的准确率能达到5%。 实际论文中，常取CMC曲线上的某几个点之间对比，比如常出现的Rank1，Rank5，就分别是CMC曲线上，K=1，5时的值。

尽管在 single-gallery-shot 情形下，CMC 有很明确的定义，但是在 multi-gallery-shot 情形下，它的定义并不明确，因为每个gallery identity 可能存在多个instances，所以CMC只适用于“only one ground truth match for a given query”的情况。

CMC曲线显示了待查询行人出现在不同大小的候选列表中的概率。只有在给定查询只有一个真实匹配的情况下(见图3($a$) )，该评估测量才有效。在这种情况下，精确度（Precision）和召回率（Recall）是同样的问题。但是，如果存在多个真实匹配，则 CMC曲线存在偏差，因为未考虑“召回率”。例如，图3($b$) 和图3($c$) 的CMC曲线都等于1，这不能公平地比较两个排序的质量。

---

Precision & Recall

查准率指预测结果中，究竟有多少是真的正？（找出来的对的比例）
$$Precision=\frac{TP}{TP+F}$$

查全率指所有正样本中，究竟预测对了多少个？（找回来了几个）
$$Recall=\frac{TP}{TP+FN}$$

查准率和查全率看上去都很有意义，但我们能直接用它俩来评判ReID模型的性能了吗？当然不行，由于查准率和查全率都是通过比例来计算，完全忽略了返回的结果是有排序的！当查询时，可能返回结果的顺序是一样的，但其查准率和查全率却是一样的。

值得注意的是，查准率和查全率是一个相互矛盾的度量，比如为了增加查全率，我们可以通过增加查询结果的数量来实现，当查询结果数量等于数据集大小时，查全率一定等于1，因为这时所有图片都被查询得到了。但此时查准率就成了最小值。所以比较模型的性能不是那么简单的事情。

那怎么比呢？肉眼比对时，我们常从结果的第一个开始，一个一个比对。借鉴这种思路，我们可以逐渐增加查询结果的数量，从第一个开始，一直到系统给出的查询结果的最后一个，把中间每个点对应的查准率和查全率绘制到图上，得到类似下面的结果：

P-R图直观地显示出了ReID模型的查全率和查准率，显而易见，如果一个模型的P-R曲线包住了另一个模型的P-R曲线，这个模型的性能就好于另一个模型。

显然，PR曲线与坐标轴围起来图形的面积一定程度上反应了ReID模型的性能，我们把这个面积叫做Average Precision。这个面积怎么求？由积分知识可得：

$$AP={\int }_0^{1}p\left(r\right)dr$$

可惜，我们得到的是曲线上一个个点，得不到$p(r)$的准确公式，没法用上面的公式计算。 但是，这个积分可以视作多个长方形条的面积之和，离散化后得到如下公式：

$$AP=\sum _{k=1}^{n}p\left(k\right)\Delta r\left(k\right)$$

其中，$p\left(k\right)$是前k查准率，$\Delta r\left(k\right)=r\left(k\right)-r\left(k-1\right)$。需要注意的是，前k-1个查询结果和前k个查询结果中的同ID结果数量可能一样，所以$\Delta r(k)$可能为0。用公式写出来就是：假设数据集中有$N$个同ID查询结果，则有：

$$\Delta r\left(k\right)=\{\begin{array}{ll}\frac{1}{N}& ID\left(RESUL{T}_k\right)=ID\left(query\right)\\ 0& ID\left(RESUL{T}_k\right)\ne ID\left(query\right)\end{array}$$

---

mAP

mean Average Precision

---

mINP

理想的ReID算法应该使得所有query到的图片排得尽可能靠前，而CMC和mAP都无法体现这一点。

如图7，当CMC相同时，Rank List 1的AP更高，但要更多次查找才能找全正确的匹配。

为了体现这种差异，首先定义negative penalty（NP）：

$$N{P}_i=\frac{R_i^{hard}-\left|G_i\right|}{R_i^{hard}}$$

其中，$R_i^{hard}$指最后一个正确匹配的序号（the rank position of the hardest match）、$\left|G_i\right|$指正确匹配的数量（the total number of correct matches for query $i$）

根据定义，NP越小，算法越好。但是，为了与CMC和mAP保持一致，因此使用inverse negative penalty（INP）。mINP计算式如下：

$$mINP=\frac{1}{n}\sum _i\left(1-N{P}_i\right)=\frac{1}{n}\sum _i\frac{\left|G_i\right|}{R_i^{hard}}$$

---

参考资料

• Open-ReID
• ReID评测标准（rank-n,precision,recall,mAP）
• 深度学习行人重识别ReID最新综述与展望
• 行人重识别(ReID) ——数据集描述 Market-1501
• 《Scalable Person Re-identification: A Benchmark》
• 《Deep Learning for Person Re-identification: A Survey and Outlook》