论文 Copy-and-Paste Networks for Deep Video Inpainting 学习笔记

1. 论文简介

作者本文的目的是对视频进行修复（video inpainting）。简单的视频修复可以理解成在一段拍摄的视频中，有某个运动的物体，我们希望将该物体在视频中删去，同时保持视频的真实自然。本文中作者还将其方法应用在过曝光和欠曝光的场合中，即修复一段视频中过曝光和欠曝光的帧，从而提高道路检测的准确率。

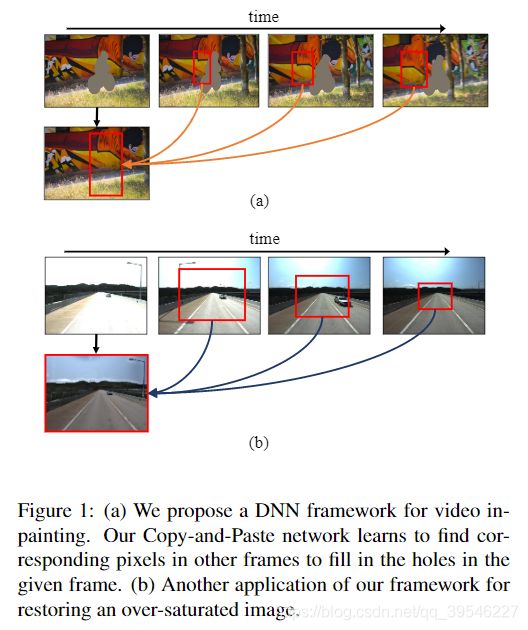
视频修复相比图像修复，需要考虑额外的瞬时信息并保持瞬时一致性（temporally consistent）。我理解的是视频中不同帧之间存在公共的信息，可以借助这些信息来修复帧图像，同时要保证修复后的视频每一帧之间连贯、自然。

作者在文中提出了一种基于 DNN 的框架，叫做复制粘贴网络（Copy-and-Paste Networks）。该网络有两个关键：对齐（alignment）和上下文匹配（context matching）。整个网络的流程可以描述为以下几个步骤：

1. 使用一个自监督的对齐网络（alignment network）将参考帧与目标帧对齐。
2. 在复制网络（copy network）中使用上下文匹配方法复制参考帧中有价值的像素点。
3. 在粘贴网络（paste network）中将复制出来的像素点填补到目标帧的空洞中。
4. 将修复后的目标帧代替原始目标帧添加到视频中，再更新下一个目标帧，重复进行，直到所有帧均被修复。

P.S. 目标帧（target frame）：当前要被填充的帧；参考帧（reference frame）：与目标帧在一定帧数范围内的其他帧。

---

2. 算法实现

网络的整体框架如下图所示，由对齐网络、复制网络、粘贴网络三个部分组成。

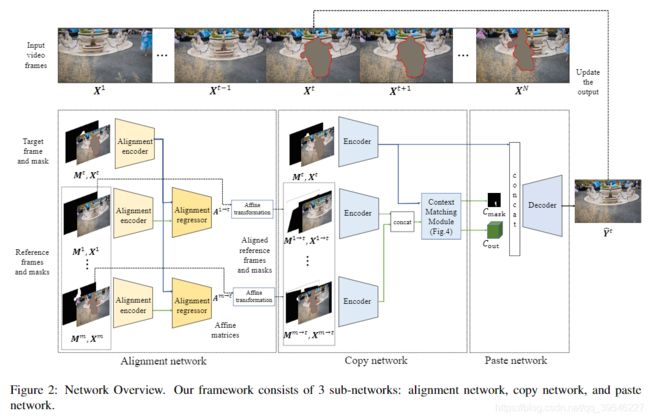
2.1. 对齐网络（Alignment Network）

在视频修复中要填补目标帧中的空洞，往往需要比较大的瞬时窗口（temporal window），即考虑较多的相邻帧，因为对于相隔较远的帧，移动的物体有更大可能性脱离之前目标帧的空洞区域，那么就可以利用这些帧中的信息来对目标帧进行修复，下图可以形象地说明这点：

从图中可以看到，相隔较远的帧重叠区域也较少，能够获得更有价值的信息。

对齐网络结构包含对齐编码器（alignment encoders）和对齐回归器（alignment regressors），具体的细节见补充材料（目前没查到）。

训练对齐网络所用到的损失计算公式如下：
$${\mathcal{L}}_{align}=\sum _r\Vert \mathbf{V}\odot ({\mathbf{X}}^t-{\mathbf{X}}^{r\to t}){\Vert }_1$$

其中 $\mathbf{V}={\mathbf{V}}^t\odot {\mathbf{V}}^{r\to t}$ 是可视图（visibility map），$\odot$ 是点乘符号，$t$ 是目标帧标号，$r$ 是参考帧标号，在可视图中 0 代表空洞像素，1 代表非空洞像素。

注意：对齐网络与后面的网络结构是结合在一起的，采用端到端（end to end）方式，并非独立存在。
 

2.2. 复制粘贴网络（Copy-and-Paste Network）

复制粘贴网络中主要由三个部分组成：编码器，上下文匹配，解码器。

2.2.1. 编码器（Encoder）

编码器用于从目标帧以及对齐后的参考帧中提取特征，其输入为 RGB 图像以及对应的二值 mask，具体的细节见补充材料。

2.2.2. 上下文匹配（Context matching module）

上下文匹配的方法见下图：

参考帧与目标帧之间的全局相似性 ${\theta }^{r,t}$ 计算公式如下：
$${\theta }^{r,t}=\frac{1}{{\sum }_{(x,y)}\mathbf{V}(x,y)}\cdot \sum _{(x,y)}\mathbf{V}(x,y)\cdot {\mathbf{F}}^t(x,y)\cdot {\mathbf{F}}^{r\to t}(x,y)$$

上式其实计算的就是两张特征图之间不包括空洞的余弦相似性。

每个参考帧的显著性图（saliency map，翻译可能不准确）${\mathbf{C}}_{match}^r$ 计算公式如下：
$${\mathbf{S}}^{r,t}={\theta }^{r,t}\cdot {\mathbf{V}}^{r\to t}$$

$${\mathbf{C}}_{match}^r(x,y)=\{\begin{array}{ll}\frac{exp({\mathbf{S}}^{r,t}(x,y))}{{\sum }_{r}exp({\mathbf{S}}^{r,t}(x,y))}& \text{if }{\mathbf{V}}^{r\to t}(x,y)=1\\ 0& otherwise\end{array}$$

下图是一个一维情况的例子。

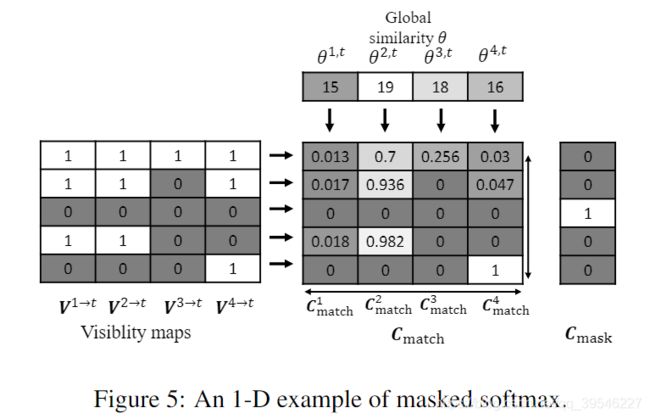
可视图（Visibility maps）每行经过归一化得到最终的显著性图（${\mathbf{C}}_{match}$）（不包括全为空洞的点，下同），对应到二维图像中就是每个点对应的所有参考帧权重相加为 1 ，如下图所示。

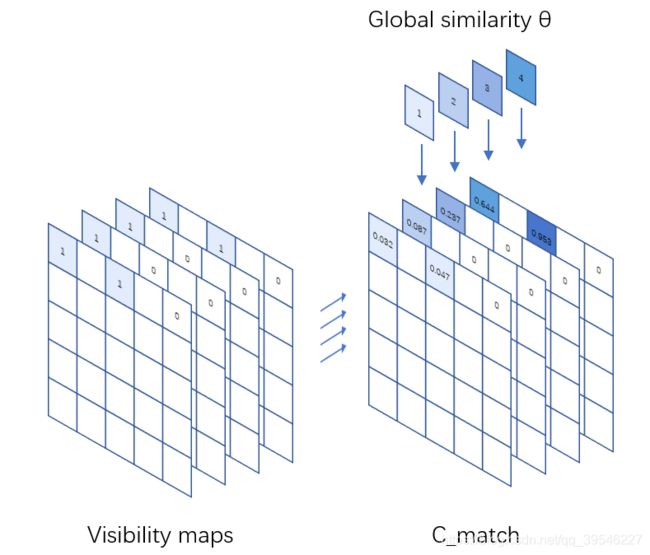
把参考帧的空洞标记也集合起来，用 ${\mathbf{C}}_{mask}$ 来表示，公式为：
$${\mathbf{C}}_{mask}(x,y)=1-(\sum _r{\mathbf{C}}_{match}^r(x,y))$$

通过图 Figure 5 也可以看出，对于所有参考帧中均为空洞的像素点，用 1 表示，否则用 0 表示。

2.2.3. 解码器（Decoder）

解码器网络的输入为目标帧的特征图、${\mathbf{C}}_{out}$ 以及 ${\mathbf{C}}_{mask}$，解码器能够通过合成的参考帧特征以及可视性来填补目标帧中的空洞。作者使用了空洞卷积（dilated convolution）来增大感知野，并设计了更深的网络，通过其他像素点来填补 ${\mathbf{C}}_{mask}=1$ 的空洞。
 

2.3. 瞬时一致性（Temporal Consistency）

算法在对视频进行修复时，每次修复后的目标帧会更新后重新添加到视频中，这么做的目的是为了提高瞬时一致性，在模型简化测试（ablation study）中作者也分析了这么做带了的好处。为了进一步提高瞬时一致性，作者还将网络运行了两次，一次从第一帧到最后一帧，一次从最后一帧到第一帧，最终结果计算如下：
$${\hat{\mathbf{Y}}}_{final}^t={\hat{\mathbf{Y}}}_{forward}^t\cdot \frac{t}{N}+{\hat{\mathbf{Y}}}_{reverse}^t\cdot \frac{(N-t)}{N}$$

---

3. 训练过程

3.1. 损失函数

由于整个网络是端到端的，最终的损失函数包含多个方面。

目标帧中为空洞，其他参考帧中能看到有效像素的区域：
$${\mathcal{L}}_{hole(visible)}=\sum _t^N{\mathbf{M}}^t\odot {\mathbf{C}}_{mask}\odot \Vert {\hat{\mathbf{Y}}}^t-{\mathbf{Y}}^t{\Vert }_1$$

目标帧中为空洞，其他参考帧中也为空洞的区域：
$${\mathcal{L}}_{hole(invisible)}=\sum _t^N{\mathbf{M}}^t\odot (1.-{\mathbf{C}}_{mask})\odot \Vert {\hat{\mathbf{Y}}}^t-{\mathbf{Y}}^t{\Vert }_1$$

目标帧中非空洞区域：
$${\mathcal{L}}_{non-hole}=\sum _t^N(1-{\mathbf{M}}^t)\odot \Vert {\hat{\mathbf{Y}}}^t-{\mathbf{Y}}^t{\Vert }_1$$

为了进一步提高最终结果的视觉效果，作者还加入了 perceptual，style，total variation loss（这里不做翻译）。
$${\mathcal{L}}_{perceptual}=\frac{1}{P}\cdot \sum _p^P\Vert {\varphi }_p({\hat{\mathbf{Y}}}_{comp})-{\varphi }_p(\mathbf{Y}){\Vert }_1$$

$${\mathcal{L}}_{style}=\frac{1}{P}\cdot \sum _p^P\Vert G_p^{\varphi }({\hat{\mathbf{Y}}}_{comp})-G_p^{\varphi }(\mathbf{Y}){\Vert }_1$$

${\mathcal{L}}_{tv}$ 具体表示形式文章未写，使用的目的是减小西洋跳棋效应（checkerboard effect）。

${\hat{\mathbf{Y}}}_{comp}$ 是 ${\hat{\mathbf{Y}}}^t$ 在空洞的区域与 ${\mathbf{X}}^t$ 的非空洞区域的组合，$\varphi$ 是在 ImageNet 上预训练的 VGG-16 网络的池化层输出，$p$ 是池化层的标号，$G$ 是 Gram 矩阵。

总的损失函数为：
$$\begin{array}{rl}\mathcal{L}& =2\cdot {\mathcal{L}}_{align}+10\cdot {\mathcal{L}}_{hole(visible)}+20\cdot {\mathcal{L}}_{hole(invisible)}\\ & +6\cdot {\mathcal{L}}_{non-hole}+0.01\cdot {\mathcal{L}}_{perceptual}+24\cdot {\mathcal{L}}_{style}+0.1\cdot {\mathcal{L}}_{tv}\end{array}$$

各个损失函数的权重分配是由经验确定的（empirically determined）。
 

3.2. 数据库

当前并没有一个图像修复的公共数据集，因此作者使用背景图片以及分割的 masks 合成了一个数据集。合成例子如下图所示。

为了合成背景图像序列，作者采用 Places 单张图片的数据集，对单张图片进行随机裁剪以及一些连续的随机变换（如 shear，scale，translation，rotation）得到最终图像序列。另外作者还使用了另一种方法爬取 Youtube 视频片段，并根据场景划分，从裁剪的视频中随机采样构成图像序列。

为了模拟空洞 masks，作者使用了 MIT Saliency Benchmark 及 Pascal VOC2012 数据集中的目标 masks。先将一个 mask 随机调整到小于背景图片大小的尺寸，然后通过一系列随机变换构成 mask 序列，模拟运动的物体。

将合成的背景图像序列以及模拟的空洞 masks 组合起来就形成了一个 training sample。
 

3.3. 训练细节

作者模型是在 Inter® Core™ i7-7800X CPU(3.5GHz) CPU 以及 NVIDIA TITAN XP GPUs 上跑的。训练时随机选择了 5 个 256 * 256 大小的合成视频作为网络输入，网络设置的 batch size 为 40，使用 Adam 优化器，学习率设置为 $10^{-4}$ 并且每 1 million 次迭代就将学习率降低 10% 。整个训练过程在 3 个 NVIDIA TITAN XP GPUs 上跑了 7 天才完成。

---

4. 测试结果

作者方法在 Amazon Mechanical Turk（AMT）上的测试结果比 VINet 方法效果好，比 Huang 等人提出的方法略差，但速度要快很多。下图展示了部分测试结果。

---

5. 应用

作者将该方法应用在道路监测的恢复过曝光和欠曝光的视频中，效果非常好。


从表中可以看到道路检测的准确率获得了明显的提高。

---

6. 模型简化测试（Ablation Study）

6.1. Masked softmax

作者对比了使用普通 softmax 以及 masked softmax 的结果，如下图所示。

从图可以看出使用 masked softmax 效果更好。
 

6.2. Reference update

作者对比了每次填补完目标帧的空洞后更新与不更新原视频的结果，如下图所示。

从图中可以看到每次更新的结果，其瞬时一致性更好。