机器学习—K均值聚类

0 前言

  主要讲解K均值聚类的算法原理，以及介绍如何利用Python实现具体的算法，其中包括：

1. 介绍K均值聚类的算法原理，使用sklearn实现算法；
2. 利用轮廓系数(Silhouette Coefficient)控制聚类簇数K；
3. 绘制轮廓系数随K波动的折线图，绘图分类后的散点。

 系统及配置 :

1. 系统： win7 x64
2. Python版本： 3.6.4
3. 主要第三方库： scikit-learn 0.21.2 \\ matplotlib 3.1.0 \\

1 K均值聚类

1.1 简介

 k均值聚类算法（k-means clustering algorithm）是一种迭代求解的聚类分析算法，其步骤是随机选取K个对象作为初始的聚类中心，然后计算每个对象与各个种子聚类中心之间的距离，把每个对象分配给距离它最近的聚类中心。聚类中心以及分配给它们的对象就代表一个聚类。每分配一个样本，聚类的聚类中心会根据聚类中现有的对象被重新计算。这个过程将不断重复直到满足某个终止条件。终止条件可以是没有（或最小数目）对象被重新分配给不同的聚类，没有（或最小数目）聚类中心再发生变化，误差平方和局部最小。

                   
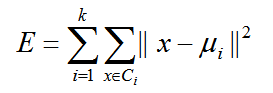
 它的原理是：对于给定的聚类数目k，首先随机创建一个初始分类，然后采用迭代方法通过聚类中心的不断移动来尝试着改进划分。

1.2 实现

# coding: utf-8
"""
    测试k-means算法：
        1. 做一些数据
        2. 聚类
        3. 可视化
"""
import matplotlib.pyplot as plt
from sklearn.datasets.samples_generator import make_blobs
from sklearn.cluster import KMeans

# pre-data
x, y = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=0)  # x, y必须要有固定的格式
print(type(x))
# fit
kmeans = KMeans(n_clusters=4)
kmeans.fit(x)
y_kmeans = kmeans.predict(x)
# plt
plt.scatter(x[:, 0], x[:, 1], c=y_kmeans, cmap='viridis')
centers = kmeans.cluster_centers_
plt.scatter(centers[:, 0], centers[:, 1], c='k', s=200, alpha=0.5)
plt.show()

2 轮廓系数

2.1 简介

 轮廓系数（Silhouette Coefficient），是聚类效果好坏的一种评价方式。最早由 Peter J. Rousseeuw 在 1986 提出。它结合内聚度和分离度两种因素。可以用来在相同原始数据的基础上用来评价不同算法、或者算法不同运行方式对聚类结果所产生的影响。

                   
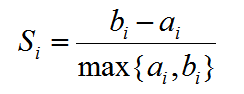
 平均轮廓系数的取值范围为[-1,1]，且簇内样本的距离越近，簇间样本距离越远，平均轮廓系数越大，聚类效果越好。

2.2 实现

# 生成数据模块
from sklearn.datasets import make_blobs
# k-means模块
from sklearn.cluster import KMeans
# 评估指标——轮廓系数,前者为所有点的平均轮廓系数，后者返回每个点的轮廓系数
from sklearn.metrics import silhouette_score, silhouette_samples

import numpy as np
import matplotlib.pyplot as plt

# 生成数据
x_true, y_true = make_blobs(n_samples=600, n_features= 2, centers = 5, random_state= 1)

# 绘制出所生成的数据
plt.figure(figsize= (6, 6))
plt.scatter(x_true[:, 0], x_true[:, 1], c= y_true, s= 10)
plt.title("Origin data")
plt.show()

# 根据不同的n_centers进行聚类
n_clusters = [x for x in range(3, 6)]

for i in range(len(n_clusters)):
    # 实例化k-means分类器
    clf = KMeans(n_clusters=n_clusters[i])
    y_predict = clf.fit_predict(x_true)

    # 绘制分类结果
    plt.figure(figsize=(6, 6))
    plt.scatter(x_true[:, 0], x_true[:, 1], c=y_predict, s=10)
    plt.title("n_clusters= {}".format(n_clusters[i]))

    ex = 0.5
    step = 0.01
    a = np.arange(x_true[:, 0].min() - ex, x_true[:, 0].max() + ex, step)
    xx, yy = np.meshgrid(np.arange(x_true[:, 0].min() - ex, x_true[:, 0].max() + ex, step),
                         np.arange(x_true[:, 1].min() - ex, x_true[:, 1].max() + ex, step))
    print(len(a))
    zz = clf.predict(np.c_[xx.ravel(), yy.ravel()])
    zz.shape = xx.shape

    plt.contourf(xx, yy, zz, alpha=0.1)

    plt.show()

    # 打印平均轮廓系数
    s = silhouette_score(x_true, y_predict)
    print("When cluster= {}\nThe silhouette_score= {}".format(n_clusters[i], s))

    # 利用silhouette_samples计算轮廓系数为正的点的个数
    n_s_bigger_than_zero = (silhouette_samples(x_true, y_predict) > 0).sum()
    print("{}/{}\n".format(n_s_bigger_than_zero, x_true.shape[0]))