2.Matplotlib绘制简单图像
文章目录
- Matplotlib绘制简单图像
- 线图
- 散点图
- plt.plot绘制散点图
- plt.scatter绘制散点图
- 基本误差线
- 密度图与等高线图
- plt.contour()绘制等高线图
- plt.contourf()绘制密度图
- plt.imshow()渲染渐变图像
- plt.clabel()叠加等高线与密度图
- 频次直方分布图
- plt.hist()绘制一维频次直方分布图
- np.histogram()计数一维频次直方分布图
- plt.hist2d()绘制二维频次直方分布图
- np.histogram2d()计数二维频次直方分布图
- plt.hexbin()绘制正六边形分割
- KDE核密度估计
Matplotlib绘制简单图像
本章将讲解Matplotlib绘制简单图像:包括线图,散点图,基本误差线等一系列简单图像
线图
绘制线图其实用的就是plt.plot()函数,只需要传递给其每个数据点,并且指定数据点之间以线的方式连接,包括实线,虚线等等
x=np.arange(start=0,stop=10,step=0.5)
y=x**2+1
plt.plot(x,y)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Figure of y=x^2+1')
plt.show()
散点图
绘制散点图有两种方式,一种是使用plt.plot()函数,但是仅指定数据点显示格式但是不指定数据点间的连线方式,另外一种是使用plt.scatter()函数
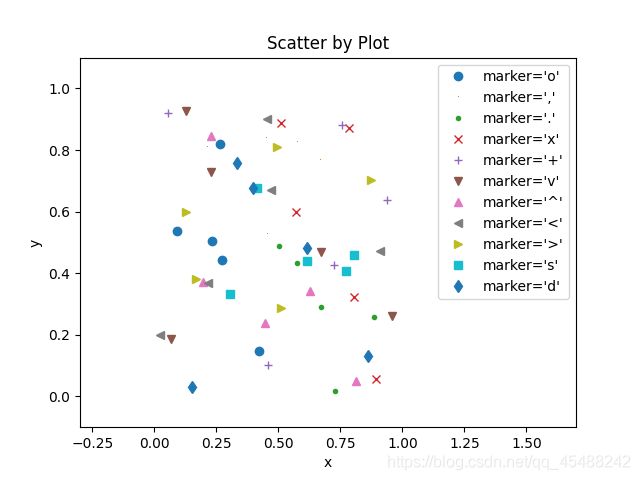
plt.plot绘制散点图
我们只要指定数据点的样式即可,具体的样式可以在官方文档中查到
for marker in ['o',',','.','x','+','v','^','<','>','s','d']:
plt.plot(np.random.random(5),np.random.random(5),marker,label="marker='{0}'".format(marker))
plt.legend(numpoints=1)
plt.xlim(-0.3,1.7)
plt.ylim(-0.1,1.1)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Scatter by Plot')
plt.show()
plt.scatter绘制散点图
plt.scatter专门用于绘制散点图的工具,他的功能相比于plot强大了不少
因为plt.scatter在创建散点图时具有更高的灵活性,能够单独控制每个点与数据匹配,还能够每个散点具有不同的属性(大小,表面颜色边框颜色等等)
下面我们使用plt.scatter来创建一个散点图,里面不同的数据点具有不同的颜色,为了能够,我们指定alpha参数来设置透明度,并且使用颜色条来表示数值与颜色之间的对应关系
rng=np.random.RandomState(0)
x=rng.randn(100)
y=rng.randn(100)
color=rng.randn(100)
sizes=1000*rng.rand(100)
plt.scatter(x,y,c=color,s=sizes,alpha=0.3,cmap='viridis')
plt.colorbar()
plt.show()
plt.sactter函数中数据点的给定和plt.plot一样,都是给所有数据点的x坐标值的列表和y坐标值的列表,plt.scatter函数将会自动匹配.
然后c参数是用于设置每个点的颜色的参数,所以大小必须和x或者y相等,s参数用于设置每个点的大小,因此大小也要匹配,最后我们指定cmap参数来设定散点见得颜色映射,用于区分不同的散点
除了上面的这几个参数外,我们还可以使用linewidth来指定边框宽度,edgecolor来指定边框颜色,使用marker参数来指定使用什么形状来表示数据点
最后在上面的程序中,我们还是用了plt.colorbar()来创建一个颜色条,表示颜色和数值之间的对应
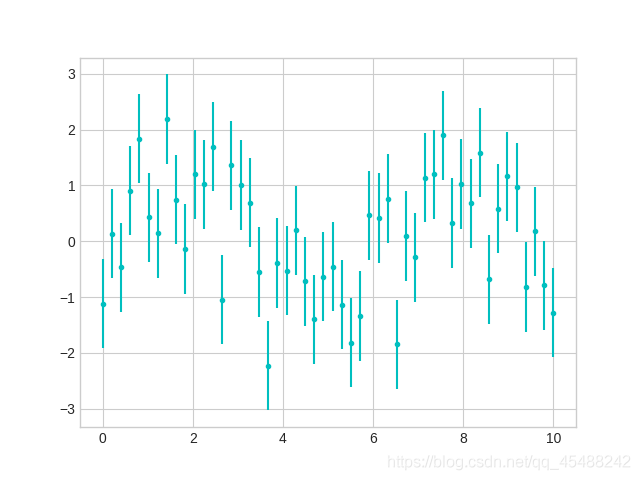
基本误差线
有的时候我们采集到的数据点并不是一个确定的值,而是具有一定精度的值,即具有误差范围,这个时候我们就可以通过基本误差线来表示该数据的范围
Matplotlib中基本误差线的创建可以使用plt.errorbar()函数创建,
plt.style.use('seaborn-whitegrid')
x=np.linspace(start=0,stop=10,num=50)
dy=0.8
y=np.sin(x)+dy*np.random.randn(50)
plt.errorbar(x,y,yerr=dy,fmt='.c')
plt.show()
上面y应该等于sin(x),但是我们为了体现基本误差线,我们人为的为y添加了由不确定性带来的误差dy*np.random.randn(50)
所以这里y就是一个具有误差的数据,因此我们需要用基本误差线来表示
基本误差线中给出数据点的方式和plot,scatter相同,yerr参数是指定误差的范围,fmt参数指定误差线和数据点的样式,指定格式和plot,scatter相同
此外plt.errorbar()函数还有许多可以用于改善图像外观的参数,例如:调整误差线颜色的ecolor,调整误差线宽度的elinewidth,用于设置边界横线大小的capsize参数
plt.style.use('seaborn-whitegrid')
x=np.linspace(start=0,stop=10,num=50)
dy=0.8
y=np.sin(x)+dy*np.random.randn(50)
# plt.plot(x,y,color='c')
plt.errorbar(x,y,yerr=dy,fmt='.c',ecolor='y',elinewidth=1,capsize=2)
plt.show()
密度图与等高线图
通常来说,如果我们需要绘制一张二维函数的图像,通常会选择在空间直角坐标系中来绘制.但是有的时候我们用颜色或者等高线来表示第三维的数据,将三维的图像简化为二维却会起到意想不到的效果.
所以本章将讲解如何实现上面的问题,即实现等高线图,在此基础上将进一步实现密度图.
Matplotlib中提供了三个函数完成等高线图,密度图的绘制:
- plt.contour()绘制等高线图
- plt.contourf()绘制带有填充色彩的等高线图
- plt.imshow()显示图形
首先需要说明的是,我们绘制三维图像(包括用二维表示的三维图像,如等高线图)时,每个输入的数据点都是(x,y)坐标对,因此我们此时不能像前面plt.plot()函数一样仅传入x和y数组,因为我们绘制三维图像时候输入的是网格点,因此需要用meshgrid()来配对x,y,生成一张网格
我们从数据结构的角度去理解,我们使用meshgrid()配对得到的
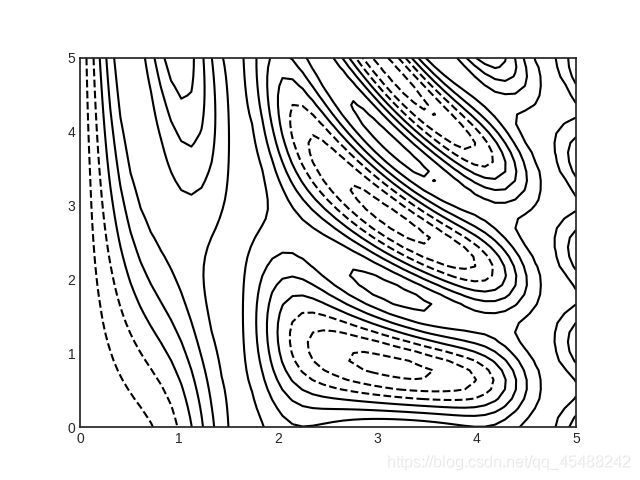
plt.contour()绘制等高线图
plt.contour()必须具备的三个值是x轴,y轴,z轴的网格数据,可以选择其他参数来调整结果
plt.style.use('seaborn-white')
x=np.linspace(0,5,50)
y=np.linspace(0,5,40)
X,Y=np.meshgrid(x,y)
Z=np.sin(X)**10+np.cos(10+X*Y)*np.cos(X)
'''
我们从数据结构的角度去理解,我们使用meshgrid()配对X,Y得到的Z,其实是一个字典型数据,网格点(X,Y)作为对应的Z的索引
'''
plt.contour(X,Y,Z,color='black')
plt.show()
注意:如果我们只给定一种颜色,那么默认会使用虚线表示负数
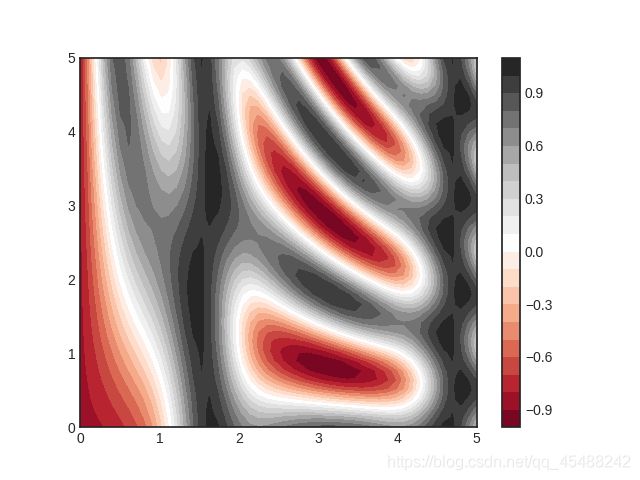
我们还可以指定plt.contour()函数的cmap参数来设置其他的线条颜色配置方案,并且可以传递一个参数来表示将所有Z值等分为20份,并根据数值大小自动分配颜色
plt.style.use('seaborn-white')
x=np.linspace(0,5,50)
y=np.linspace(0,5,40)
X,Y=np.meshgrid(x,y)
Z=np.sin(X)**10+np.cos(10+X*Y)*np.cos(X)
plt.contour(X,Y,Z,20,cmap='RdGy')
plt.show()
这里我们使用的是RdGy(红-灰配色)配色方案,这对于数据集中度的显示很好,如果依旧看不出来颜色和值的对应,我们使用plt.colorbar()调出色彩数值对应图即可
plt.style.use('seaborn-white')
x=np.linspace(0,5,50)
y=np.linspace(0,5,40)
X,Y=np.meshgrid(x,y)
Z=np.sin(X)**10+np.cos(10+X*Y)*np.cos(X)
plt.contour(X,Y,Z,20,cmap='RdGy')
plt.colorbar()
plt.show()
此外,所有支持的配色方案在颜色条的配置中将会在后面讲解
plt.contourf()绘制密度图
密度图和等高线图的区别就在于密度图以不同的色彩填充了等高线图,这样使得整个图过渡的好多了
plt.contourf()函数的用法和plt.contour()函数一模一样
plt.style.use('seaborn-white')
x=np.linspace(0,5,50)
y=np.linspace(0,5,40)
X,Y=np.meshgrid(x,y)
Z=np.sin(X)**10+np.cos(10+X*Y)*np.cos(X)
plt.contourf(X,Y,Z,20,cmap='RdGy')
plt.colorbar()
plt.show()
虽然plt.contourf()函数将等高线之间的空白用不同的色彩填充了起来,但是我们发现每两个颜色之间的过渡不是很好,这是因为图里的颜色的改变实际上是一个离散而非连续的过程
当然我们可以指定更多级的等高线,来实现平滑过渡,但是这样的效果并不好,因为matplotlib将会绘制出所有的等高线.为此,一个很好的解决方案就是plt.imshow()函数.他会将图片渲染成渐变图(虽然不是平滑的过渡)
plt.imshow()渲染渐变图像
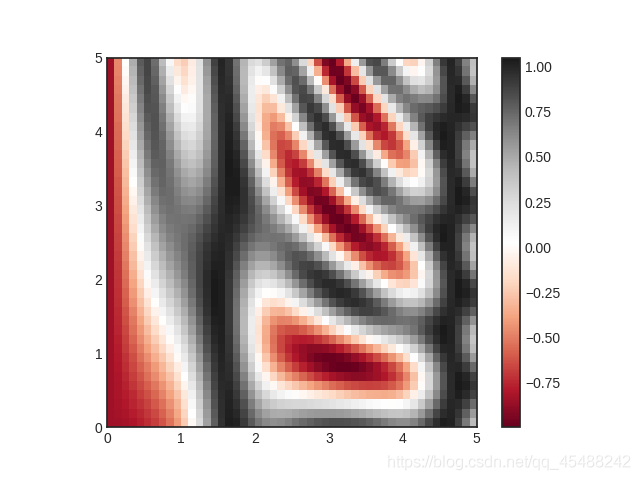
上面的问题在于我们得到的是颜色离散分布的图像,因此,我们可以使用plt.imshow()函数来渲染图像
我们需要为plt.imshow()传入计算得到的数组
plt.style.use('seaborn-white')
x=np.linspace(0,5,50)
y=np.linspace(0,5,40)
X,Y=np.meshgrid(x,y)
Z=np.sin(X)**10+np.cos(10+X*Y)*np.cos(X)
plt.imshow(Z,extent=[0,5,0,5],origin='lower',cmap='RdGy')
plt.colorbar()
plt.axis(aspect='image')
plt.show()
这里需要说明的是,plt.imshow()不能像plt.contour()和plt.contourf()函数一样,只需要给定x和y向量,就能够在内部实现plt.meshgrid()的自动配对
因此我们需要手动给extend参数以[xmin,xmax,ymin,ymax]的方式指定网格
我们指定网格后,还需要指定网格的哪个角作为作为坐标的原点.因为plt.imshow()默认是以左上角作为原点的,这样的话会导致坐标轴反向显示
所以指定origin参数为lower,设置左下角为原点
最后,我们指定了cmap参数来设置配色方案
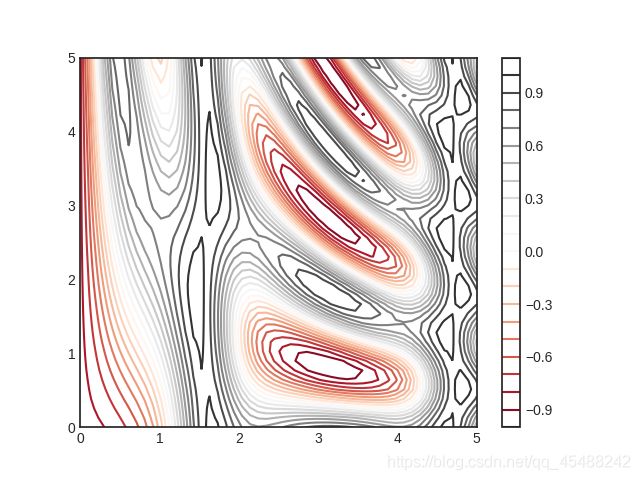
plt.clabel()叠加等高线与密度图
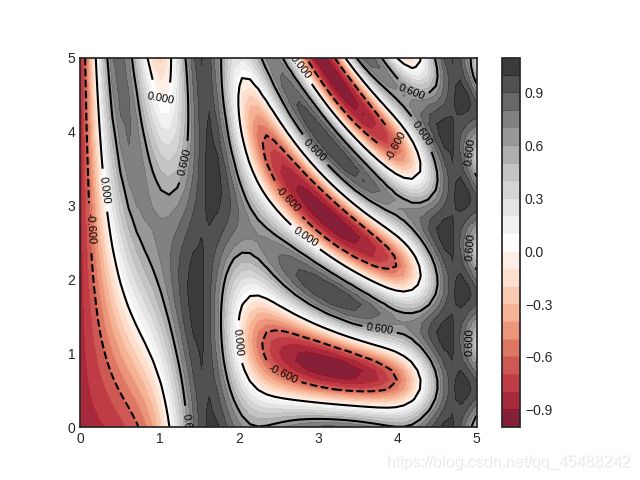
最后,我们可以使用plt.clabel()函数来实现等高线图和密度图的叠加
plt.style.use('seaborn-white')
x=np.linspace(0,5,50)
y=np.linspace(0,5,40)
X,Y=np.meshgrid(x,y)
Z=np.sin(X)**10+np.cos(10+X*Y)*np.cos(X)
contour=plt.contour(X,Y,Z,3,colors='black')
plt.clabel(contour,inline=True,fontsize=8)
plt.contourf(X,Y,Z,20,cmap='RdGy',alpha=0.9)
plt.colorbar()
plt.show()
当然我们也可以让等高线图和imshow()渲染之后的图像叠加,不过由于已经马赛克化了,效果还是密度图和等高线图叠加好
频次直方分布图
一个简单的频次直方分布图是了解数据的良好开端.对于仅含一个标签值的数据,我们可以绘制一个普通的频次直方分布图来直观的感受数据集中该标签值的分布程度.对于含有两个标签值的数据,我们实际上也可以绘制二维频次直方分布图来观察两个标签值的分布,.最后我们还将讲解另外一种用于估计数据出现次数的,从频次直方分布图衍生来的核密度估计方法
plt.hist()绘制一维频次直方分布图
我们只需要给plt.hist()传入标签数组,plt.hist()就会在后台帮我们统计传入数组中各个元素出现的频率,然后绘图
plt.style.use('seaborn')
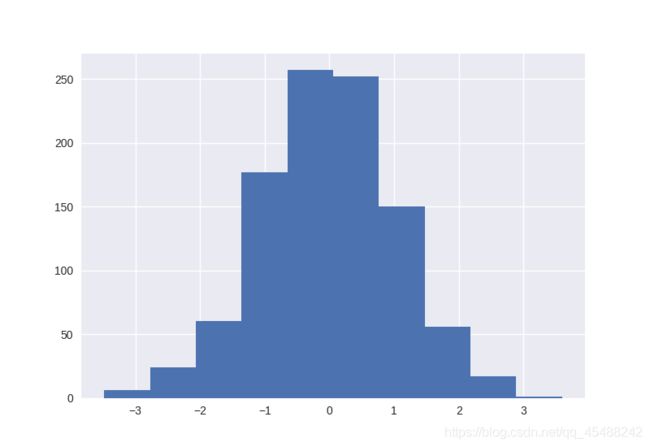
data=np.random.randn(1000)
plt.hist(data)
plt.show()
这里我们使用np.random.rand()函数来生成1000个正态分布的点
plt.hist()函数中还有许多用于调整计算过程和显示效果的选项,下面给出一个更加个性化的频次直方分布图
plt.style.use('seaborn')
data=np.random.randn(1000)
plt.hist(data,bins=30,alpha=0.5,histtype='stepfilled',color='steelblue',edgecolor='none')
plt.show()
这里我们指定使用30个分组,50%的透明度,每个柱子的样式为stepfilled,颜色为steelblue,边框颜色为无
得到效果如下
此外,如果我们需要将三个不同的标签值的频次直方分布图叠加在一起进行比较,我们将每个柱子的样式设置为stepfilled,同时将透明度alpha降低,这样的效果很不错
plt.style.use('seaborn')
data_1=np.random.normal(0,0.8,1000)
data_2=np.random.normal(-2,1,1000)
data_3=np.random.normal(3,2,1000)
kwargs=dict(histtype='stepfilled',alpha=0.3,bins=40,edgecolor='none')
plt.hist(data_1,**kwargs)
plt.hist(data_2,**kwargs)
plt.hist(data_3,**kwargs)
plt.show()
这里第七行是将各种参数转变为键值对的字典,因为在编写函数的时候,可能会收到不定长的指定参数值的形式
例如我们使用plt.hist()绘图的时候,以下两种形式都对:
- plt.hist(data),注意,data是一个不定长的数组
- plt.hist(data,alpha=0.3,bins=40),注意,除了data是不定长的数组外,指定的参数的数量也是不定的
总结下来,我们的函数可能会接受到: 1.不定长的数组 2.不定长的参数
不过我们使用alpha=0.3这类形式指定的参数都会被转化成键值对形式,即字典,所以实际上函数会接收到不定长的数组或者不定长的字典
所以为了解决由这两个输入带来的问题,Python使用了两种特定的参数*args和**kwargs
两者分别接受不定长的数组和不定长的字典而且名字是可以随便变的,只要*和**在就行
所以使用*a和**b是同一个效果,约定俗成不定长数组使用*args,不定长字典使用**kwargs
最后效果如下
np.histogram()计数一维频次直方分布图
plt.histogram()函数用于一维频次直方图的计数而不会绘制图像
Counts,Bins=np.histogram(np.random.normal(0,0.8,1000))
print(Counts)
print(Bins)
>>>
[ 1 11 55 146 250 282 170 72 11 2]
[-2.9878549 -2.4017661 -1.81567731 -1.22958851 -0.64349971 -0.05741091
0.52867788 1.11476668 1.70085548 2.28694428 2.87303308]
plt.hist2d()绘制二维频次直方分布图
和前面绘制等高线图一样,我们需要给plt.hist2d()函数传入两个已配对的网格点
这列我们使用多元高斯分布来生成网格点
plt.style.use('seaborn')
mean=[0,0]
cov=[[1,1],[1,2]]
x,y=np.random.multivariate_normal(mean,cov,10000).T
plt.hist2d(x,y,bins=30,cmap='Blues')
colorbar=plt.colorbar()
colorbar.set_label('Counts in bin')
plt.show()
np.histogram2d()计数二维频次直方分布图
和np.histogram()类似,np.histogram2d()用于计数二维频次直方分布图
mean=[0,0]
cov=[[1,1],[1,2]]
x,y=np.random.multivariate_normal(mean,cov,10000).T
Counts,Xedge,Yedge=np.histogram2d(x,y,bins=30)
print(Counts)
print(Xedge)
print(Yedge)
>>>
[[ 0. 0. 0. 1. 1. 0. 0. 1. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0.]
[ 0. 0. 0. 0. 0. 0. 1. 2. 0. 0. 0. 1. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0.]
[ 0. 0. 1. 1. 0. 0. 3. 0. 1. 0. 0. 0. 1. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0.]
[ 0. 0. 0. 0. 2. 2. 1. 3. 2. 3. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0.]
[ 1. 0. 2. 3. 2. 1. 4. 3. 4. 2. 3. 1. 1. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0.]
[ 0. 0. 1. 4. 5. 3. 8. 4. 8. 9. 2. 2. 2. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0.]
[ 0. 0. 0. 3. 4. 7. 11. 15. 17. 16. 11. 9. 7. 0.
1. 1. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0.]
[ 0. 0. 0. 0. 3. 8. 9. 17. 16. 22. 17. 12. 14. 6.
1. 2. 2. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0.]
[ 0. 1. 2. 3. 10. 9. 14. 16. 23. 35. 36. 31. 22. 17.
14. 4. 2. 1. 1. 2. 1. 0. 0. 0. 0. 0. 0. 0.
0. 0.]
[ 1. 1. 2. 0. 7. 7. 19. 21. 29. 34. 41. 43. 38. 34.
21. 11. 4. 4. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0.
0. 0.]
[ 0. 0. 0. 0. 1. 6. 13. 19. 31. 45. 72. 67. 51. 44.
28. 14. 7. 8. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0.
0. 0.]
[ 0. 0. 0. 0. 0. 5. 12. 18. 48. 59. 78. 86. 78. 73.
52. 31. 19. 17. 4. 2. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0.]
[ 0. 0. 0. 0. 1. 5. 11. 14. 30. 54. 61. 87. 119. 101.
78. 65. 36. 18. 6. 0. 3. 3. 0. 0. 0. 0. 0. 0.
0. 0.]
[ 0. 0. 0. 0. 1. 2. 7. 16. 29. 40. 73. 86. 97. 109.
97. 93. 59. 29. 24. 14. 3. 2. 1. 1. 0. 0. 0. 0.
0. 0.]
[ 0. 0. 0. 0. 0. 0. 3. 8. 17. 34. 51. 93. 101. 120.
112. 121. 79. 47. 33. 15. 7. 4. 1. 0. 1. 0. 0. 0.
0. 0.]
[ 0. 0. 0. 0. 1. 0. 0. 6. 13. 18. 45. 80. 102. 143.
138. 118. 96. 76. 53. 30. 12. 8. 3. 1. 0. 0. 0. 0.
0. 0.]
[ 0. 0. 0. 0. 0. 0. 3. 1. 4. 13. 39. 48. 84. 108.
120. 118. 140. 87. 70. 55. 28. 16. 6. 6. 0. 0. 0. 0.
0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 1. 6. 11. 22. 44. 42. 79.
114. 112. 120. 107. 74. 62. 43. 16. 7. 4. 2. 1. 0. 0.
0. 0.]
[ 0. 0. 0. 0. 0. 0. 1. 0. 2. 1. 10. 19. 30. 64.
90. 103. 117. 92. 86. 60. 33. 20. 6. 7. 3. 1. 1. 0.
0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 1. 5. 3. 16. 17. 24.
70. 77. 90. 73. 93. 69. 48. 23. 21. 1. 0. 2. 1. 0.
0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 1. 7. 11. 28.
40. 58. 69. 71. 67. 53. 58. 36. 18. 9. 4. 0. 0. 1.
0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 3. 6. 15.
19. 25. 38. 60. 52. 56. 40. 35. 17. 8. 3. 0. 0. 0.
1. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 1. 10.
8. 20. 23. 29. 48. 48. 42. 28. 19. 13. 6. 3. 0. 1.
1. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 2.
3. 12. 13. 15. 25. 23. 21. 24. 9. 8. 3. 3. 2. 0.
0. 1.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 1. 7. 15. 13. 16. 23. 11. 18. 8. 7. 3. 2. 1.
0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1.
1. 2. 3. 5. 11. 6. 9. 8. 6. 6. 5. 2. 1. 0.
0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
1. 1. 0. 3. 4. 2. 7. 13. 5. 3. 4. 2. 1. 2.
0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
1. 0. 0. 1. 2. 1. 2. 5. 5. 2. 4. 1. 2. 1.
0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 2. 0. 2. 2. 0. 1. 0. 0.
0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 2. 1. 2. 1. 0. 0.
0. 1.]]
[-3.72985369 -3.49534288 -3.26083208 -3.02632127 -2.79181047 -2.55729966
-2.32278886 -2.08827805 -1.85376725 -1.61925644 -1.38474564 -1.15023483
-0.91572403 -0.68121322 -0.44670242 -0.21219161 0.02231919 0.25683
0.4913408 0.72585161 0.96036241 1.19487322 1.42938402 1.66389483
1.89840563 2.13291644 2.36742724 2.60193805 2.83644885 3.07095966
3.30547046]
[-5.38714723 -5.02448129 -4.66181535 -4.29914941 -3.93648347 -3.57381754
-3.2111516 -2.84848566 -2.48581972 -2.12315379 -1.76048785 -1.39782191
-1.03515597 -0.67249003 -0.3098241 0.05284184 0.41550778 0.77817372
1.14083966 1.50350559 1.86617153 2.22883747 2.59150341 2.95416934
3.31683528 3.67950122 4.04216716 4.4048331 4.76749903 5.13016497
5.49283091]
plt.hexbin()绘制正六边形分割
我们使用plt.hist2d()来绘制二维频次直方图的话,每一个单元格都是正方形,我们可以使用plt.hexbin()来绘制每一个单元格都是六边形的二维频次直方分布图
mean=[0,0]
cov=[[1,1],[1,2]]
x,y=np.random.multivariate_normal(mean,cov,10000).T
plt.hexbin(x,y,bins=30,gridsize=30,cmap='Blues')
colorbar=plt.colorbar()
colorbar.set_label('Counts in bin')
plt.show()
KDE核密度估计
核密度估计实际上就是高斯分布来对频数直方分布图进行拟合,从而使频次直方分布图平滑
我们将使用scipy.stats中的guassian_kde方法来实现核密度估计
from scipy.stats import gaussian_kde
mean=[0,0]
cov=[[1,1],[1,2]]
x,y=np.random.multivariate_normal(mean,cov,10000).T
data=np.vstack([x,y])
kde=gaussian_kde(data)
xgrid=np.linspace(start=-3.5,stop=3.5,num=40)
ygrid=np.linspace(start=-6,stop=6,num=40)
Xgrid,Ygrid=np.meshgrid(xgrid,ygrid)
Z=kde.evaluate(np.vstack([Xgrid.ravel(),Ygrid.ravel()]))
plt .imshow(Z.reshape(Xgrid.shape),origin='lower',aspect='auto',extent=[-3.5,3.5,-6,6],cmap='Blues')
colorbar=plt.colorbar()
colorbar.set_label('Density')
plt.show()