ICLR 2019 Oral 论文 BigGAN 解读及源代码拆解

简称：BigGAN

全称：Large Scale GAN Training for High Fidelity Natural Image Synthesis

来源：ICLR 2019 Oral

一、概述

（一）概要说一下 BigGAN 的研究背景：
到 BigGAN 提出为止，虽然 GANs 在图像生成领域取得了很多显著的成果，但是在学习像 ImageNet 这类复杂的数据集的能力还不够，并且生成高分辨率、多样性的图像样本的效果也不太理想。

（二）概要说一下 BigGAN 的研究目的：
合成具有更高分辨率、更加多样性的图像样本

（三）概要说一下 BigGAN 做的事情：
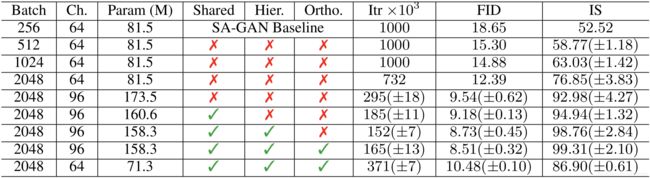
（1）首先，BigGAN 在基线模型 SA-GANs 的基础上增加每个批次的数据量为原来的2、4、8倍，发现增大每个批次训练数据的数量能够带来更好的效果；
（2）其次，增加每一层网络的通道数为先前工作的1.5倍，使网络参数的数量增加为原来的2~4倍，同样发现能够得到更好的效果；
（3）然后，为有效利用类别条件嵌入同时不增加参数数量，BigGANs 采用共享嵌入方法将类别条件线性投影到每个 BatchNorm 层的增益（gain）和偏置（bias），从而降低了计算和内存成本，提高了训练速度；
（4）紧接，为了从潜空间采用的随机噪声向量 z 能够直接影响不同分辨率及层次结构级别下的特征，BigGANs 通过层次化潜在空间将随机噪声向量 z 输入到生成器的每一层，从而降低了内存和计算成本，主要是降低了第一个线性层的参数数量；
（5）再次，BigGAN 研究工作探索了多种不同的随机噪声分布，并发现 {0,1} 伯努利分布和设限的正态分布(Censored Normal) 比从正态分布和均匀分布的效果更好，但由于截断技巧 比这两种分布的效果更好，而这两种分布并不适用截断技巧，因此 BigGAN 舍弃使用这两种分布而选择使用传统的正态分布，并通过截断技巧来权衡合成样本的保真度和多样性；
（6）其后，通过正交正则化来解决一些较大模型使用截断技巧造成的饱和伪影问题，将生成器调节平滑，强制使其适应截断技巧，从而更有效利用整个随机噪声向量空间合成更高质量的样本；
（7）最后，使用以上方法和技巧的虽然提高了模型的效果，但是模型在训练时也容易崩溃，所以在实际使用中需要采取提前停止训练的措施。针对这个问题，BigGANs 探索能够指示训练崩溃的度量指标，进一步分别研究和分析了生成器和判别器在大尺度下出现的不稳定性的原因，并提出了针对性的措施和解决方法。

（四）概览一下 BiGAN 的效果：
（1）512 x 512分辨率合成图像的效果

（2）初始分数（Inception Score）与弗雷歇初始距离（FID）的效果

	初始分数（IS）	弗雷歇初始距离（FID）	分辨率
真实图像	233		128*128
SAGAN	52.52	18.65	128*128
BigGAN	166.3	9.6	128*128
BigGAN	232.5	8.1	256*256
BigGAN	241.5	11.5	512*512

其中，初始分数（Inception Score，IS） 和弗雷歇初始距离（Fréchet Incepton Distance，FID）是目前评价 GANs 合成样本最常用的两个评价标准

• 初始分数（Inception Score，IS） 数值越大，GANs 合成的样本质量越高
• 弗雷歇初始距离（Fréchet Incepton Distance，FID）数值越小，GANs 合成的样本质量越高

二、核心方法

• 大批量
  每个批次训练数据的数量增加到 2048

• 大通道
  增加每一层网络的通道数为先前工作的1.5倍，使网络参数的数量增加为原来的2~4倍

• 共享嵌入
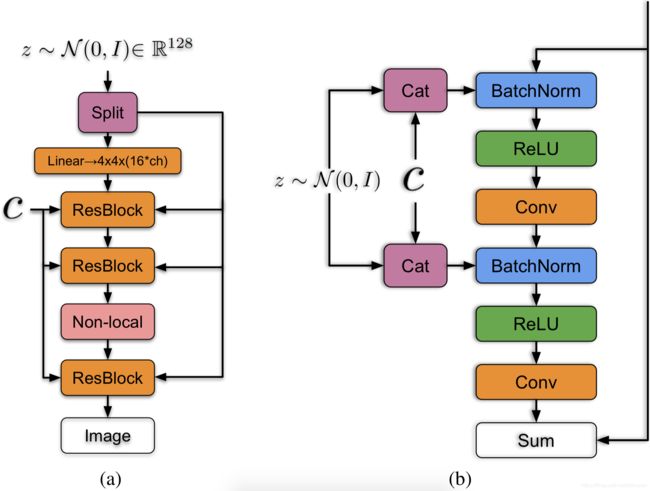
  类别条件线性投影到每个 BatchNorm 层的增益（gain）和偏置（bias），从而降低了计算和内存成本，提高了训练速度，而不是为每个嵌入分别设置单独一层，需要注意的是标签控制条件 c 并输入到第一层网络，如下图：
  

• 层次化潜在空间
  将随机噪声向量 z 对应不同的分辨率划分为多个块，然后将每一块随机噪声向量 z’ 与条件向量 c 连接在一起，再映射到 BatchNorm 层的增益（gain）和偏置（bias），如上图：

• 截断技巧
  通过重新采样数值高于选定阈值的值来截断 $z$ 矢量，减小 $z$ 的采样范围可以改善单个样品质量，但整体样品多样性，而增大 $z$ 的采样范围可以降低单个样品质量，而提高整体样品多样性。因此，可以通过阶段技巧来对样本的保真度和多样性进行细粒度地调节。

• 正交正则化
  一些较大的模型输入截断噪声向量 $z$ 是会产生饱和伪影，如下图所示：
  
  因此许多模型并不适合使用截断技巧。针对这种情况 BigGAN 通过正交正则化（Orthogonal Regularization）将 G 调节为平滑，强制使其适合使用截断技巧：
  $$R_{\beta }(W)=\beta {\Vert W^{T}W\odot (1-I)\Vert }_F^2$$
  其中，$W$ 为权重矩阵，$\beta$ 为超参数， $1$ 表示元素全为 1 的矩阵。
  BigGAN 这里所采用的正交正则化方法与传统的正交正则化是有区别的，从正则化中删除对角线项，从而最小化滤波器之间的成对余弦相似性，但并不限制它们的范数。

• 生成器的不稳定性及对策
  在 BigGAN 的大尺度批量和参数量的情况下，探索能够预示训练开始发生崩溃的标准，发现每一项权重的前三个最大的奇异值 ${\sigma }_0,{\sigma }_1,{\sigma }_2$ 最具信息量来做这件事情，并研究对生成器强加额外的条件防止谱的突爆问题。
  第一种方式，正则化每一项权重的最大奇异值 ${\sigma }_0$：接近一个固定值 ${\sigma }_{reg}$ 或第二大奇异值乘以某一比率 $r\cdot sg({\sigma }_1)$（其中，sg 表示停止梯度操作来防止正则化增加 ${\sigma }_1$ ）。
  第二种方式，或者采用偏奇异值分解（partial sigular value decomposition）来钳制 ${\sigma }_0$。
  给定权重 $W$，其第一个奇异向量为 ${\mu }_0$ 和 $v_0$，${\sigma }_{clamp}$ 表示钳制 ${\sigma }_0$ 的值，要么设置为 ${\sigma }_{reg}$，要么设置为$r\cdot sg({\sigma }_1)$，则权重被优化为：$$W=W-max(0,{\sigma }_0-{\sigma }_{clamp})v_0{u}_0^T$$
  这样处理权重后的效果就是：不管使用不用谱归一化（Spectral Normalization），上述技术都能够防止 ${\sigma }_0$ 或 $\frac{{\sigma }_0}{{\sigma }_1}$ 的逐渐增加至爆炸。
  但是文章也指出，在某情况下上述方法可以提高性能，但是并不能防止训练崩溃，这就表明调节生成器 G 可能改善稳定性，但并不足以保证稳定，因此将研究的关注点转到判别器上。

• 判别器的不稳定性及对策
  分析 D 的权重的谱曲线（论文中图 3b），与 G 不同，D 的谱是嘈杂的，$\frac{{\sigma }_0}{{\sigma }_1}$ 表现良好，并且奇异值在整个训练过程中一直增长，尽在崩溃时发生值跳跃而不是值爆炸。D 中谱出现的尖峰（spikes）噪声与训练不稳定有关，并探索 $R_1$ 领中心梯度惩罚来显式地正则化 D 的雅克比（Jacobian）的变化：
  $$R_1:=\frac{\gamma }{2}{\mathbb{E}}_{p_{\mathcal{D}}(x)}\left[\Vert \nabla D(x){\Vert }_F^2\right]$$
  通过降低惩罚强度 $\gamma$ 来提高训练稳定性，但同样会导致 IS 值下降。通过设置不同强度的正交正则化、DropOut、L2 等正则化策略的试验都证明：惩罚 D 的力度足够大时，训练就变得稳定，但是会严重牺牲性能。
  文章也通过在 ImageNet 上的训练与验证试验证明了 D 的损失在训练时趋于 0，但在崩溃时出现急剧增长的原因是 D 记忆了训练数据，但文章认为这符合 D 的角色，不显式地泛化，而是提炼训练数据并为生成器提供有用的训练信号。

三、实验

数据集
ImageNet ILSVRC 2012(128x128、256x256、512x512)、JFT-300M(更大、更复杂、更多样)、CIFAR-10(32323)图像超分辨率
结果

四、总结

1. BigGAN 最大的特色就是通过较大的批量数据以及较大的参数数量（增加通道数）来提高建模具有多种类别的复杂数据集（如 ImageNet），从而提高合成样本的质量（保真度和多样性）。
2. BigGAN 使用了很多技术和策略来提高合成样本的质量、平衡保真度与多样性、提高训练速度及稳定性等，整体来说是集现有 GANs 技术的一大作。
3. 分析了在大规模配置下， GANs 的不稳定性的来源，是 G 和 D 在对抗训练过程中的相互作用，而不是单独地来源于 G 或 D。并发现通过对 D 施加很强的约束可以稳定训练。通过现有的技术，通过放松约束调节并允许训练后期阶段发生崩溃，可以实现更好的效果。
4. 但 BigGANs 也存在一些不足：如：虽然大尺度提高合成样本的质量，但是也使模型容易不稳定，陷于完全崩溃的状态；虽然使用一些现有的策略和方法能够提高训练稳定，但不能彻底地避免崩溃；虽然对 D 施加较强的约束可以提高训练稳定性，但在性能上会造成很大的牺牲。
5. BigGAN 所采用的 batch_size = 2048 而取得的效果是是需要一定的硬件实力支撑的（BigGAN 的计算硬件：128 ~ 512 个核的 Google TPUv3 Pod）

五、源代码

作者正式非官方 PyTorch源码：https://github.com/ajbrock/BigGAN-PyTorch

层次化潜在空间（Hierarchical latent space) 和共享嵌入（Shared embedding）：

if self.hier:
      # 根据架构 arch 中 in_channels 的个数得到网络的层数，再加上最初始的 z 输入，从而确定将 z 划分的数量
      self.num_slots = len(self.arch['in_channels']) + 1
      # z 被划分后，每个小块的大小
      self.z_chunk_size = (self.dim_z // self.num_slots)
      # 根据 z 的每个小块的大小和数量确定最终的 z 的维度
      self.dim_z = self.z_chunk_size *  self.num_slots
      

# 在生成器中各层将噪声 z 与标签 y 连接
def forward(self, z, y):
	if self.hier:
		# 在指定的维度上对噪声 z 划分维 z_chunk_size 大小的多个块
		zs = torch.split(z, self.z_chunk_size, 1)
		# 网络第一层输入的随机噪声 z
    	z = zs[0]
    	# 将类别标签与各个噪声块相连
    	ys = [torch.cat([y, item], 1) for item in zs[1:]]


# 生成器网络中各个噪声块的具体使用 
# 将首个噪声切分块 z 作为网络的第一层输入（注意到：BigGAN 第一层仅输入了首个随机噪声切分块，而没有输入类别条件 c）
h = self.linear(z)
# 转换形状为 (batch_size, channel, width, width)
h = h.view(h.size(0), -1, self.bottom_width, self.bottom_width)
# 循环处理每一个 ResNet Block
for index, blocklist in enumerate(self.blocks):
	# 内层循环处理每一个 Block 的多层网络
	for block in blocklist:
		# 将上一层网络的输出、切分好的每一层网络对应的 z 与类别条件 y 的连接后的张量输入到 ResNet 的 Block 中
		h = block(h, ys[index])


# 查看 self.blocks
self.blocks = nn.ModuleList([nn.ModuleList(block) for block in self.blocks])

# 查看 self.blocks
# self.blocks 是模块的双层嵌套列表，外层列表是为了在指定分辨率上做不同 blocks 间的循环操作，内层类别是为了在某一 block 上做循环操作
self.blocks = []
for index in range(len(self.arch['out_channels'])):
	self.blocks += [[layers.GBlock(in_channels=self.arch['in_channels'][index], out_channels=self.arch['out_channels'][index], which_conv=self.which_conv, which_bn=self.which_bn, activation=self.activation, upsample=(functools.partial(F.interpolate, scale_factor=2) if self.arch['upsample'][index] else None))]]

# 再看一下 Generator 中的 ResNet block 内部如何处理上一层数据、与类别条件整合在一起的噪声块
# GBlock 类中定义，x 为上一层的输出（第一个 block 接收的是首个噪声块 z 经过全连接层后输出的张量）
def forward(self, x, y):
	# 上一层数据和带条件的噪声块输入到第一个 batch norm 层
	h = self.activation(self.bn1(x, y))
    if self.upsample:
	      h = self.upsample(h)
	      x = self.upsample(x)
    h = self.conv1(h)
    # 上一层数据和带条件的噪声块输入到第二个 batch norm 层
    h = self.activation(self.bn2(h, y))
    h = self.conv2(h)
    if self.learnable_sc:       
      x = self.conv_sc(x)
    return h + x

# 最后查看 batch norm 层到底如何处理上层数据及待条件控制的噪声块的，bn1 和 bn2 对应的 batch norm 层就是 layer.py 中 ccbn 类，表示 class conditional batch norm，也就是文章提到的共享嵌入（shared embedding）的方法，将
def forward(self, x, y):
    # Calculate class-conditional gains and biases
    gain = (1 + self.gain(y)).view(y.size(0), -1, 1, 1)
    bias = self.bias(y).view(y.size(0), -1, 1, 1)
    # If using my batchnorm
    if self.mybn or self.cross_replica:
      return self.bn(x, gain=gain, bias=bias)
    # else:
    else:
      if self.norm_style == 'bn':
        out = F.batch_norm(x, self.stored_mean, self.stored_var, None, None,
                          self.training, 0.1, self.eps)
      elif self.norm_style == 'in':
        out = F.instance_norm(x, self.stored_mean, self.stored_var, None, None,
                          self.training, 0.1, self.eps)
      elif self.norm_style == 'gn':
        out = groupnorm(x, self.normstyle)
      elif self.norm_style == 'nonorm':
        out = x
      return out * gain + bias


# 需要注意上面的 ccbn（class conditional batch norm）层中的 gain 和 bias 并不是某些博文中说的权重和偏置
# 查看 ccbn 类属性
self.gain = which_linear(input_size, output_size)
self.bias = which_linear(input_size, output_size)

# 查看这里的 which_linear，这里使用 python 的偏函数给 ccbn 类传入 bn_linear，
self.which_bn = functools.partial(layers.ccbn, which_linear=bn_linear, cross_replica=self.cross_replica, mybn=self.mybn, input_size=(self.shared_dim + self.z_chunk_size if self.G_shared else self.n_classes), norm_style=self.norm_style, eps=self.BN_eps)

# 查看 bn_linear
bn_linear = (functools.partial(self.which_linear, bias=False) if self.G_shared else self.which_embedding)

# 查看 which_linear，又是通过python 的偏函数使用 layers.py 中的 SNLinear
elf.which_linear = functools.partial(layers.SNLinear, num_svs=num_G_SVs, num_itrs=num_G_SV_itrs, eps=self.SN_eps)

# 查看 layers.py 中的 SNLinear
class SNLinear(nn.Linear, SN):
	def __init__(self, in_features, out_features, bias=True, num_svs=1, num_itrs=1, eps=1e-12):
    	nn.Linear.__init__(self, in_features, out_features, bias)
    	SN.__init__(self, num_svs, num_itrs, out_features, eps=eps)
    def forward(self, x):
    	return F.linear(x, self.W_(), self.bias)

# 查看用到谱归一化类 SN
# 最后查看 layers.py 中的谱归一化（Spectral normalization）基类
class SN(object):
  def __init__(self, num_svs, num_itrs, num_outputs, transpose=False, eps=1e-12):
    # Number of power iterations per step
    self.num_itrs = num_itrs
    # Number of singular values
    self.num_svs = num_svs
    # Transposed?
    self.transpose = transpose
    # Epsilon value for avoiding divide-by-0
    self.eps = eps
    # Register a singular vector for each sv
    for i in range(self.num_svs):
      self.register_buffer('u%d' % i, torch.randn(1, num_outputs))
      self.register_buffer('sv%d' % i, torch.ones(1))
  
  # Singular vectors (u side)
  @property
  def u(self):
    return [getattr(self, 'u%d' % i) for i in range(self.num_svs)]

  # Singular values; 
  # note that these buffers are just for logging and are not used in training. 
  @property
  def sv(self):
   return [getattr(self, 'sv%d' % i) for i in range(self.num_svs)]
   
  # Compute the spectrally-normalized weight
  def W_(self):
    W_mat = self.weight.view(self.weight.size(0), -1)
    if self.transpose:
      W_mat = W_mat.t()
    # Apply num_itrs power iterations
    for _ in range(self.num_itrs):
      svs, us, vs = power_iteration(W_mat, self.u, update=self.training, eps=self.eps) 
    # Update the svs
    if self.training:
      with torch.no_grad(): # Make sure to do this in a no_grad() context or you'll get memory leaks!
        for i, sv in enumerate(svs):
          self.sv[i][:] = sv     
    return self.weight / svs[0]

六、附录

BigGAN 探索可用的潜空间：
gongchang

• 正太分布：$\mathcal{N}(0,I)$
• 均与分布：$\mathcal{U}[-1,1]$
• 伯努利分布：Bernoulli{0,1}
• 截取正太分布：$max(\mathcal{N}(0,I))$
• $-1,0,1$独立类别，以相同概率采样
• $\mathcal{N}(0,I)$ 乘以 Bernoulli{0,1}
• $\mathcal{N}(0,I)$ 连接 Bernoulli{0,1}
• 方差退火$\mathcal{N}(0,\sigma I)$
• 各样本可变方差：$\mathcal{N}(0,{\sigma }_{i}I)$，其中${\sigma }_i\sim \mathcal{U}[{\sigma }_l,{\sigma }_h]$

（未截止。。。待续。。。）