算法中的排序问题总结，时间复杂度为O(n)的排序，计数排序，桶排序，基数排序

线性时间的排序算法

大学时学过的一些排序算法，像插入排序（直接插入排序，折半插入排序，希尔排序）、交换排序（冒泡排序，快速排序）、选择排序（简单选择排序，堆排序）、2-路归并排序（见我的另一篇文章：各种内部排序算法的实现）等，这些排序算法都有一个共同的特点，就是基于两两比较交换位置。本文将介绍三种非比较的排序算法：计数排序，基数排序，桶排序。它们将突破比较排序的Ω(nlgn)下界，以线性时间运行。

可以点击查看比较排序算法动图，快速预习复习一下各种比较排序算法

有博主总结的非常好，推荐这个
https://blog.csdn.net/yushiyi6453/article/details/76407640

一、比较排序算法的时间下界

• 所谓的比较排序是指通过比较来决定元素间的相对次序。
• “定理：对于含n个元素的一个输入序列，任何比较排序算法在最坏情况下，都需要做Ω(nlgn)次比较。”
  也就是说，比较排序算法的运行速度不会快于nlgn，这就是基于比较的排序算法的时间下界。
  
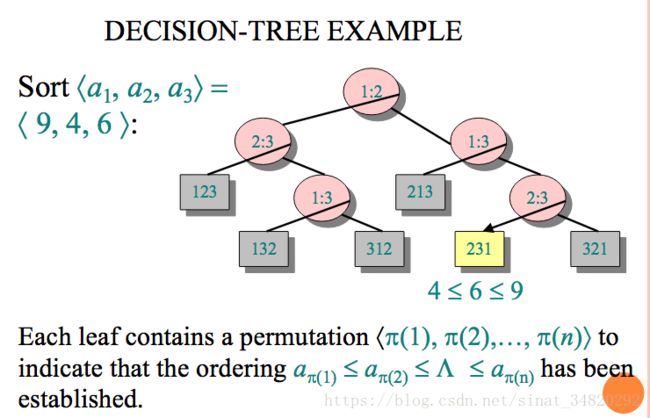
• 通过决策树（Decision-Tree）可以证明这个定理，决策树的叶子代表可能的排序结果，则树的高度就是比较排序的最多比较次数，n个元素的二叉决策树有n!个不重复叶子节点（每个叶子结点代表一个排序结果，可能的排序结果时n的排列组合，故有n!个），n!个叶子节点的二叉树的高度h=Ω(nlgn)，推导如下图。关于决策树的定义以及证明过程，推荐观看《MIT公开课：线性时间排序》。
  
• 根据上面的证明，我们知道任何比较排序算法的运行时间不会快于nlgn。那么我们是否可以突破这个限制呢？当然可以，接下来我们将介绍三种线性时间的排序算法，它们都不是通过比较来排序的，因此，下界Ω(nlgn)对它们不适用。

二、计数排序（Counting Sort）

计数排序的基本思想就是对每一个输入元素x，确定小于x的元素的个数，这样就可以把x直接放在它在最终输出数组的位置上，例如要对下面的数组A排序：

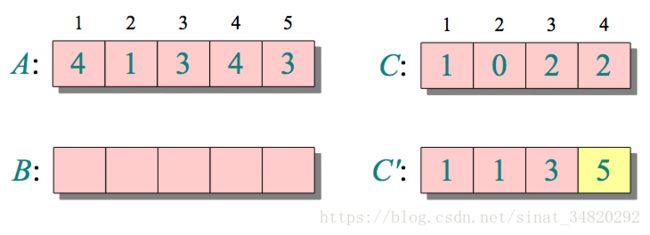
算法的步骤大致如下：

1. 找出待排序的数组中最大和最小的元素，得到值域表C

2. 统计数组中每个值为i的元素出现的次数，存入数组C的第i项

3. 对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加，加完后如C’所示）

4. 反向填充目标数组B：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1(插一句嘴，反向填充的妙处在于排列出来的是稳定的Stable)
   C++代码：

/************************************************************************* 
    > File Name: CountingSort.cpp 
    > Author: SongLee 
    > E-mail: [email protected] 
    > Created Time: 2014年06月11日 星期三 00时08分55秒 
    > Personal Blog: http://songlee24.github.io 
 ************************************************************************/  
#include  
using namespace std;  
  
/* 
 *计数排序：A和B为待排和目标数组，k为数组中最大值,len为数组长度 
 */  
void CountingSort(int A[], int B[], int k, int len)  
{  
    int C[k+1];  
    for(int i=0; i<k+1; ++i)  
        C[i] = 0;  
    for(int i=0; i<len; ++i)  
        C[A[i]] += 1;  
    for(int i=1; i<k+1; ++i)  
        C[i] = C[i] + C[i-1];  
    for(int i=len-1; i>=0; --i)  
    {  
        B[C[A[i]]-1] = A[i];  
        C[A[i]] -= 1;  
    }  
}  
  
/* 输出数组 */  
void print(int arr[], int len)  
{  
    for(int i=0; i<len; ++i)  
        cout << arr[i] << " ";  
    cout << endl;  
}  
  
/* 测试 */  
int main()  
{  
    int origin[8] = {4,5,3,0,2,1,15,6};  
    int result[8];  
    print(origin, 8);  
    CountingSort(origin, result, 15, 8);  
    print(result, 8);  
    return 0;  
}  

当输入的元素是0到k之间的整数时，时间复杂度是O(n+k)，空间复杂度也是O(n+k)。当k不是很大并且序列比较集中时，计数排序是一个很有效的排序算法。计数排序是一个稳定的排序算法。
可能你会发现，计数排序似乎饶了点弯子，比如当我们刚刚统计出C，C[i]可以表示A中值为i的元素的个数，此时我们直接顺序地扫描C，就可以求出排序后的结果。的确是这样，不过这种方法不再是计数排序，而是桶排序，确切地说，是桶排序的一种特殊情况。

三、桶排序（Bucket Sort）

桶排序（Bucket Sort）的思想是将数组分到有限数量的桶子里。每个桶子再个别排序（有可能再使用别的排序算法，一般使用简易并且稳定的插入排序）。当要被排序的数组内的数值是均匀分配的时候，桶排序可以以线性时间运行。桶排序过程动画演示：Bucket
Sort，桶排序原理图如下：

C++代码：

/************************************************************************* 
    > File Name: BucketSort.cpp 
    > Author: SongLee 
    > E-mail: [email protected] 
    > Created Time: 2014年06月11日 星期三 09时17分32秒 
    > Personal Blog: http://songlee24.github.io 
 ************************************************************************/  
#include  
using namespace std;  
  
/* 节点 */  
struct node  
{  
    int value;  
    node* next;  
};  
  
/* 桶排序 */  
void BucketSort(int A[], int max, int len)  
{  
    node bucket[len];  
    int count=0;  
    for(int i=0; i<len; ++i)  
    {  
        bucket[i].value = 0;  
        bucket[i].next = NULL;  
    }  
      
    for(int i=0; i<len; ++i)  
    {  
        node *ist = new node();  
        ist->value = A[i];  
        ist->next = NULL;  
        int idx = A[i]*len/(max+1); // 计算索引  
        if(bucket[idx].next == NULL)  
        {  
            bucket[idx].next = ist;  
        }  
        else /* 按大小顺序插入链表相应位置 */  
        {  
            node *p = &bucket[idx];  
            node *q = p->next;  
            while(q!=NULL && q->value <= A[i])  
            {  
                p = q;  
                q = p->next;  
            }  
            ist->next = q;  
            p->next = ist;  
        }  
    }  
  
    for(int i=0; i<len; ++i)  
    {  
        node *p = bucket[i].next;  
        if(p == NULL)  
            continue;  
        while(p!= NULL)  
        {  
            A[count++] = p->value;  
            p = p->next;  
        }  
    }  
}  
  
/* 输出数组 */  
void print(int A[], int len)  
{  
    for(int i=0; i<len; ++i)  
        cout << A[i] << " ";  
    cout << endl;  
}  
  
/* 测试 */  
int main()  
{  
    int row[11] = {24,37,44,12,89,93,77,61,58,3,100};  
    print(row, 11);  
    BucketSort(row, 235, 11);  
    print(row, 11);  
    return 0;  
}  

四、基数排序（Radix Sort）

基数排序（Radix Sort）是一种非比较型排序算法，它将整数按位数切割成不同的数字，然后按每个位分别进行排序。基数排序的方式可以采用MSD（Most significant digital）或LSD（Least significant digital），MSD是从最高有效位开始排序，而LSD是从最低有效位开始排序。
当然我们可以采用MSD方式排序，按最高有效位进行排序，将最高有效位相同的放到一堆，然后再按下一个有效位对每个堆中的数递归地排序，最后再将结果合并起来。但是，这样会产生很多中间堆。所以，通常基数排序采用的是LSD方式。
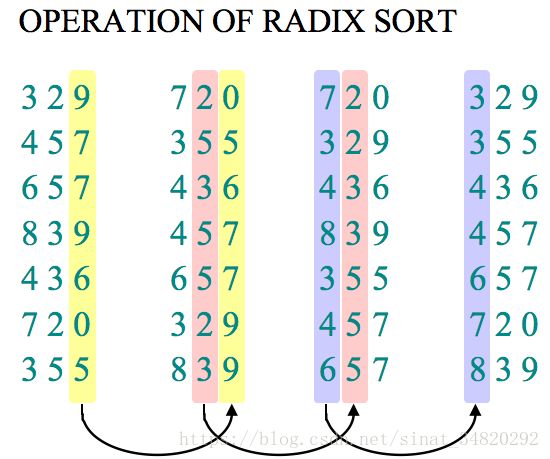
LSD基数排序实现的基本思路是将所有待比较数值（正整数）统一为同样的数位长度，数位较短的数前面补零。然后，从最低位开始，依次进行一次排序。这样从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列。需要注意的是，对每一个数位进行排序的算法必须是稳定的，否则就会取消前一次排序的结果。通常我们使用计数排序或者桶排序作为基数排序的辅助算法。可以查看基数排序的动画来帮助理解,动画中的每一轮排序实际上是二中的计数排序，计数排序没理解也可以参考这个动画理解。

如下图的基数排序的例子，采用LSD策略，把三位数字的三个数位作为三个排序的参数，实际问题中可能是三个不相关的具有不同排序地位的属性，如sql中：ORDER BY age DESC , weight DESC , score ASC （当然，SQL中的排序是LSD还是MSD的不得而知）

C++实现（使用计数排序）：

/************************************************************************* 
    > File Name: RadixSort.cpp 
    > Author: SongLee 
    > E-mail: [email protected] 
    > Created Time: 2014年06月22日 星期日 12时04分37秒 
    > Personal Blog: http://songlee24.github.io 
 ************************************************************************/  
#include  
using namespace std;  
  
// 找出整数num第n位的数字  
int findIt(int num, int n)  
{  
    int power = 1;  
    for (int i = 0; i < n; i++)  
    {  
        power *= 10;  
    }  
    return (num % power) * 10 / power;  
}  
  
// 基数排序（使用计数排序作为辅助）  
void RadixSort(int A[], int len, int k)  
{  
    for(int i=1; i<=k; ++i)  
    {  
        int C[10] = {0};   // 计数数组  
        int B[len];        // 结果数组  
  
        for(int j=0; j<len; ++j)  
        {  
            int d = findIt(A[j], i);  
            C[d] += 1;  
        }  
  
        for(int j=1; j<10; ++j)  
            C[j] = C[j] + C[j-1];  
  
        for(int j=len-1; j>=0; --j)  
        {  
            int d = findIt(A[j], i);  
            C[d] -= 1;  
            B[C[d]] = A[j];  
        }  
          
        // 将B中排好序的拷贝到A中  
        for(int j=0; j<len; ++j)  
            A[j] = B[j];  
    }  
}  
  
// 输出数组  
void print(int A[], int len)  
{  
    for(int i=0; i<len; ++i)  
        cout << A[i] << " ";  
    cout << endl;  
}  
  
// 测试  
int main()  
{  
    int A[8] = {332, 653, 632, 5, 755, 433, 722, 48};  
    print(A, 8);  
    RadixSort(A, 8, 3);  
    print(A, 8);  
    return 0;  
}  

基数排序的时间复杂度是 O(k·n)，其中n是排序元素个数，k是数字位数。注意这不是说这个时间复杂度一定优于O(nlgn)，因为n可能具有比较大的系数k。
另外，基数排序不仅可以对整数排序，也可以对有多个关键字域的记录进行排序。例如，根据三个关键字年、月、日来对日期进行排序。

---

本文修改自 TaoTaoFu 的CSDN 博客 ，原地址请点击：
https://blog.csdn.net/taotaofu/article/details/69062323?utm_source=copy