最短路径详解

最短路径：一个图里有很多边，每条边有权值，两点之间的权值最小的路径。
负权回路：一个环（某点出发走了一圈还回到原点）里的权值和为负数（环里的每个权值可正可负，但和为负）。
首先，存在负权回路的图里没有最短路，因为只要一直走这个回路就可以达到无限短。所以以下算法都是基于无负权回路的前提下。
算法验证：用HDU 2544 最短路提交能对就认为代码正确。

---

Floyd-Warshall

• 适用范围：无负权回路即可，边权可正可负，运行一次算法即可求得任意两点间最短路
• 时间复杂度：O(n^3)

定义dp[i][j]：i到j的最短路径，则在初始化dp的原图数据后，核心代码就这么短

void floyd() {
    for (int k = 1; k <= n; ++k) {
        for (int i = 1; i <= n; ++i) {
            for (int j = 1; j <= n; ++j) {
                dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j]);
            }
        }
    }
}

千万别以为k代表的是除i,j外的第三个点，要这么以为的话代码中的k循环应该在最里面， 即对每对(i,j)选择一个第三点k中转，但这样结果是错的。那k代表什么？往下看。

原理

打开算法导论（英文版）第693页看看，我知道你不想看英文，所以看下面的个人理解和翻译。

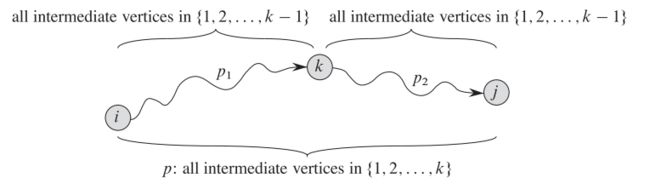
假定结点集V为{1,2..n}，对于 (i, j) 这条路，我们考虑它中途经过一些结点的所有情况（这些结点都取自集合{1,2,..k}），然后定义路径p为所有情况里的最短路径（即我们要找的答案路径）。那么关于k的p的关系有两种：

1. k不在 最短路径p 里，即p里的点都是{1,2,..k-1}的点，则显然(i, j)经过{1,2,..k}的最短路 和 经过{1,2,..k-1}的最短路是一样的。
2. k在 最短路径p 里，则p里的点都是{1,2,..k}的点，那我们可以把p分为(i,k)和(k,j)，这两条分出来路径的只含{1,2,..k-1}，因为p是最短路径，而k又在p里，所以(i,k)和(k,j)都是相对于(i,j)的最短路径 【此处算导没给证明，我们先假定自己认可这个结论】

根据上面的两种情况我们就可以得出递推式子

d(k)ij={wijifk=0min(d(k−1)ij,d(k−1)ik+d(k−1)kj)ifk≥1 d i j ( k ) = { w i j i f k = 0 m i n ( d i j ( k − 1 ) , d i k ( k − 1 ) + d k j ( k − 1 ) ) i f k ≥ 1

注意k是集合大小，不是经过的点个数，k=0的时候是不经过任何中间点的情况，k>=1表示经过{1,2..k}这个集合里的点集。没看懂式子的话再看下那两种情况，看懂的话我们发现需要三维数组才能表示这种 d(k)ij d i j ( k ) ，但在式子中我们的(k)其实只用在递推上，所以在上面代码中我们把k循环放在最外面就可以确保在计算 d(k)ij d i j ( k ) 前 dp[i][j]存的是 d(k−1)ij d i j ( k − 1 ) ，同理 d(k−1)ik d i k ( k − 1 ) 和 d(k−1)ik d i k ( k − 1 ) 也是一样。这点也就类似背包的二维压成一维。

实现

1. dp数组对于不存在的边初始化为无穷大，但直接用INT_MAX的话在dp[i][k] + dp[k][j]的时候溢出，所以精确来说设置 为比全部路径的最大值大一点就行，如10条最大1000的边则设置为10*1000+1，但为写代码方便就用0x3f3f3f3f (大概10亿）比较适合。
2. dp[i][i]初始化为0，即使就做题而言可能不会WA。

#include 
#include 
using namespace std;
const int maxn = 105;
const int inf = 0x3f3f3f3f;
int n,m;
int dp[maxn][maxn];

void floyd() {
    for (int k = 1; k <= n; ++k) {
        for (int i = 1; i <= n; ++i) {
            for (int j = 1; j <= n; ++j) {
                dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j]);
            }
        }
    }
}

int main(){
    int a,b,c;
    while(cin>>n>>m,n||m){
        memset(dp,inf,sizeof(dp));
        for (int i = 1; i <= n; ++i){  
            dp[i][i] = 0;       //不是必要
        }
        for (int i = 1; i <= m; ++i){
            cin>>a>>b>>c;
            dp[a][b] = dp[b][a] = c;
        }
        floyd();
        cout<1][n]<return 0;
}

---

Dijkstra

通俗翻译为迪杰斯特拉算法
- 适用范围：无负权回路，边权必须非负，单源最短路
- 时间复杂度：优化前O( n2 n 2 )

简单粗暴的原理

更新：2018-02-21
求t 点到s点的距离，假设距离s点最近的点p1距离为L，那么这个点一定是最短的，因为不可能有比直达最近的点还近的路，那么选它没错。

然后把s和点p1看成一个点S’，再同理选距离S’最近的点（其实这里实际求的是距离最开始的源点s），就这样一直重复操作贪心下去即可。

其中在选了p1之后我们要更新所有p1点相邻点到s点的最短距离，因为选p1点那么可能经过p1点到s点比原本的点直接到s点更近。

注意求点距离的时候求的是距离源点s最近，不是距离集合S’最近，距离集合S’最近就是最小生成树Prim算法了。

过程

数组dis[u]表示u到s点的最短距离。
我们一直找点u = min{ dis[k] , k点未访问 }，这个点就是最短路上的点，然后根据其他点v跟u点的关系去更新下dis[v]，不断重复找和更新即可。
dis[s]=0将源点加入最短路，然后循环n-1次每次找出一个最短路上的点，找的方法是直接找出剩下的点中dis[ ]最小的那个点u，u点就是最短路上的点，然后看看其他点v到s点的距离会不会因为这个u点的加入而改变，即若dis[v] > dis[u] + distance[u][v] 则更新dis[v]为 dis[u] + distance[u][v]。

实现

最基础的实现是邻接矩阵（二维数组），然后在找最小的dis[]部分可以用优先队列/最小堆优化查找速度。

#include 
#include 
using namespace std;

const int maxn = 105;
const int inf = 0x3f3f3f3f;
int dis[maxn];
bool vis[maxn];
int map_dis[maxn][maxn];
int n,m;
int dijkstra(int s, int t) {
    memset(vis, false, sizeof(vis));
    for (int i = 1; i <= n; ++i) {      //初始化各点到s点的距离
        dis[i] = map_dis[s][i];
    }
    dis[s] = 0, vis[s] = true;

    for (int i = 0; i < n - 1; ++i) {   //除s点外找n-1个点
        int u, tmin = inf;
        for (int j = 1; j <= n; ++j){   //找min{dis[]}
            if(!vis[j] && dis[j] < tmin){
                tmin = dis[j];
                u = j;
            }
        }
        // if(tmin == inf) return -1;   //无最短路
        vis[u] = true;                  //进入T集合
        for (int v = 1; v <= n; ++v){   //更新相邻点
            if(!vis[v] && dis[u] + map_dis[u][v] < dis[v]){
                dis[v] = dis[u] + map_dis[u][v];
            }
        }
    }
    return dis[t];
}

int main() {
    int a, b, c;
    while (cin >> n >> m, n || m) {
        memset(map_dis,inf,sizeof(map_dis));
        for (int i = 1; i <= m; ++i) {
            cin >> a >> b >> c;
            map_dis[a][b] = map_dis[b][a] = c;
        }
        cout << dijkstra(1,n) << endl;
    }
    return 0;
}

---

Spfa

Shortest Path Faster Algorithm，是国内原创算法，作者：西南交通大学段凡丁。
- 适用范围：边权可正可负，单源最短路，还可以判断图中有无负权回路
- 时间复杂度：O(kE)，k非常数，一般认为是所有点的平均入列次数且k一般小于等于2

原理

算法思路很简单，将源点加入队列，然后不断从队列中弹出顶点u，遍历u的邻接点v进行松弛更新（若dis[v] < dis[u] + distance[u][v] 则更新dis[v]为dis[u] + distance[u]），更新后如果v点不在队列里则进入队列。

证明

每次将点放入队尾，都是经过松弛操作达到的。换言之，每次的优化将会有某个点v的最短路径估计值dis[v]变小。所以算法的执行会使dis越来越小。由于我们假定图中不存在负权回路，所以每个结点都有最短路径值。因此，算法不会无限执行下去，随着d值的逐渐变小，直到到达最短路径值时，算法结束，这时的最短路径估计值就是对应结点的最短路径值。（证毕）

实现

算法思路本身是队列，不过也可以用栈。
队列方案判断负权环：如果某点进入队列的次数 > n次。
栈方案判断负权环：如果某点进入栈的次数 >= 2，栈方法判负环比较高效。

#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;

const int maxn = 105;
const int maxm = 10000;
const int inf = 0x3f3f3f3f;
int inq[maxn], head[maxn], dis[maxn];   //inq[u]==1:u在队列里
struct Edge{
    int v, w, next;
} edge[maxm * 2];
int cnt;
void add_edge(int u, int v, int w){ //邻接表前插法
    edge[cnt].v = v; edge[cnt].w = w; edge[cnt].next = head[u]; head[u] = cnt++;
}
void init(int n){
    cnt = 0;
    memset(head, -1, sizeof(head));
    memset(inq, 0, sizeof(inq));
    memset(dis, inf, sizeof(dis));
}
int spfa(int s, int t){
    queue<int>q;
    q.push(s);
    dis[s] = 0;
    inq[s] = 1;
    while (!q.empty()){
        int u = q.front(); q.pop();
        inq[u] = 0;
        for (int i = head[u]; i != -1; i = edge[i].next) {
            int v = edge[i].v;
            int w = edge[i].w;
            if (dis[v] > dis[u] + w){
                dis[v] = dis[u] + w;
                if (!inq[v]){
                    inq[v] = 1;
                    q.push(v);
                }
            }
        }
    }
    return dis[t];
}

int main() {
    int n, m, a, b, c;
    while (cin >> n >> m, n || m) {
        init(n);
        for (int i = 0; i < m; ++i) {
            cin >> a >> b >> c;
            add_edge(a, b, c);
            add_edge(b, a, c);
        }
        cout << spfa(1, n) << endl;
    }
    return 0;
}

队列式判断负权环

bool spfa(int s, int t){
    queue<int>q;
    q.push(s);
    dis[s] = 0;
    inq[s] = 1;
    times[s]++;
    while (!q.empty()){
        int u = q.front(); q.pop();
        inq[u] = 0;
        for (int i = head[u]; i != -1; i = edge[i].next) {
            int v = edge[i].v;
            int w = edge[i].w;
            if (dis[v] > dis[u] + w){
                dis[v] = dis[u] + w;
                if (!inq[v]){
                    inq[v] = 1;
                    q.push(v);
                    times[v]++;
                    if(times[v] > n){
                        return false;
                    }
                }
            }
        }
    }
    return true;
}

---

Bellman-Ford

• 适用范围：边权可正可负，单源最短路，还可以判断图中有无负权回路
• 时间复杂度：O(VE)，巨慢

Dijkstra算法以贪心法选取未被处理的具有最小权值的节点，然后对其的出边进行松弛操作；而Bellman-Ford简单地对所有边进行松弛操作

BELLMAN-FORD(G, w, s)
1   INITIALIZE-SINGLE-SOURCE(G, s)
2   for i ← 1 to |V[G]| - 1
3       do for each edge (u, v) ∈ E[G]
4              do RELAX(u, v, w)
5   for each edge (u, v) ∈ E[G]
6       do if d[v] d[u] + w(u, v)
7             then return FALSE
8  return TRUE

因为效率实在是很低，就不多介绍了