0.目录
1.递归的思想
2.递归的应用
- 2.1 单向链表的转置
- 2.2 单向排序链表的合并
- 2.3 汉诺塔问题
- 2.4 全排列问题
- 2.5 逆序打印单链表中的偶数结点
- 2.6 八皇后问题
3.小结
1.递归的思想
递归是一种数学上分而自治的思想：
- 将原问题分解为规模较小的问题进行处理
- 分解后的问题与原问题的类型完全相同，但规模较小
- 通过小规模问题的解，能够轻易求得原问题的解
- 问题的分解是有限的 ( 递归不能无限进行 )
- 当边界条件不满足时，分解问题 ( 递归继续进行 )
- 当边界条件满足时，直接求解 ( 递归结束 )
递归模型的一般表示法：
递归在程序设计中的应用：
- 递归函数
- 函数体中存在自我调用的函数
- 递归函数必须有递归出口 ( 边界条件 )
- 函数的无限递归将导致程序崩溃
递归思想的应用：
- 求解：Sum( n ) = 1 + 2 + 3 + ... + n
递归求和：
unsigned int sum(unsigned int n)
{
if( n > 1 )
{
return n + sum(n-1);
}
else
{
return 1;
}
}斐波拉契数列：
数列自身递归定义：1, 1, 2, 3, 5, 8, 13, 21, ...
斐波拉契数列：
unsigned int fac(unsigned int n)
{
if( n > 2 )
{
return fac(n-1) + fac(n-2);
}
if( (n == 2) || (n == 1) )
{
return 1;
}
return 0;
}用递归的方法编写函数求字符串长度：
用递归的方法编写函数求字符串长度：
unsigned int _strlen_(const char* s)
{
if( *s != '\0' )
{
return 1 + _strlen_(s+1);
}
else
{
return 0;
}
}或
unsigned int _strlen_(const char* s)
{
return s ? (*s ? (1 + _strlen_(s+1)) : 0) : 0;
}2.递归的应用
2.1 单向链表的转置
预备的单链表：
#include
using namespace std;
struct Node
{
int value;
Node* next;
};
Node* create_list(int v, int len)
{
Node* ret = NULL;
Node* slider = NULL;
for(int i=0; ivalue = v++;
n->next = NULL;
if( slider == NULL )
{
slider = n;
ret = n;
}
else
{
slider->next = n;
slider = n;
}
}
return ret;
}
void destroy_list(Node* list)
{
while( list )
{
Node* del = list;
list = list->next;
delete del;
}
}
void print_list(Node* list)
{
while( list )
{
cout << list->value << "->";
list = list->next;
}
cout << "NULL" << endl;
}
int main()
{
Node* list = create_list(1, 5);
print_list(list);
destroy_list(list);
return 0;
} 运行结果为：
1->2->3->4->5->NULL单向链表的转置：
Node* reverse(Node* list)
{
if( (list == NULL) || (list->next == NULL) )
{
return list;
}
else
{
Node* guard = list->next;
Node* ret = reverse(list->next);
guard->next = list;
list->next = NULL;
return ret;
}
}
int main()
{
Node* list = create_list(1, 5);
print_list(list);
list = reverse(list);
print_list(list);
destroy_list(list);
return 0;
}运行结果为：
1->2->3->4->5->NULL
5->4->3->2->1->NULL2.2 单向排序链表的合并
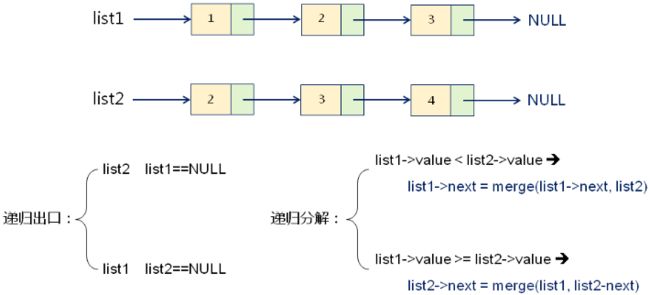
单向排序链表的合并：
Node* merge(Node* list1, Node* list2)
{
if( list1 == NULL )
{
return list2;
}
else if( list2 == NULL )
{
return list1;
}
else if( list1->value < list2->value )
{
Node* list_1 = list1->next;
Node* list = merge(list_1, list2);
list1->next = list;
return list1;
}
else
{
Node* list_2 = list2->next;
Node* list = merge(list1, list_2);
list2->next = list;
return list2;
}
}
int main()
{
Node* list1 = create_list(1, 5);
Node* list2 = create_list(2, 6);
print_list(list1);
print_list(list2);
Node* list = merge(list1, list2);
print_list(list);
destroy_list(list);
return 0;
}运行结果为：
1->2->3->4->5->NULL
2->3->4->5->6->7->NULL
1->2->2->3->3->4->4->5->5->6->7->NULL代码优化：
Node* merge(Node* list1, Node* list2)
{
if( list1 == NULL )
{
return list2;
}
else if( list2 == NULL )
{
return list1;
}
else if( list1->value < list2->value )
{
return (list1->next = merge(list1->next, list2), list1);
}
else
{
return (list2->next = merge(list1, list2->next), list2);
}
}2.3 汉诺塔问题
汉诺塔问题：
- 将木块借助 B 柱由 A 柱移动到 C 柱
- 每次只能移动一个木块
- 只能出现小木块在大木块之上
汉诺塔问题分解：
- 将 n-1 个木块借助 C 柱由 A 柱移动到 B 柱
- 将最底层的唯一木块直接移动到 C 柱
- 将 n-1 个木块借助 A 柱由 B 柱移动到 C 柱
汉诺塔问题：
void HanoiTower(int n, char a, char b, char c) // a ==> src, b ==> middle, c ==> dest
{
if( n == 1 )
{
cout << a << "-->" << c << endl;
}
else
{
HanoiTower(n-1, a, c, b);
HanoiTower(1, a, b, c);
HanoiTower(n-1, b, a, c);
}
}
int main()
{
HanoiTower(3, 'a' ,'b', 'c');
return 0;
}运行结果为：
a-->c
a-->b
c-->b
a-->c
b-->a
b-->c
a-->c2.4 全排列问题
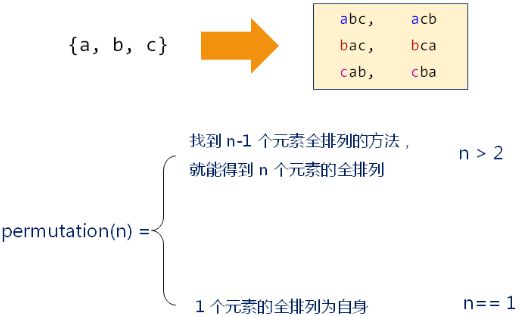
全排列问题：
void permutation(char* s, char* e) // e始终指向字符数组的首元素
{
if( *s == '\0' )
{
cout << e << endl;
}
else
{
int len = strlen(s);
for(int i=0; i运行结果为：
abc
acb
bac
bca
cba
cab但是如果存在相同的元素，则会有重复结果，例如：
int main()
{
char s[] = "aac";
permutation(s, s);
return 0;
}运行结果为：
aac
aca
aac
aca
caa
caa代码优化：
void permutation(char* s, char* e) // e始终指向字符数组的首元素
{
if( *s == '\0' )
{
cout << e << endl;
}
else
{
int len = strlen(s);
char mark[256] = {0};
for(int i=0; i运行结果为：
aac
aca
caa2.5 逆序打印单链表中的偶数结点
递归还能用于需要回溯穷举的场合。。。
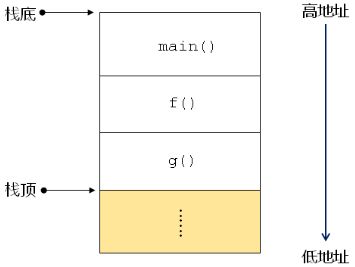
函数调用过程回顾：
- 程序运行后有一个特殊的内存区供函数调用使用
- 用于保存函数中的实参，局部变量，临时变量，等
- 从起始地址开始往一个方向增长 ( 如 : 高地址 → 低地址 )
- 有一个专用“指针”标识当前已使用内存的“顶部”
程序中的栈区：一段特殊的专用内存区
实例分析：逆序打印单链表中的偶数结点
逆序打印单链表中的偶数结点：
void r_print_even(Node* list)
{
if( list != NULL )
{
r_print_even(list->next);
if( (list->value % 2) == 0 )
{
cout << list->value << endl;
}
}
}
int main()
{
Node* list = create_list(2, 5);
print_list(list);
r_print_even(list);
destroy_list(list);
return 0;
}运行结果为：
2->3->4->5->6->NULL
6
4
22.6 八皇后问题
八皇后问题：
- 在一个8x8的国际象棋棋盘上，有8个皇后，每个皇后占一格；要求皇后间不会出现相互“攻击”的现象 ( 不能有两个皇后处在同一行、同一列或同一对角线上 )。
关键数据结构定义：
- 棋盘：二维数组 ( 10 * 10 )
- 0 表示位置为空，1 表示皇后，2 表示边界
- 位置：struct Pos;
- 方向：
算法思路：
八皇后问题：
#include
#include "LinkList.h"
using namespace std;
using namespace StLib;
template
class QueueSolution : public Object
{
protected:
enum { N = SIZE + 2 };
struct Pos : public Object
{
Pos(int px = 0, int py = 0) : x(px), y(py) { }
int x;
int y;
};
int m_chessboard[N][N];
Pos m_direction[3];
LinkList m_solution;
int m_count;
void init()
{
m_count = 0;
for(int i=0; i qs;
qs.run();
return 0;
} 测试四皇后问题的运行结果为：
(2, 1) (4, 2) (1, 3) (3, 4)
******
* # *
*# *
* #*
* # *
******
(3, 1) (1, 2) (4, 3) (2, 4)
******
* # *
* #*
*# *
* # *
******
Total: 2（八皇后问题一共有92个解。）
3.小结
- 递归是一种将问题分而自治的思想
- 用递归解决问题首先要建立递归的模型
- 递归解法必须要有边界条件，否则无解
- 不要陷入递归函数的执行细节，学会通过代码描述递归问题
- 程序运行后的栈存储区专供函数调用使用
- 栈存储区用于保存实参，局部变量，临时变量，等
- 利用栈存储区能够方便的实现回溯算法
- 八皇后问题是栈回溯的经典应用