MADlib——基于SQL的数据挖掘解决方案（21）——分类之KNN

一、分类方法概要

 

1.  分类的概念

        数据挖掘中分类的目的是学会一个分类函数或分类模型，该模型能把数据库中的数据项映射到给定类别中的某一个。分类可描述如下：输入数据，或称训练集（Training Set），是由一条条数据库记录（Record）组成的。每一条记录包含若干个属性（Attribute），组成一个特征向量。训练集的每条记录还有一个特定的类标签（Class Label）与之对应。该类标签是系统的输入，通常是以往的一些经验数据。一个具体样本的形式可为样本向量：(v1,v2,...,vn;c)，在这里vi表示字段值，c表示类别。分类的目的是：分析输入数据，通过在训练集中的数据表现出来的特征，为每一个类找到一种准确的描述或模型。由此生成的类描述用来对未来的测试数据进行分类。尽管这些测试数据的类标签是未知的，我们仍可以由此预测这些新数据所属的类。注意是预测，而不是肯定，因为分类的准确率不能达到百分之百。我们也可以由此对数据中的每一个类有更好的理解。也就是说：我们获得了对这个类的知识。

        所以分类（Classification）也可以定义为：对现有的数据进行学习，得到一个目标函数或规则，把每个属性集 x 映射到一个预先定义的类标号 y。目标函数或规则也叫分类模型（Classification Model），它有两个主要作用：一是描述性建模，即作为解释性工具，用于区分不同类的对象；二是预测性建模，即用于预测未知记录的类标号。

 

2.  分类的原理

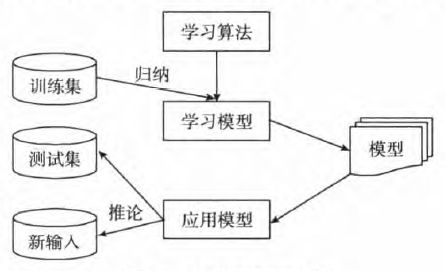
        分类方法是一种根据输入数据建立分类模型的系统方法，这些方法都是使用一种学习算法（Learning Algorithm）确定分类模型，使该模型能够很好地拟合输入数据中类标号和属性集之间的联系。学习算法得到的模型不仅要很好地拟合输入数据，还要能够正确地预测未知样本的类标号。因此，训练算法的主要目标就是建立具有很好泛化能力的模型，即建立能够准确预测未知样本类标号的模型。图1展示了解决分类问题的一般方法。首先，需要一个训练集，它由类标号已知的记录组成。使用训练集建立分类模型，该模型随后将运用于检验集（Test Set），检验集由类标号未知的记录组成。

图1 分类原理示意图

        

        通常分类学习所获得的模型可以表示为分类规则形式、决策树形式或数学公式形式。例如，给定一个顾客信用信息数据库，通过学习所获得的分类规则可用于识别顾客是否具有良好的信用等级或一般的信用等级。分类规则也可用于对今后未知所属类别的数据进行识别判断，同时还可以帮助了解数据库中的内容。

        构造模型的过程一般分为训练和测试两个阶段。在构造模型之前，要求将数据集随机地分为训练数据集和测试数据集。在训练阶段，使用训练数据集，通过分析由属性描述的数据库元组来构造模型，假定每个元组属于一个预定义的类，由一个称作类标号的属性来确定。训练数据集中的单个元组也称作训练样本。由于提供了每个训练样本的类标号，该阶段也被称为有指导的学习。在测试阶段，使用测试数据集来评估模型的分类准确率，如果认为模型的准确率可以接受，就可以用该模型对其它数据元组进行分类。一般来说，测试阶段的代价远远低于训练阶段。

        为了提高分类的准确性、有效性和可伸缩性，在进行分类之前，通常要对数据进行预处理，包括：

        1）数据清理。其目的是消除或减少数据噪声，处理空缺值。

        2）相关性分析。由于数据集中的许多属性可能与分类任务不相关，若包含这些属性可能会减慢或误导学习过程。相关性分析的目的就是删除这些不相关或冗余的属性。

        3）数据变换。数据可以概化到较高层概念。比如，连续值属性“收入”的数值可以概化为离散值：低、中、高。又比如，标称值属性“市”可以概化到高层概念“省”。此外，数据也可以规范化，规范化将给定属性的值按比例缩放，落入较小的区间，比如[0,1]等。

  

二、K近邻简介

1.  KNN原理

        K近邻（K-Nearest Neighbor，KNN）算法是一种基于实例的分类方法，最初由Cover和Hart于1968年提出，是一种非参数的分类技术。非参数方法推迟对训练数据的建模，只需要假定一个事实，即相似的输入具有相似的输出。

        K近邻分类方法通过计算每个训练样例到待分类样品的距离，取和待分类样品距离最近的K个训练样例，K个样品中哪个类别的训练样例占多数，则待分类元组就属于哪个类别。使用最近邻确定类别的合理性可用下面的谚语来说明：“如果走像鸭子，叫像鸭子，看起来还像鸭子，那么它很可能就是一只鸭子”。最近邻分类器把每个样例看作d维空间上的一个数据点，其中d是属性个数。给定一个测试样例，我们可以计算该测试样例与训练集中其它数据点的距离（邻近度），给定样例z的K最近邻是指找出和z距离最近的K个数据点。

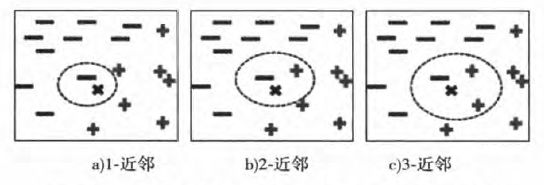
        图2给出了位于圆圈中心的数据点的1-最近邻、2-最近邻和3-最近邻。该数据点根据其近邻的类标号进行分类。如果数据点的近邻中含有多个类标号，则将该数据点指派到其最近邻的多数类。在图2a中，数据点的1-最近邻是一个负例，因此该点被指派到负类。如果最近邻是三个，如图2c所示，其中包括两个正例和一个负例，根据多数表决方案，该点被指派到正类。在最近邻中正例和负例个数相同的情况下（见图2b），可随机选择一个类标号来分类该点。

图2 一个实例的1-最近邻、2-最近邻、3-最近邻

        

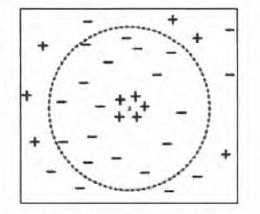
        前面讨论中强调了选择合适K值的重要性。如果K太小，则最近邻分类器容易受到由于训练数据中的噪声而产生的过分拟合的影响；相反，如果K太大，最近邻分类器可能会误分类测试样例，因为最近邻列表中可能包含远离其近邻的数据点（见图3）。推定K值的有益途径是通过有效参数的数目这个概念。有效参数的数目是和K值相关的，大致等于n/K，n是这个训练集中实例的数目。在实践中往往通过若干次实验来确定K值，取分类误差率最小的K值。

图3 K较大时的K-最近邻分类

 

2.  KNN算法

        下面是对最近邻分类方法的一个高层描述。

 

1：令K是最近邻数目，D是训练样例的集合

2：for 每个测试样例 do

3：        计算z和每个样例 之间的距离

4：        选择离z最近的K个训练样例的集合

5：         

6：end for

 

        对每一个测试样例  ，算法计算它和所有训练样例  之间的距离（或相似度），以确定其最近邻列表  。如果训练样例的数目很大，那么这种计算的开销就会很大。然而，高效的索引技术可以降低为测试样例找最近邻时的计算量。

        一旦得到最近邻列表，测试样例就会根据最近邻中的多数类进行分类：

 多数表决：

 

        其中，  是类标号，  是一个最近邻的类标号，  是指示函数，如果其参数为真，则返回1，否则返回0。

        在多数表决方法中，每个近邻对分类的影响都一样，这使得算法对K的选择很敏感，如图2所示。降低K的影响的一种途径是根据最近邻  距离的不同对其作用加权： 。结果使得远离z的训练样例对分类的影响要比那些靠近z的训练样例弱一些。使用距离加权表决方案，类标号可以由下面的公式确定：

距离加权表决：

 

        考虑表1中的一维数据集，根据1-最近邻、3-最近邻、5-最近邻及9-最近邻，对数据点x=0.5的分类结果分别是+、-、+、-，但如果使用距离加权表决方法，则x=5.0的分类结果分别是+、+、+、+。

x	0.5	3.0	4.5	4.6	4.9	5.2	5.3	5.5	7.0	9.5
y	-	-	+	+	+	-	-	+	-	-
d	4.5	2.0	0.5	0.4	0.1	0.2	0.3	0.5	2.0	4.5
w	0.05	0.25	4	6.25	100	24.5	11.11	4	0.25	0.05

表1 一维数据集的距离加权

 

3.  KNN特征

        最近邻分类器的特点总结如下：

• 最近邻分类属于一类广泛的技术，这种技术称为基于实例的学习，它使用具体的训练实例进行预测，而不必维护源自数据的抽象（或模型）。基于实例的学习算法需要邻近性度量来确定实例间的相似性或距离，还需要分类函数根据测试实例与其它实例的邻近性返回测试的预测类标号。
• 像最近邻分类器这样的学习方法不需要建立模型，然而，分类测试样例的开销很大，因为需要逐个计算测试样例和训练样例之间的相似度。相反，参数化的学习方法通常花费大量计算资源建立模型，模型一旦建立，分类测试样例就会很快。
• 最近邻分类器基于局部信息进行预测，因此当K很小时对噪声非常敏感。
• 最近邻分类器可以生成任意形状边界的决策边缘，能提供更加灵活的模型表示。最近邻分类器的局侧边缘还有很高的可变性，因为它们依赖于训练样例的组合。增加最近邻数目可以降低这种可变性。
• 除非采用适当的邻近性度量和数据预处理，否则最近邻分类器可能做出错误的预测。例如，我们想根据身高（以米为单位）和体重（以斤为单位）等属性对一群人分类。高度的可变性很小，从1.5米到1.85米，而体重范围则可能从90斤到200斤。如果不考虑属性值的单位，那么邻近性度量可能就会被人的体重差异所左右。

 

二、MADlib中KNN函数

        MADlib提供的KNN函数仍然处于早期开发阶段。将来的版本会解决一些问题，并且接口和实现可能会发生变化。正如前面所讨论的，MADlib的KNN函数以训练数据集作为输入数据点，训练数据集中包含测试样例中的特征，函数在训练集中为测试集中的每个数据点查找K个最近点。KNN函数的输出取决于任务类型。对于分类，输出是K个最近数据点类别的多数票对应的类别。也就是说，测试样例被分配给了最近邻中最可能的类。而对于回归，输出是给定测试点K个最近邻的平均值。

 

1. 语法

knn( point_source,
     point_column_name,
     label_column_name,
     test_source,
     test_column_name,
     id_column_name,
     output_table,
     operation,
     k
   )

 

2. 参数

参数名称	数据类型	描述
point_source	TEXT	包含训练数据点的表的名称。训练数据点应该按行存储在类型为DOUBLE PRECISION[]的列中。
point_column_name	TEXT	包含训练数据点的列名。
label_column_name	TEXT	具有训练数据点类标签的列名。
test_source	TEXT	包含测试数据点的表的名称。测试数据点应该按行存储在类型为DOUBLE PRECISION[]的列中。
test_column_name	TEXT	包含训练数据点的列名。
id_column_name	TEXT	测试数据表中具有数据点ID的列的名称。
output_table	TEXT	存储输出结果的表名。
operation	TEXT	任务类型：‘r’表示回归，‘c’表示分类。
K（可选）	INTEGER	缺省值为1，最近邻数量。对于分类，应该是一个奇数。

表2 knn函数参数说明

3. 输出

        KNN函数的输出是一个包含以下列的表：

        id：INTEGER类型，测试数据点的ID。

        test_column_name：DOUBLE PRECISION[]类型，测试数据点。

        prediction：INTEGER类型，类别标签或回归的均值。

 

三、示例

        本示例取自维基百科中的“决策树”条目，问题描述如下：

        小王是一家著名高尔夫俱乐部的经理。但是他被雇员数量问题搞得心情十分不好。某些天好像所有人都來玩高尔夫，以至于所有员工都忙的团团转还是应付不过来，而有些天不知道什么原因却一个人也不来，俱乐部为雇员数量浪费了不少资金。小王的目的是通过下周天气预报寻找什么时候人们会打高尔夫，以适时调整雇员数量。因此首先他必须了解人们决定是否打球的原因。在两周时间内可以得到以下记录：天气状况有晴、云和雨；华氏温度表示的气温；相对湿度百分比；是否有风。当然还有顾客是不是在这些日子光顾俱乐部。最终他得到了表3所示的14行5列的数据。

自变量				因变量
天气情况	华氏温度	相对湿度	是否有风	是否打球
sunny	85	85	FALSE	Don’t Play
sunny	80	90	TRUE	Don’t Play
overcast	83	78	FALSE	Play
rain	70	96	FALSE	Play
rain	68	80	FALSE	Play
rain	65	70	TRUE	Don’t Play
overcast	64	65	TRUE	Play
sunny	72	95	FALSE	Don’t Play
sunny	69	70	FALSE	Play
rain	75	80	FALSE	Play
sunny	75	70	TRUE	Play
overcast	72	90	TRUE	Play
overcast	81	75	FALSE	Play
rain	71	80	TRUE	Don’t Play

表3 两周天气与是否打高尔夫球数据

        我们将利用MADlib的KNN函数来解决此问题。

 1.  准备训练数据

        将天气、温度、湿度数据进行0-1标准化，去除数据的单位限制，将其转化为无量纲的纯数值，便于不同单位或量级的指标能够进行比较和加权。

drop table if exists source_data;
create table source_data (c1 int, c2 int, c3 int, c4 int, c5 int, c6 int);
insert into source_data values 
(1, 1,85,85,0, 0),
(2, 1,80,90,1, 0),
(3, 2,83,78,0, 1),
(4, 3,70,96,0, 1),
(5, 3,68,80,0, 1),
(6, 3,65,70,1, 0),
(7, 2,64,65,1, 1),
(8, 1,72,95,0, 0),
(9, 1,69,70,0, 1),
(10,3,75,80,0, 1),
(11,1,75,70,1, 1),
(12,2,72,90,1, 1),
(13,2,81,75,0, 1),
(14,3,71,80,1, 0);

drop table if exists knn_train_data;
create table knn_train_data (
                    id integer, 
                    data float8[], 
                    label integer
                    );

insert into knn_train_data 
select c1, 
       array[round((c2 - min_c2)/cast((max_c2 - min_c2) as numeric),4)::float8,
             round((c3 - min_c3)/cast((max_c3 - min_c3) as numeric),4)::float8,
             round((c4 - min_c4)/cast((max_c4 - min_c4) as numeric),4)::float8,
             c5],
       c6
  from source_data,
       (select min(c2) min_c2,max(c2) max_c2,
               min(c3) min_c3,max(c3) max_c3,
   min(c4) min_c4,max(c4) max_c4 
      from source_data) t;

2.  准备测试数据

        用平均温度和湿度测试。   

select round((avg(c3)-min(c3))/(max(c3)-min(c3)),4),
       round((avg(c4)-min(c4))/(max(c4)-min(c4)),4)
  from source_data;

        结果：

 round  | round  
--------+--------
 0.4558 | 0.4931
(1 row)

        生成测试数据。

drop table if exists knn_test_data;
create table knn_test_data 
( id integer, 
  data float8[]
);

insert into knn_test_data values
(1, '{0,0.4558,0.4931,0}'),
(2, '{0.5,0.4558,0.4931,0}'),
(3, '{1,0.4558,0.4931,0}'),
(4, '{0,0.4558,0.4931,1}'),
(5, '{0.5,0.4558,0.4931,1}'),
(6, '{1,0.4558,0.4931,1}');

 

3.  运行KNN分类

drop table if exists madlib_knn_result_classification;
select * from madlib.knn( 
                'knn_train_data',      -- 训练数据表
                'data',                -- 训练数据列
                'label',               -- 类别标签列
                'knn_test_data',       -- 测试数据表
                'data',                -- 测试数据列
                'id',                  -- 测试数据ID列 
                'madlib_knn_result_classification',  -- 输出表
                'c',                   -- 分类
                 1                     -- 最近邻数
                );

 

4.  查看输出结果

select * from madlib_knn_result_classification order by id;

        结果：

 id |         data          | prediction 
----+-----------------------+------------
  1 | {0,0.4558,0.4931,0}   |          1
  2 | {0.5,0.4558,0.4931,0} |          1
  3 | {1,0.4558,0.4931,0}   |          1
  4 | {0,0.4558,0.4931,1}   |          1
  5 | {0.5,0.4558,0.4931,1} |          1
  6 | {1,0.4558,0.4931,1}   |          0
(6 rows)