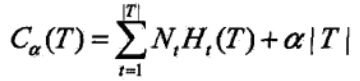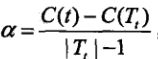决策树原理简介

基于决策树（DT）的算法如RF、GBDT在各种工业场景有着广泛的应用，了解决策树基础算法非常重要，下面我们就对于决策树算法做一下总结

决策树分类器基本思想

决策树是一种基于分治法的分类器。假设我们有若干个样本点，把它们放在一个节点内，按照最原始的方法对数据做分类，我们可以对节点内部的样本标签做统计，每一个新的样本都可以归为标签的众数（数量最多的标签）；当然，这个方法太粗暴没有实用价值，那么我们是否可以通过某种规则将这个节点内的样本点分成若干个子节点，在小节点上运用同样的众数方法判断分类。可以确定的是，如果规则选择的好，分类准确度是一定可以提高的。按照这个方向，子节点仍然可以衍生出其本身的子节点以提供分类准确度。

决策树算法

（1）决策树的生成

决策树节点的分支规则是怎样的呢？通常它是围绕着节点样本的某一个特征展开的：我么首先会选择节点样本的某个特征，以该特征为基础将样本分成若干个分支。

我们假设样本特征都是离散特征（对于连续特征后面会讲），那么分支的过程即为特征选择的过程：只要选定了特征，随即依照不同的特征值类别将父节点的样本分配给子节点。特征的选择应该按照什么原则？我们可以从信息的角度来分析分类问题，如果一个节点的分类效果好，那么它内部样本的类别分布应该是比较单一而非混杂的，或者说从系统上说，它的熵是比较小的，反之则比较大。回忆互信息的定义，一种理解方式即给定事件A可以在多大程度上降低D的不确定性，如果我们将A定义为选定了某一个特征，D定义为样本的分类，那么的大小恰好就可以衡量分支的好坏：越大熵降低的越多，这是我们希望看到的，反之越少。

这样，我们可以使用互信息来选择不同的特征，当然这里和是“经验”熵。设C代表类别，熵的计算公式如下：

                                                                      

                                                           

事实上，上述方法有一个隐患，取值比较多的特征比取值少的特征互信息大，同等条件下总是选择取值比较多的特征显然是不合理的，因此一种改进的做法是使用信息增益比：

                                                                              

来代替互信息做判断。

有了单个节点分支的策略，接下来就是要递归地重复这个过程，直到节点内部只有一个单一的类别。

（2）决策树的剪枝

由上述方式生成的决策树虽然在训练数据上有着很好的表现，但是泛化能力却很差。为了解决这个问题，我们要使用剪枝策略。决策树的剪枝通过极小化决策树的损失函数来实现，设树T的叶节点个数为|T|，t是树T的叶节点，该叶节点有个样本点，其中k类的样本点有个，类别总共有K个，则损失函数可以表示为：

                                                                  

可以看到，过多的叶节点的会使得损失函数增大。这和我们建立机器学习模型的经验是相吻合的，越复杂的模型往往容易发生过拟合。

要使得损失函数最小化，全局搜索是比较困难的，为此我们使用启发式的树的剪枝算法：

 

（3）CART树算法

CART树作为一种改进的决策树，其结构简单，计算速度快，在工业上得到了广泛的应用。CART树与C4.5和ID3决策树有多处不同。

1. 计算互信息时由于有log运算，所以计算速度比较慢，CART改进了这一点，使用gini指数而非互信息运算来表示不纯度。

gini指数定义如下：

2. CART树是二叉树，每个父节点只能生成两个分支。

如果特征是离散值，我们循环访问该特征的每个属性，对于每一个属性，我们计算按此属性做二类划分所能得到的gini值，选取最小的那个作为划分条件。如果特征是连续值，我们取每两个样本的中间值所谓候选划分点，以小于或者大于该划分点计算gini值，同样先去最小的作为划分条件。

3. CART树剪枝策略很不一样。

预剪枝这里就不说，包括对于深度的限制，节点样本数据大小的限制。这里讲一下CART的后剪枝策略。我们知道对于决策树的任意一个子树T，我们都可以计算其损失函数：

                                                                   

其中C(T)是对于子树对于属于其样本的训练数据误差，|T|是子树叶节点个数。设子树T的根节点是t，其剪枝后的损失函数为：

                                                                      

我们知道，随着的增大，最优子树的叶节点会越来越少；那么当大到一定程度，T就需要做完全剪枝，即只留下一个根节点t。该为：

                                                                      

我们将其称作为误差增益。对于整个决策树，我们对每一个节点都可以求其对应的误差增益；逐渐增加误差增益，将低于该的子树剪掉，这样我们就可以得到一系列的决策树。最后用测试数据较差验证选择最优的子树就好。

决策树处理缺失值

对于决策树，我们需要考虑3种缺失值的情况。

1. 在选择特征作为分支依据时，某个样本的特征值缺失。对于这种情况，我们会忽略吗该样本来计算最终信息增益，不过最后结果要做加权。比如，节点有10个样本，在计算特征a时发现样本s1的特征a是缺失的，则我们计算信息增益时候跳过s1的到结果0.9，但是我们是用10个样本中的9个得到该结果的，所以结果要再乘以9/10，信息增益就是0.9*0.9=0.81。

2. 分支时特征已经选好，但是分配样本时有样本该特征缺失。遇到该情况，该样本可以同时分配到不同的分支，但权重并非为1而是特征不同属性值所占的比例

3. 测试数据特征值缺失。这种情况处理的方法就比较多了，其中一种是为样本特征设置一个值，这个值为样本中该特征出现次数最多的属性。

总结

我们来看一下决策树模型的又优缺点。

优点：

1. 易于理解， 树容易可视化

2. 不需要白化数据；缺失值不需要提前做特殊处理；

3. 连续以及离散数据都可以处理

缺点：

1. 对少量数据很敏感，少量数据上的变动可能差生完全不同的决策树，这一点也可以解释为容易过拟合。可以通过bagging和boosting的方法来改善。

2. 学习一个最优的决策树是NP难度问题（类似CART树的剪枝策略是启发式方法，并非全局最优），这同样可以通过融合的方法来改善。

3. 有些概念决策树不易学到（也就是虽然其为非线性模型，但其表达能力也是有限的），比如XOR关系。

4. 决策树在处理回归问题时，对于其没有遇到过的类型的数据，缺乏泛化能力