500行C++代码实现软件渲染器 - 2.三角形光栅化与背面剔除

填充三角形

大家好，这是我。

更精确来讲，这是用接下来一两个小时内我们将创建的程序渲染出来的我的脸的模型。上一次，我们绘制了三维模型的线框。这一次，我们将填充多边形，或者三角形。事实上，OpenGL几乎会对所有的多边形进行三角化，所以这里我们不需要去考虑更复杂的情况。

需要提醒的是，本系列教程设计的目的是帮助你自己独立编程。当我说你可以在两个小时内绘制一个类似上面的图像，我并不是说阅读代码的时间，而是从零开始编码的时间。我提供的代码只是为了给你一个参照。我不是一个优秀的程序员，极有可能你比我优秀，所有不要复制粘贴我的代码。欢迎任何评论和咨询。

老派方法：扫描线算法

因此，我们的任务是绘制二维三角形。对于积极性比较强的学生，这大概花费几个小时，即便他们是比较差的程序员，上一次，我们看到了Bresenham的直线算法。今天我们的任务是绘制填充三角形。虽然有点搞笑，但是这个任务不是无意义的。我不知道为什么，但是我知道这是对的。我的大部分学生会在这个简单的问题上挣扎。所以，初始代码将是这样的：

void triangle(Vec2i t0, Vec2i t1, Vec2i t2, TGAImage &image, TGAColor color) { 
    line(t0, t1, image, color); 
    line(t1, t2, image, color); 
    line(t2, t0, image, color); 
}

// ...

Vec2i t0[3] = {Vec2i(10, 70),   Vec2i(50, 160),  Vec2i(70, 80)}; 
Vec2i t1[3] = {Vec2i(180, 50),  Vec2i(150, 1),   Vec2i(70, 180)}; 
Vec2i t2[3] = {Vec2i(180, 150), Vec2i(120, 160), Vec2i(130, 180)}; 
triangle(t0[0], t0[1], t0[2], image, red); 
triangle(t1[0], t1[1], t1[2], image, white); 
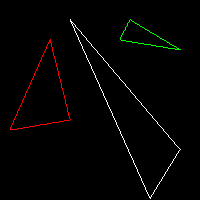
triangle(t2[0], t2[1], t2[2], image, green);

同往常一样，代码提交到了Github。代码很简单。我提供了三个三角形供你调试使用。如果我们调用三角形函数内的line()，我们将得到三角形的外轮廓。那么怎么绘制一个填充的三角形呢？

一个比较好的绘制算法必须具有以下特点：

• 它必须简单且高效
• 它必须是对称的，也就是说绘制的结果不应该依赖于顶点传入的顺序
• 如果两个三角形具有相同的顶点，那么考虑到光栅化的完整性，三角形之间不能有空隙
• 我们可以增加更多的要求，但是我们先增加一个：通常使用扫描线算法

1. 将三角形顶点根据y坐标排序
2. 同时光栅化三角形的左边和右边
3. 在左右边界点之间绘制一条水平线段

在这个时候，我的学生开始产生疑问了：哪个线段是左边，哪个是右边？三角形里面有三个线段啊？通常，介绍完之后，我会给我的学生一个小时写代码。再次声明，直接阅读我的代码与将我的代码和自己的代码比较相比是更没有价值的。

【一个小时过去了】

怎样绘制三角形呢？如果你有一个更好的额办吧，我很乐意使用它。当我们假设三角形有三个顶点：t0、t1、t2，它们按照y坐标递增的顺序排列。然后，边界A由t0和t2相连，边界B由t0和t1相连、t1和t2相连两部分组成。

void triangle(Vec2i t0, Vec2i t1, Vec2i t2, TGAImage &image, TGAColor color) { 
    // sort the vertices, t0, t1, t2 lower−to−upper (bubblesort yay!) 
    if (t0.y>t1.y) std::swap(t0, t1); 
    if (t0.y>t2.y) std::swap(t0, t2); 
    if (t1.y>t2.y) std::swap(t1, t2); 
    line(t0, t1, image, green); 
    line(t1, t2, image, green); 
    line(t2, t0, image, red); 
}

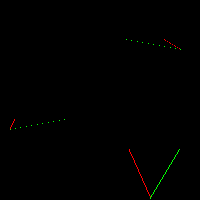
在这里边界A为红色，边界B为绿色。

不行的是，边界B由两部分组成，让我们沿水平切断，只绘制下半部分。

void triangle(Vec2i t0, Vec2i t1, Vec2i t2, TGAImage &image, TGAColor color) { 
    // sort the vertices, t0, t1, t2 lower−to−upper (bubblesort yay!) 
    if (t0.y>t1.y) std::swap(t0, t1); 
    if (t0.y>t2.y) std::swap(t0, t2); 
    if (t1.y>t2.y) std::swap(t1, t2); 
    int total_height = t2.y-t0.y; 
    for (int y=t0.y; y<=t1.y; y++) { 
        int segment_height = t1.y-t0.y+1; 
        float alpha = (float)(y-t0.y)/total_height; 
        float beta  = (float)(y-t0.y)/segment_height; // be careful with divisions by zero 
        Vec2i A = t0 + (t2-t0)*alpha; 
        Vec2i B = t0 + (t1-t0)*beta; 
        image.set(A.x, y, red); 
        image.set(B.x, y, green); 
    } 
}

注意，线段并不是连续的。上一次，我们绘制的直线的时候，我们费了一番周折才绘制出连续的直线。在这里，我们暂时不用对图像进行翻转（还记得xy左边的交换吗？）。为什么呢，因为我们可以直接对三角形进行填充，这就是理由。我们我们沿水平方向将相应的点连接起来，缺口就消失了。

现在，让我们绘制上半部分三角形，我们可以再增加一个循环体。

void triangle(Vec2i t0, Vec2i t1, Vec2i t2, TGAImage &image, TGAColor color) { 
    // sort the vertices, t0, t1, t2 lower−to−upper (bubblesort yay!) 
    if (t0.y>t1.y) std::swap(t0, t1); 
    if (t0.y>t2.y) std::swap(t0, t2); 
    if (t1.y>t2.y) std::swap(t1, t2); 
    int total_height = t2.y-t0.y; 
    for (int y=t0.y; y<=t1.y; y++) { 
        int segment_height = t1.y-t0.y+1; 
        float alpha = (float)(y-t0.y)/total_height; 
        float beta  = (float)(y-t0.y)/segment_height; // be careful with divisions by zero 
        Vec2i A = t0 + (t2-t0)*alpha; 
        Vec2i B = t0 + (t1-t0)*beta; 
        if (A.x>B.x) std::swap(A, B); 
        for (int j=A.x; j<=B.x; j++) { 
            image.set(j, y, color); // attention, due to int casts t0.y+i != A.y 
        } 
    } 
    for (int y=t1.y; y<=t2.y; y++) { 
        int segment_height =  t2.y-t1.y+1; 
        float alpha = (float)(y-t0.y)/total_height; 
        float beta  = (float)(y-t1.y)/segment_height; // be careful with divisions by zero 
        Vec2i A = t0 + (t2-t0)*alpha; 
        Vec2i B = t1 + (t2-t1)*beta; 
        if (A.x>B.x) std::swap(A, B); 
        for (int j=A.x; j<=B.x; j++) { 
            image.set(j, y, color); // attention, due to int casts t0.y+i != A.y 
        } 
    } 
}

这个效果可能就够了，但是我不喜欢重复的代码。虽然这会让代码可读性变差，但是也会为修改和维护提供更多便利。

void triangle(Vec2i t0, Vec2i t1, Vec2i t2, TGAImage &image, TGAColor color) { 
    if (t0.y==t1.y && t0.y==t2.y) return; // I dont care about degenerate triangles 
    // sort the vertices, t0, t1, t2 lower−to−upper (bubblesort yay!) 
    if (t0.y>t1.y) std::swap(t0, t1); 
    if (t0.y>t2.y) std::swap(t0, t2); 
    if (t1.y>t2.y) std::swap(t1, t2); 
    int total_height = t2.y-t0.y; 
    for (int i=0; it1.y-t0.y || t1.y==t0.y; 
        int segment_height = second_half ? t2.y-t1.y : t1.y-t0.y; 
        float alpha = (float)i/total_height; 
        float beta  = (float)(i-(second_half ? t1.y-t0.y : 0))/segment_height; // be careful: with above conditions no division by zero here 
        Vec2i A =               t0 + (t2-t0)*alpha; 
        Vec2i B = second_half ? t1 + (t2-t1)*beta : t0 + (t1-t0)*beta; 
        if (A.x>B.x) std::swap(A, B); 
        for (int j=A.x; j<=B.x; j++) { 
            image.set(j, t0.y+i, color); // attention, due to int casts t0.y+i != A.y 
        } 
    } 
}

这里是绘制二维三角形的代码。

我所使用的方法

扫描线算法虽然不复杂，但是代码还是有点乱。同时，它也是为单线程编程所设计的老派方法。让我们先看一下以下伪代码：

triangle(vec2 points[3]) { 
    vec2 bbox[2] = find_bounding_box(points); 
    for (each pixel in the bounding box) { 
        if (inside(points, pixel)) { 
            put_pixel(pixel); 
        } 
    } 
}

你喜欢这个代码吗？反正我很喜欢。要找到包围盒很容易，要检查一个点是否在二维三角形内部或者任意凸多边形内部也是没问题的。

题外话：如果我要实现一个算法来判断点是否在多边形内，并且这个程序在飞机上运行，那么我绝不会坐这个飞机。事实证明，要可靠的解决这个问题是非常困难的。但是在这里，我们只是绘制要素，就没关系了。

关于这段伪代码还有一点我比较喜欢的是，编程新手很乐意接受它，而有经验的程序员会呛道：“哪个蠢货写的代码”，但是图形学专家会耸耸肩膀说：“实际上真实世界里程序就是这么工作的”。成千上万个线程中的大规模并行计算（我在这里谈论的是常规消费级计算机）改变了思维方式。

好的，让我们开始：首先，我们需要知道什么是重心坐标系。给定一个二维三角形ABC和一个点P，所有的点都是以笛卡尔坐标系(x,y)给出。我们的目标是找到点P相对于三角形ABC的重心坐标。这意味着，我们需要找到三个数字（1  -  u  -  v，u，v），使P满足如下：

咋一看有些害怕，实际却很简单。想象以下，我们把三个权重（1  -  u  -  v，u，v）相应的赋给点A、B和C。那么系统的中心刚好在P点。或者我们可以说：

我们有向量，和，我们要找到两个实数u和v，满足：

这是一个简单的向量方程，或者说是两个二元一次方程。

我很懒，不想以学者的方式解线性方程。让我们用矩阵的方式重写一下：

也就是说，我们要找到向量(u,v,1) 同时与向量 (ABx,ACx,PAx)、(ABy,ACy,PAy)正交。我希望你明白我将要做什么。先给一个提示：要找到平面中两条直线的交点（这正是我们在这里所做的），计算一个交叉乘积就足够了。 顺便说一下，你可以自己测试一下：如何找到通过两个给定点的直线方程。

因此，让我们来编写新的光栅化程序。我们遍历三角形边界框的所有像素。对于每一个像素，计算其重心坐标。如果它至少有一个负的分量，那么像素就在三角形之外。直接看程序可能更清晰：

#include  
#include  
#include "geometry.h"
#include "tgaimage.h" 
 
const int width  = 200; 
const int height = 200; 
 
Vec3f barycentric(Vec2i *pts, Vec2i P) { 
    Vec3f u = cross(Vec3f(pts[2][0]-pts[0][0], pts[1][0]-pts[0][0], pts[0][0]-P[0]), Vec3f(pts[2][1]-pts[0][1], pts[1][1]-pts[0][1], pts[0][1]-P[1]));
    /* `pts` and `P` has integer value as coordinates
       so `abs(u[2])` < 1 means `u[2]` is 0, that means
       triangle is degenerate, in this case return something with negative coordinates */
    if (std::abs(u[2])<1) return Vec3f(-1,1,1);
    return Vec3f(1.f-(u.x+u.y)/u.z, u.y/u.z, u.x/u.z); 
} 
 
void triangle(Vec2i *pts, TGAImage &image, TGAColor color) { 
    Vec2i bboxmin(image.get_width()-1,  image.get_height()-1); 
    Vec2i bboxmax(0, 0); 
    Vec2i clamp(image.get_width()-1, image.get_height()-1); 
    for (int i=0; i<3; i++) { 
        for (int j=0; j<2; j++) { 
            bboxmin[j] = std::max(0,        std::min(bboxmin[j], pts[i][j])); 
            bboxmax[j] = std::min(clamp[j], std::max(bboxmax[j], pts[i][j])); 
        } 
    } 
    Vec2i P; 
    for (P.x=bboxmin.x; P.x<=bboxmax.x; P.x++) { 
        for (P.y=bboxmin.y; P.y<=bboxmax.y; P.y++) { 
            Vec3f bc_screen  = barycentric(pts, P); 
            if (bc_screen.x<0 || bc_screen.y<0 || bc_screen.z<0) continue; 
            image.set(P.x, P.y, color); 
        } 
    } 
} 
 
int main(int argc, char** argv) { 
    TGAImage frame(200, 200, TGAImage::RGB); 
    Vec2i pts[3] = {Vec2i(10,10), Vec2i(100, 30), Vec2i(190, 160)}; 
    triangle(pts, frame, TGAColor(255, 0, 0)); 
    frame.flip_vertically(); // to place the origin in the bottom left corner of the image 
    frame.write_tga_file("framebuffer.tga");
    return 0; 
}

barycentric()方法是用来计算点P在给定三角形的重心坐标，我们已经看到了细节。现在让我们来看triangle()函数是如何工作的。首先，它计算一个边界框，它由左下角和右上角描述。为了找到这两个角，我们遍历三角形的顶点并选择最小/最大坐标。 我还添加了一个带屏幕矩形的边界框裁剪，以节省绘制屏幕外三角形的CPU时间。 恭喜你，你知道如何绘制一个三角形！

平面着色渲染

我们已经知道如何绘制带有空三角形的模型。现在让我们给三角形填充一个随机颜色。这将有助于我们了解填充三角形的编码情况。 这是代码：

for (int i=0; infaces(); i++) { 
    std::vector face = model->face(i); 
    Vec2i screen_coords[3]; 
    for (int j=0; j<3; j++) { 
        Vec3f world_coords = model->vert(face[j]); 
        screen_coords[j] = Vec2i((world_coords.x+1.)*width/2., (world_coords.y+1.)*height/2.); 
    } 
    triangle(screen_coords[0], screen_coords[1], screen_coords[2], image, TGAColor(rand()%255, rand()%255, rand()%255, 255)); 
}

很简单，就像以前一样，我们遍历所有的三角形，将世界坐标转换到屏幕坐标，然后绘制它。我将在接下来的文章中详细描述不同的坐标系。当前渲染的图片看起来是这样的：

为了避免这些小丑般的颜色，我们加入一些光照。首先需要明确：“在光照强度一样的地方，多边形与光线方向正交的时候被照得最亮"。让我们对比一下：

如果多边形与光照方向平行，那么光照亮度为零。换句话说：照明强度等于光矢量和给定三角形的法线的标量积。 三角形的法线可以简单地通过两边的叉积计算得到。

旁注：在本课程中，我们对颜色进行线性计算。 然而（128,128,128）颜色并不是（255,255,255）亮度的一半。 我们将忽略伽马校正并容忍我们颜色亮度的不正确。

for (int i=0; infaces(); i++) { 
    std::vector face = model->face(i); 
    Vec2i screen_coords[3]; 
    Vec3f world_coords[3]; 
    for (int j=0; j<3; j++) { 
        Vec3f v = model->vert(face[j]); 
        screen_coords[j] = Vec2i((v.x+1.)*width/2., (v.y+1.)*height/2.); 
        world_coords[j]  = v; 
    } 
    Vec3f n = (world_coords[2]-world_coords[0])^(world_coords[1]-world_coords[0]); 
    n.normalize(); 
    float intensity = n*light_dir; 
    if (intensity>0) { 
        triangle(screen_coords[0], screen_coords[1], screen_coords[2], image, TGAColor(intensity*255, intensity*255, intensity*255, 255)); 
    } 
}

但点积可能是负数。 这是什么意思？ 这意味着光线来自多边形后面。 如果场景建模得很好（通常是这种情况），我们可以简单地丢弃这个三角形。 这允许我们快速删除一些不可见的三角形。 它被称为背面剔除。

注意，嘴的内腔被绘制在嘴唇的顶部。 这是因为我们对不可见三角形的剪裁手段还比较差：它仅适用于凸形。 下次当我们使用z缓冲区编码之后，我们就会避免这一现象。

这是渲染的当前版本。 你觉得我脸上的形象更加细致吗？ 好吧，因为我作弊了一下：我的脸部模型有25万个三角形，而这个人造头模型大约有一千个。 但我的脸确实是用上面的代码渲染的。 我保证，在下面的文章中我们将为此图片添加更多细节。

 

感谢原作者Dmitry V. Sokolov的授权，原文链接：https://github.com/ssloy/tinyrenderer/wiki/Lesson-2:-Triangle-rasterization-and-back-face-culling